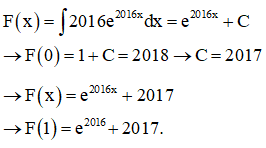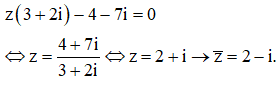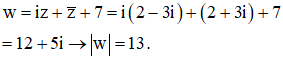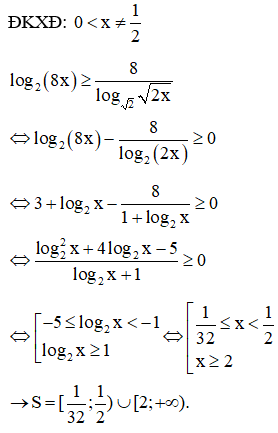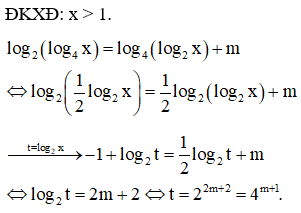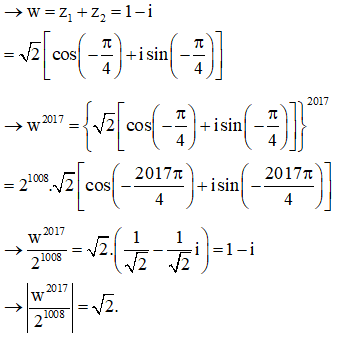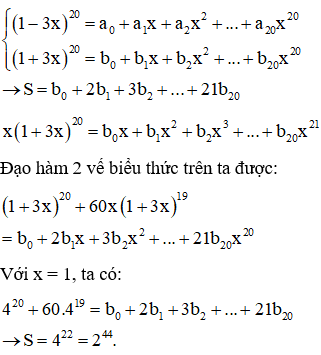50 câu hỏi trắc nghiệm thuộc Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 13

Câu 1:

Cho 10 điểm phân biệt. Hỏi có thể tạo ra bao nhiêu vectơ có điểm đầu và điểm cuối không trùng nhau được lấy từ 10 điểm trên?

A. $C_{10}^{2} .$

B. $A_{10}^{2} .$

C. 20

D. $2^{10}$

Xem đáp án

Đáp án B.

Từ 2 điểm phân biệt có thể tạo được 2 vecto nên số vecto tạo ra được là $A_{10}^{2} .$

Câu 2:

Cho hàm số y = f(x) xác định, liên tục trên đoạn [a;b] (a < b) và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) có bao nhiêu điểm cực trị?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án B.

Câu 3:

Trong các hàm số sau, đâu là hàm số đồng biến trên R?

A. $y = 0, 5^{x} .$

B. $y = {(\frac{π}{4})}^{x} .$

C. $y = 3^{- x} .$

D. $y = 2^{x} .$

Xem đáp án

Đáp án D.

Câu 4:

Với các số thực dương a,b bất kì. Mệnh đề nào dưới đây đúng?

A. $\log (a + b) = \log a . \log b .$

B. $\log a^{b} = \frac{1}{b} \log a .$

C. $\log \frac{a}{b} = \log a - \log b .$

D. $\log a + \log b = \log (a + b) .$

Xem đáp án

Đáp án C.

Câu 5:

Trong các đẳng thức sau, đẳng thức nào sai?

A. $\int \frac{d x}{a x + b} = \frac{1}{a} \ln |a x + b| + C (a \neq 0) .$

B. $\int \frac{d x}{\sin^{2} x} = \cot x + C .$

C. $\int e^{x} d x = e^{x} + C .$

D. $\int d x = x + C .$

Xem đáp án

Đáp án B.

$\int \frac{d x}{\sin^{2} x} = - \cot x + C .$

Câu 6:

Cho số phức z = 2 - 3i. Phần ảo của số thức $\bar{\bar{z}}$ là?

A. 3

B. 2

C. -3

D. -2

Xem đáp án

Đáp án A.

$Z = 2 - 3 i \to \bar{z} = 2 + 3 i .$

Câu 7:

Cho hình nón có bán kính đáy là r và độ dài đường sinh là l. Diện tích xung quanh $S_{x q}$ của hình nón bằng bao nhiêu?

A. $S_{x q} = π r (l + r) .$

B. $S_{x q} = 2 π r l .$

C. $S_{x q} = π r l .$

D. $S_{x q} = 2 π r (l + r) .$

Xem đáp án

Đáp án C.

Câu 8:

Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có $A (1; - 1; 0), B (2; 3; 1), C (3; 1; - 4)$ . Tọa độ tâm G của tam giác ABC là

A. G(6;3;-3)

B. G(4;2;-2)

C. G(-2;-1;1)

D. G(2;1;-1)

Xem đáp án

Đáp án D.

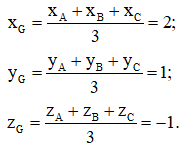
Câu 9:

Đồ thị của hàm số $y = x^{3} + 3 x^{2} - 3$ và đồ thị của hàm số $y = x^{2} - 2 x - 3$ có tất cả bao nhiêu điểm chung?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Đáp án C.

Xét phương trình hoành độ giao điểm của 2 đồ thị:

Câu 10:

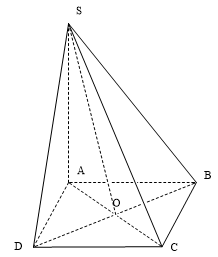
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?

A. $S A ⊥ B D .$

B. $S C ⊥ B D .$

C. $A D ⊥ S C .$

D. $S O ⊥ B D .$

Xem đáp án

Đáp án C.

Câu 11:

Cho hàm số y = f(x) xác định trên R\{2}, liên tục trên mỗi khoảng và có bảng biến thiên như sau

Tập hợp tất cả các số thực m sao cho phương trình f(x) = m có hai nghiệm thực phân biệt là

A. $(- \infty; 1) .$

B. {3}

C. $(- \infty; 1] \cup \{3\} .$

D. $(- \infty; 1] .$

Xem đáp án

Đáp án C.

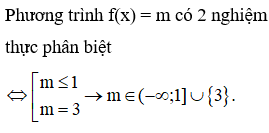
Câu 12:

Cho bốn số -3; a; b; 15 theo thứ tự tạo thành cấp số cộng. Tính giá trị của $T = a^{2} + b^{2} .$

A. T = 84.

B. T = 144.

C. T = 12.

D. T = 90.

Xem đáp án

Đáp án D.

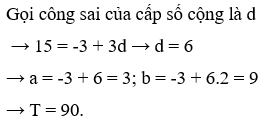
Câu 13:

Cho biểu thức $P = \sqrt{x . \sqrt[3]{x^{2} . \sqrt[4]{x^{3}}}}$ với x > 0. Biết viết gọn P ta được $P = x^{\frac{m}{n}} v ớ i \frac{m}{n}$ là phân số tối giãn (m, n > 0). Hỏi tổng m + n bằng bao nhiêu?

A. 45.

B. 47.

C. 46.

D.48.

Xem đáp án

Đáp án B.

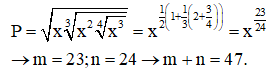
Câu 14:

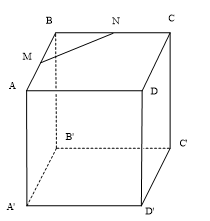
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AB, BC. Tính góc của cặp đường thẳng MN và C’D’

A. 30º.

B. 45º.

C. 60º.

D. 90º

Xem đáp án

Đáp án B.

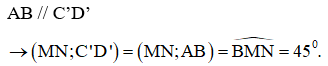
Câu 15:

Cho hàm số f(x) có đạo hàm trên đoạn [1,3], f(1) = 1 và f(3) = 2018. Giá trị của tích phân $I = \int_{1}^{3} f' (x) d x$ là

A. I = 2017.

B. I = -2017.

C. I = 2018.

D. I = 2016.

Xem đáp án

Đáp án A.

Câu 16:

Biết F(x) làm một nguyên hàm của hàm số $f (x) = 2016 e^{2016 x} v à F (0) = 2018$ . Giá trị của F(1) là

A. $F (1) = 2016.$

B. $F (1) = 2016 e^{2016} .$

C. $F (1) = 2016 e^{2016} + 2.$

D. $F (1) = e^{2016} + 2017.$

Xem đáp án

Đáp án D.

Câu 17:

Cho số phức $z (3 + 2 i) - 4 - 7 i = 0$ . Tổng phần thực và phần ảo của z là

A. 3

B. -1

C. 1

D. 2

Xem đáp án

Đáp án C.

Câu 18:

Cho số phức z = 2 - 3i. Môđun của số phức $w = i z + \bar{z} + 7$ bằng bao nhiêu?

A. |w| = 17

B. |w| = 5

C. |w| = 13

D. |w| = 10

Xem đáp án

Đáp án C.

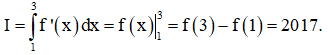
Câu 19:

Cho hình chóp S.ABCD có thể tích bằng 36 và G là trọng tâm tam giác SBC. Thể tích V của khối chóp G.ABCD là

A. V = 18.

B. V = 9.

C. V = 6.

D. V =12.

Xem đáp án

Đáp án D.

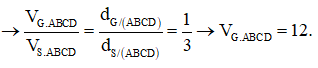
Câu 20:

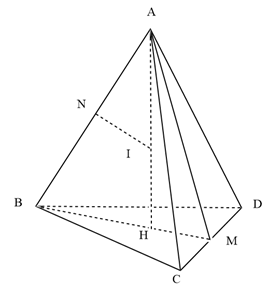
Bán kính của mặt cầu ngoại tiếp tứ diện đều cạnh a là

A. $\frac{a \sqrt{3}}{4} .$

B. $\frac{a \sqrt{6}}{4} .$

C. $\frac{a}{2}$

D. $\frac{2 a}{3}$

Xem đáp án

Đáp án B.

M là trung điểm của CD; N là trung điểm của AB.

Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD.

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho A(1;2;0) và mặt phẳng $(P) : 2 x - y + 2 z - 6 = 0$ . Mặt cầu tâm A tiếp xúc với (P) có phương trình là

A. ${(x + 1)}^{2} + {(y + 2)}^{2} + z^{2} = 2.$

B. ${(x + 1)}^{2} + {(y + 2)}^{2} + z^{2} = 4.$

C. ${(x - 1)}^{2} + {(y - 2)}^{2} + z^{2} = 2.$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + z^{2} = 4.$

Xem đáp án

Đáp án D.

Mặt cầu tâm A, tiếp xúc (P) có bán kính:

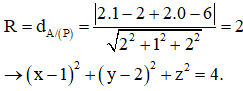
Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho $Δ_{1} : \frac{x - 1}{2} = \frac{y}{1} = \frac{z + 2}{- 1} v à Δ_{2} : \frac{x}{1} = \frac{y + 2}{- 2} = \frac{z - 3}{3} .$ Mặt phẳng (α) chứa $Δ_{1}$ và song song với $Δ_{2}$ có phương trình là

A. $x - 7 y - 5 z - 11 = 0.$

B. $x + 7 y - 5 z + 11 = 0.$

C. $2 x + 3 y + 7 z + 12 = 0.$

D. $2 x - 3 y + z = 0.$

Xem đáp án

Đáp án A.

Câu 23:

Gọi a, b lần lượt là nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình $\frac{1 - \cos 2 x}{2 (1 - \cos x)} + \sqrt{3} \sin x = 3.$ Tình tổng T = a + b.

A. $T = \frac{π}{3} .$

B. $T = - \frac{4 π}{3} .$

C. $T = - \frac{π}{3} .$

D. $T = - \frac{5 π}{3} .$

Xem đáp án

Đáp án B.

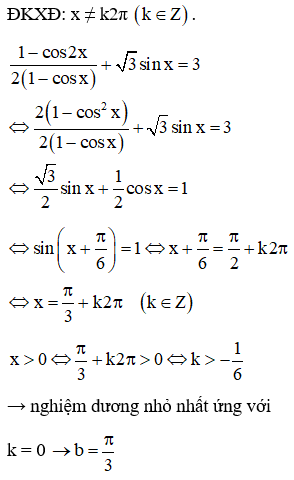
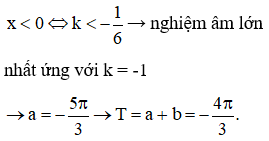
Câu 24:

Tất cả các giá trị thực của m để hàm số $y = m x^{4} + (m - 1) x^{2} + 2$ có đúng một cực đại và không có cực tiểu

A. $m \leq 0.$

B. $m \leq 0$ hoặc $m \geq 1.$

C. $m \geq 1.$

D. m < 0

Xem đáp án

Đáp án A.

Câu 25:

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{x + 1}{x^{2} + x + 1}$ . Giá trị của M - 3m bằng bao nhiêu?

A. 0

B. 1

C. -1

D. 2

Xem đáp án

Đáp án D.

Câu 26:

Cho hàm số $y = \frac{x + 2}{x - 1}$ có đồ thị (C). Biết $M (x_{0}; y_{0})$ thuộc (C) $(x_{0} < 0)$ và khoảng cách từ M t $\sqrt{2}$ ới đường thẳng $∆$ bằng với $Δ : y = - x$ . Khi đó $x_{0} - y_{0}$ bằng

A. 1

B. -1

C. 2

D. -2

Xem đáp án

Đáp án D.

Câu 27:

Tập nghiệm S của bất phương trình $\log_{2} (8 x) \geq \frac{8}{\log_{\sqrt{2}} \sqrt{2 x}}$ là

A. $S = [\frac{1}{32}; \frac{1}{2}) \cup [2; + \infty) .$

B. $S = (- \infty; \frac{1}{32}] \cup [\frac{1}{2}; 2] .$

C. $S = (- \infty; \frac{1}{32}] \cup (\frac{1}{2}; 2] .$

D. $S = [\frac{1}{32}; \frac{1}{2}] \cup [2; + \infty) .$

Xem đáp án

Đáp án A.

Câu 28:

Số thực x thỏa mãn $\log_{2} (\log_{4} x) = \log_{4} (\log_{2} x) + m (m \in ℝ)$ thì giá trị $\log_{2} x$ bằng

A. $4^{m + 1} .$

B. $2^{m + 1} .$

C. $2^{m}$

D. $2^{4^{m + 1}} .$

Xem đáp án

Đáp án A.

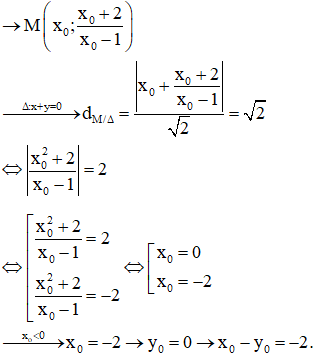
Câu 29:

Có tất cả bao nhiêu giá trị nguyên của m để hàm số $f (x) = \{\begin{cases} \frac{8 (\sqrt{3 x + 1} - 2)}{x^{2} - 1} k h i x > 1 \\ m^{3} x^{2} - (m - 3) x k h i x \leq 1 \end{cases}$ có giới hạn tại x = 1.

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án C.

Câu 30:

Phương trình $4^{x^{2}} - 2^{x^{2} + 2} + 6 = m$ có ba nghiệm thực phân biệt khi và chỉ khi

A. $m \geq 3.$

B. 2 < m < 3

C. m = 2

D. m = 3

Xem đáp án

Đáp án D.

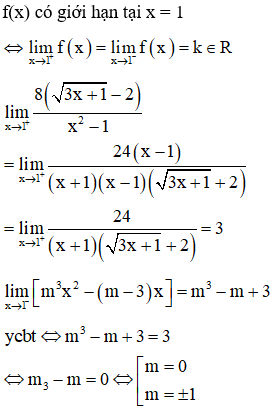
Câu 31:

Cho hình phẳng (H) giới hạn bới các đường $y = \sqrt{3 x + 1}, y = x - 1$ và $x = 1$ . Diện tích S của hình phẳng (H) là

A. $S = \frac{4}{3} .$

B. $S = \frac{40}{9} .$

C. $S = \frac{9}{40} .$

D. $S = \frac{3}{4} .$

Xem đáp án

Đáp án B.

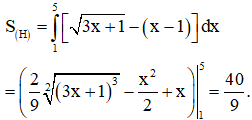
Câu 32:

Cho hình phẳng (H) giới hạn bởi các đường $y = \sin x, x = \frac{π}{2}$ , hai trục tọa độ. Thể tích V của khối tròn xoay khi quay (H) quanh trục Ox là

A. $V = \frac{π}{2} .$

B. $V = \frac{π^{2}}{4} .$

C. $V = \frac{π (π + 1)}{4} .$

D. $V = \frac{π}{3} .$

Xem đáp án

Đáp án B.

Câu 33:

Cho số phức $z_{1} = 1 - 2 i v à z_{2} = i$ . Biết $w = z_{1} + z_{2}$ . Môđun của số phức $\frac{w^{2017}}{2^{1008}}$ là

A. $\frac{\sqrt{2}}{2} .$

B. $\sqrt{2}$

C. 1

D. 2

Xem đáp án

Đáp án B.

Câu 34:

Trong các kết luận sau, kết luận nào sai?

A. Môđun của số phức z là một số thực.

B. Môđun của số phức z là một số thực không âm.

C. Môđun của số phức z là một số phức.

D. Môđun của số phức z là một số thực dương.

Xem đáp án

Đáp án D

Câu 35:

Cho khối trụ có chiều cao h = 3 và diện tích toàn phần bằng $20 π$ . Khi đó chu vi đáy của khối trụ là

A. $2 π$

B. $4 π$

C. $6 π$

D. $8 π$

Xem đáp án

Đáp án B.

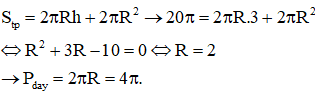
Câu 36:

Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2a, khoảng cách từ A đến mặt phẳng (A'BC) bằng $v$ Thể tích của khối lăng trụ đã cho bằng

A. $3 a^{3}$

B. $a^{3}$

C. $\frac{4 \sqrt{3} a^{3}}{3} .$

D. $\frac{3 a^{3}}{4} .$

Xem đáp án

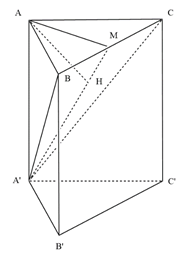
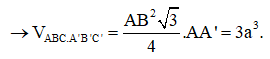
Đáp án A.

Câu 37:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a. Hình chiếu vuông góc của A trên mặt phẳng (ABCD) là trung điểm H của AB. Diện tích tam giác SAB bằng $a^{2}$ . Thể tích V của khối chóp S.HCD là

A. $V = \frac{3 a^{3}}{2} .$

B. $V = \frac{a^{3}}{2} .$

C. $V = a^{3} .$

D. $V = \frac{a^{3}}{3} .$

Xem đáp án

Đáp án B.

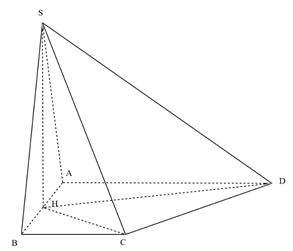
SH vuông góc với AB tại trung điểm của AB nên ΔSAB cân tại A.

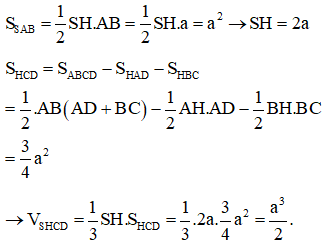
Câu 38:

rong không gian với hệ tọa độ Oxzy, cho đường thẳng $d_{1} : \frac{x - 1}{a} = \frac{y - 3}{b} = \frac{z}{4} v à d_{2} : \frac{x}{1} = \frac{y + 1}{4} = \frac{z - 2}{- 2}$ . Tổng a + b bằng bao nhiêu để d₁//d₂?

A. a + b = -10

B. a + b = 10

C. a + b = 6

D. không tồn tại

Xem đáp án

Đáp án D.

d₁) đi qua điểm M₁(1;3;0), có vecto chỉ phương là ${\vec{u}}_{1} = (a; b; 4)$

(d₂) đi qua điểm M₂(0;-1;2), có vecto chỉ phương là ${\vec{u}}_{2} = (1; 4; - 2)$

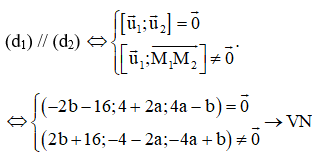
Câu 39:

Trong không gian với hệ tọa độ O_xyz_, cho $A (0; 3; 0), B (0; 0; - 1)$ và C thuộc tia Ox Biết khoảng cách từ C tới mặt phẳng $(P) : 2 x - y + 2 z + 1 = 0$ bằng 1. Mặt phẳng (ABC) có phương trình là?

A. $3 x + y - 3 z - 3 = 0.$

B. $3 x - y + 3 z + 3 = 0.$

C. $x + y - 3 z - 3 = 0.$

D. $x - y + 3 z + 3 = 0.$

Xem đáp án

Đáp án A.

Câu 40:

Trong mặt phẳng tọa độ Oxy. Ở các góc phần tư thứ I, thứ II, thứ III, thứ IV ta lần lượt lấy 1, 2, 3 và 4 điểm phân biệt (các điểm không nằm trên các trục tọa độ và ba điểm bất kì không thẳng hàng). Ta lấy 3 điểm bất kì trong 10 điểm trên. Tính xác suất để 3 điểm đó tạo thành tam giác có 2 cạnh đều cắt trục tọa độ.

A. $\frac{5}{6} .$

B. $\frac{2}{5} .$

C. $\frac{13}{24} .$

D. $\frac{15}{29} .$

Xem đáp án

Đáp án C.

- Tam giác ABC tạo thành có 2 cạnh cắt trục tọa độ khi B; C thuộc 1 góc phần tư, A thuộc góc phần tư khác:

Câu 41:

Đường cong trong hình bên là đồ thị của hàm số f(x). Biết F(x) là một nguyên hàm của f(x) và F(x) là một trong bốn đồ thị dưới đây

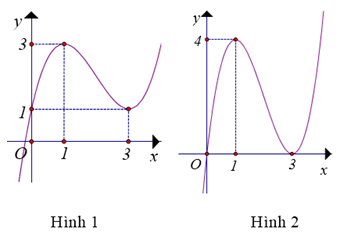
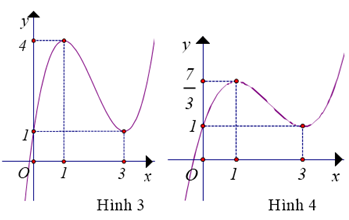
Hỏi F(x) là đồ thị thuộc hình nào?

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Xem đáp án

Đáp án D.

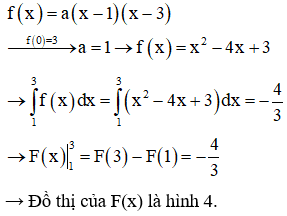
Câu 42:

Có bao nhiêu giá trị nguyên của m để phương trình $m \sqrt{x^{2} + 2} = x + m$ có hai nghiệm thực phân biệt?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án A.

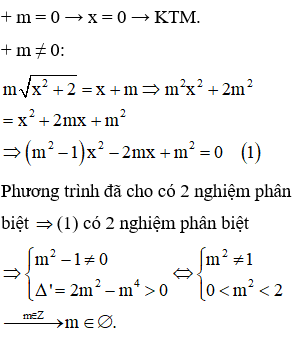
Câu 43:

Tất cả các giá trị thực của m để phương trình $2^{x^{2} - 2 |x + m|} = \log_{x^{2} + 2} (2 |x + m| + 2)$ có nghiệm là

A. $m \geq - \frac{1}{2} .$

B. $m \leq \frac{1}{2} .$

C. $m = \frac{1}{2} .$

D. $m \in ℝ .$

Xem đáp án

Đáp án D.

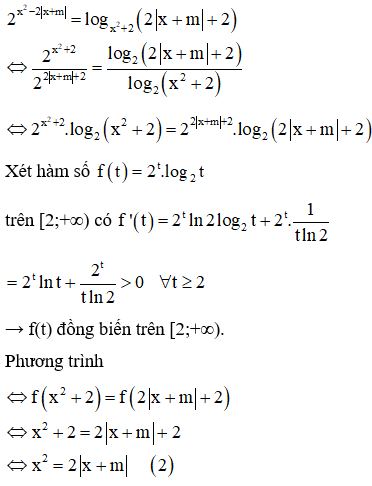
Phương trình (2) có nghiệm với mọi m nên phương trình đã cho có nghiệm với mọi m.

Câu 44:

Cho hình phẳng (H) giới hạn bởi các đường $y = x \sqrt{x^{2} + 1}, x = \sqrt{3}$ và hai trục tọa độ. Đường thẳng $x = k (0 < k < \sqrt{3})$ chia (H) thành hai phần có diện tích S₁, S₂ như hình vẽ bên. Để $S_{1} = 6 S_{2} t h ì k = k_{0}$ . Hỏi $k_{0}$ gần giá trị nào nhất trong các giá trị sau?

A. 0,92.

B. 1,24.

C. 1,52.

D. 1,64.

Xem đáp án

Đáp án D.

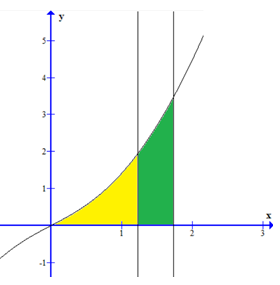
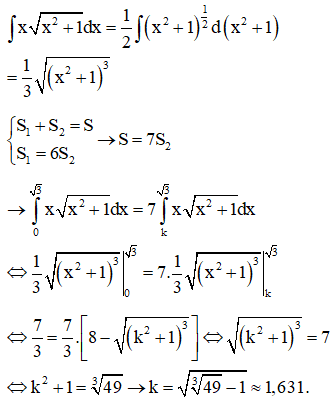
Câu 45:

Cho Parapol $(P) : y = x^{2} + 1$ và đường thẳng $(d) : y = m x + 2$ . Tìm m để diện tích hình phẳng giới hạn bởi (P) và (d) đạt giá trị nhỏ nhất?

A. 0

B. $\frac{3}{4} .$

C. $\frac{4}{3}$

D. 1

Xem đáp án

Đáp án A.

$= (x_{2} - x_{1}) \{- \frac{1}{3} [{(x_{1} + x_{2})}^{2} - x_{1} x_{2}] + \frac{m}{2} (x_{1} + x_{2}) + 1\}$

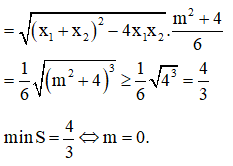
Câu 46:

Cho tam giác ABC có AB = 3a, đường cao CH = a và AH = a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A', B', C' sao cho AA' = 3a, BB' = 2a, CC' = a. Tính diện tích tam giác A'B'C'.

A. $\frac{a^{2} \sqrt{39}}{3} .$

B. $\frac{a^{2} \sqrt{21}}{3} .$

C. $\frac{a^{2} \sqrt{26}}{2} .$

D. $\frac{a^{2} \sqrt{35}}{2} .$

Xem đáp án

Đáp án D.

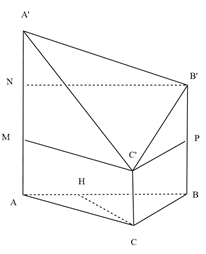
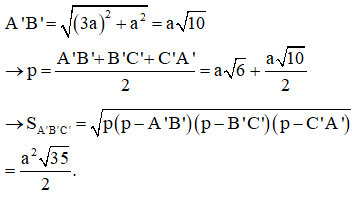
Câu 47:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD) và SA = a. Điểm M thuộc cạnh SA sao cho $\frac{S M}{S A} = k$ . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

A. $k = \frac{- 1 + \sqrt{3}}{2} .$

B. $k = \frac{- 1 + \sqrt{5}}{2} .$

C. $k = \frac{- 1 + \sqrt{2}}{2} .$

D. $k = \frac{1 + \sqrt{5}}{2} .$

Xem đáp án

Đáp án B

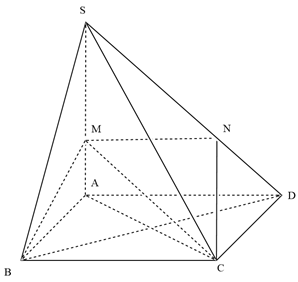
Câu 48:

Cho hình chóp S.ABC có SA = a, $S B + S C = m (m > 2 a)$ . BSC = CSA = ASB = 60º và $∆ A B C$ vuông tại A. Tính thể tích chóp S.ABC theo a và m.

A. $V = \frac{a^{2} (m - a) \sqrt{3}}{12} .$

B. $V = \frac{a^{2} (m - a) \sqrt{2}}{12} .$

C. $V = \frac{a^{2} (m - 2 a) \sqrt{3}}{12} .$

D. $V = \frac{a^{2} (m - 2 a) \sqrt{2}}{12} .$

Xem đáp án

Đáp án D.

Trên các tia SB; SC lần lượt lấy các điểm B’; C’ sao cho SB’ = SC’ = SA = a.

Câu 49:

Khai triển đa thức: ${(1 - 3 x)}^{20} = a_{0} + a_{1} x + a_{2} x^{2} + ... + a_{20} x^{20} .$ Tính tổng:

$S = |a_{0}| + 2 |a_{1}| + 3 |a_{2}| + ... + 21 |a_{20}|$

A. $S = 2^{44} .$

B. $S = 4^{23} .$

C. $S = 3^{20} .$

D. $S = 5^{18} .$

Xem đáp án

Đáp án A.

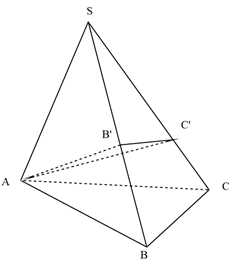
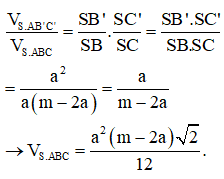
Câu 50:

Trong không gian với hệ trục tọa độ Oxyz. Mặt phẳng (P) đi qua điểm M(1;27;8) cắt các tia Ox,Oy, Oz lần lượt tại A, B, C sao cho $A B^{2} + B C^{2} + C A^{2}$ nhỏ nhất có phương trình là

A. $6 x + 2 y + 3 z - 84 = 0.$

B. $6 x - 2 y + 3 z + 24 = 0.$

C. $6 x - 2 y - 3 z + 72 = 0.$

D. $6 x + 2 y - 3 z - 36 = 0.$

Xem đáp án

Đáp án A.

Gọi A(a;0;0); B(0;b;0); C(0;0;c) (a; b; c > 0)

→ Phương trình mặt phẳng (P) là

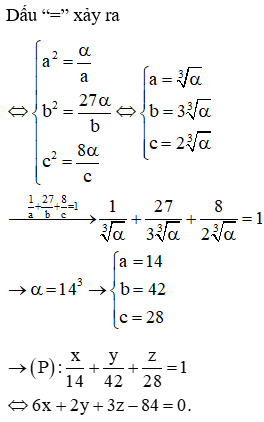
* PS: do a; b; c > 0 nên chỉ có đáp án A thỏa mãn.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 13

Danh sách câu hỏi

Bài thi liên quan