25 câu hỏi trắc nghiệm thuộc Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 17

Câu 1:

Trong các dãy số sau, có bao nhiêu dãy là cấp số cộng:

a) Dãy số $(u_{n})$ với $u_{n} = 3 n$

b) Dãy số $(v_{n})$ với $v_{n} = \sin n π$

c) Dãy số $(w_{n})$ với , với $w_{n} = \frac{n}{5} - 2$ , với $n \leq 10$

d) Dãy số $(t_{n})$ với $t_{n} = \sqrt{2} - n$

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án D

Các dãy số (hữu hạn hoặc vô hạn) với số hạng tổng quát có dạng an+b ( a, b là hằng số) đều là một cấp số cộng với công sai d = a

Câu 2:

Cho hàm số $f (x) = \frac{1}{x^{2}}$ . Hỏi đồ thị (C) của hàm số $y = f' (x)$ đi qua điểm nào sau đây:

A. M(1;2)

B. N(-1;1)

C. P(1;-1)

D. Q(-1;2)

Xem đáp án

Đáp án D

Câu 3:

Hàm số nào sau đây nghịch biến trên từng khoảng xác định?

A. $y = x^{4} - x^{2}$

B. $y = - x^{3} + 3 x^{2}$

C. $y = 2 x - sinx$

D. $y = \frac{x - 1}{x - 2}$

Xem đáp án

Đáp án D

Câu 4:

Cho hàm f có đạo hàm trên R và có $f' (x) = x^{3} {(x - 1)}^{2} {(2 - x)}^{4}$ . Số điểm cực đại của hàm f là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án A

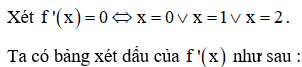
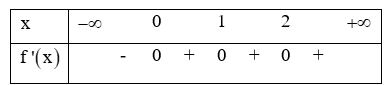
Từ đó, ta thấy rằng hàm số chỉ có đúng một điểm cực trị và đó là điểm cực tiểu.

Câu 5:

Giá trị lớn nhất của hàm số $y = 3 x^{5} - 5 x^{3} + 2$ trên đoạn $[- \frac{3}{2}; \frac{1}{2}]$ là:

A. 4

B. 6

C. 2

D. $\frac{47}{32}$

Xem đáp án

Đáp án A

Câu 6:

Cho khối chóp có đáy là tam giác đều. Nếu tăng độ dài của ba cạnh đáy lên m lần và giảm độ dài chiều cao m lần thì thể tích khối chóp khi đó sẽ thay đổi như thế nào so với ban đầu ?

A. tăng m lần

B. $t ă n g m^{2} l ầ n$

C. $g i ả m m^{2} l ầ n$

D. không thay đổi

Xem đáp án

Đáp án A

Câu 7:

Một khối lăng trụ tam giác có cạnh đáy lần lượt là 6cm , 8cm và 10cm , cạnh bên 14cm và góc giữa cạnh bên và mặt đáy bằng $30 °$ . Tính thể tích của khối đó.

A. $112 c m^{3}$

B. $56 \sqrt{3} c m^{3}$

C. $112 \sqrt{3} c m^{3}$

D. $168 c m^{3}$

Xem đáp án

Đáp án D

Giả sử hình lăng trụ là ABC.A’B’C’

Câu 8:

Cho hàm số f(x) xác định, liên tục trên $R \ \{- 1\}$ và có bảng biến thiên như sau.

Tìm tất cả số đường tiệm cận của đồ thị hàm số có bảng biến thiên trên.

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án B

HDG: Dựa vào bảng biến thiên ta có

Câu 9:

Cho hình bát diện đều. Biết rằng các điểm là tâm các mặt của bát diện đều tạo thành một hình đa diện đều. Tên của hình đa diện đó là

A. tứ diện đều

B. lập phương

C. bát diện đều

D. mười hai mặt đều.

Xem đáp án

Đáp án B

Câu 10:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y = \frac{10 - 2 x}{\sqrt{x^{2} + 2 x - 35}}$

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án C

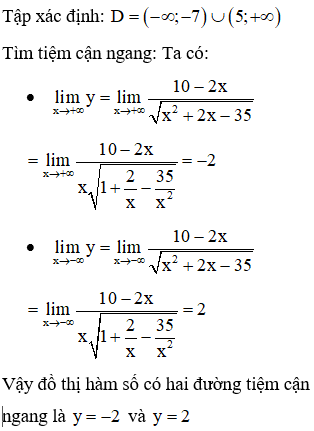
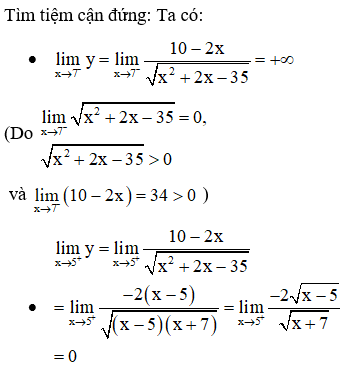
Vậy đồ thị hàm số có một đường tiệm cận đứng là x = -7

Lưu ý: HS có thể sử dụng MTCT để tính nhanh các bài toán tìm lim trên (tuy nhiên nên xem lại cách giải tự luận này khi gặp những bài toán không dùng MTCT được nữa).

Câu 11:

Tìm số giá trị của m để đồ thị hàm số $y = \frac{(m + 3) x - m - 5}{x^{2} - 3 x + m}$ có một đường tiệm cận đi qua điểm A(-1;2)

A. 0

B. 1

C. 2

D. Vô số

Xem đáp án

Đáp án A

hơn bậc mẫu), nên đồ thị hàm số luôn có đúng một tiệm cận ngang là y = 0, với mọi giá trị của m. Tiệm cận ngang này không đi qua điểm A(-1;2)

Vậy ta phải tìm m sao cho đồ thị hàm số có một tiệm cận đứng đi qua điểm A(-1;2), đó là x = 1

Đồ thị hàm số có tiệm cận đứng là x = 1

Câu 12:

Có bao nhiêu điểm M thuộc đồ thị $(C) : y = \frac{x - 2}{x + 2}$ mà tại đó có tiếp tuyến song song với đường thẳng $(d) : x - y - 1 = 0$ ?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

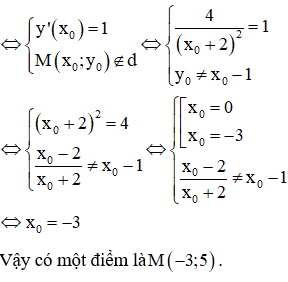
Câu 13:

Gọi $x_{1}; x_{2}$ là hai nghiệm phân biệt của phương trình: $P_{x} . A_{x}^{2} + 72 = 6 (A_{x}^{2} + 2 P_{x})$ . Gọi S là tập hợp tất cả các giá trị của biểu thức $P = C_{7}^{x_{1} + x_{2}} + 2017$ . Tìm tập S.

A. $S = \{2024\}$

B. $S = \{2018; 2024\}$

C. $S = \{2019\}$

D. $S = \{2018\}$

Xem đáp án

Đáp án D

Câu 14:

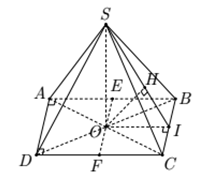
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và $A B = 2 a, B C = a$ . Các cạnh bên của hình chóp bằng nhau và bằng $a \sqrt{2}$ . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a \sqrt{6}}{3}$

C. $\frac{a \sqrt{15}}{5}$

D. $\frac{a \sqrt{21}}{7}$

Xem đáp án

Đáp án D

Câu 15:

Cho hàm số $y = \{\begin{cases} \frac{x^{2} - m x + m^{2} - 3 m}{x - 2}, k h i x \neq 2 \\ 4 m - 1, k h i x = 2 \end{cases}$ . Biết rằng $m = m_{0}$ thì hàm số liên tục tại x = 2 . Giá trị của $P = \sqrt{m_{0}^{4} + 2017}$ gần với giá trị nào nhất sau đây ?

A. 47,68

B. 42,49

C. 44,92

D. 49,42

Xem đáp án

Đáp án C

Câu 16:

Có bao nhiêu giá trị nguyên của tham số $m \in [- 2017; 2017]$ để hàm số $y = \sin^{4} x - \sin^{3} x + \sin^{2} x + m^{2} + 4 m + 3 > 0, \forall x \in R$

A. 4033

B. 4034

C. 2018

D. 4032

Xem đáp án

Đáp án D

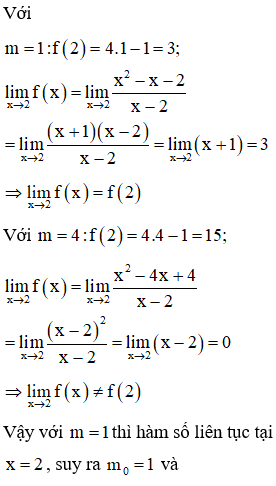
Câu 17:

Cho khối lăng trụ đứng ABC.DEF có đáy là tam giác vuông tại A với $B C = 4 a, ∡ A C B = 60^{0}$ . Biết $∆ B C D$ có chu vi bằng $(9 + \sqrt{17}) a$ . Thể tích khối lăng trụ ABC.DEF là

A. $a^{3} \sqrt{39}$

B. $6 a^{3} \sqrt{39}$

C. $2 a^{3} \sqrt{39}$

D. $26 a^{3} \sqrt{3}$

Xem đáp án

Đáp án C

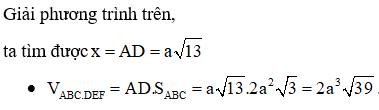
Câu 18:

Có tất cả bao nhiêu giá trị nguyên của tham số thực m để đồ thị của hàm số $y = \frac{x^{3}}{3} - \frac{x^{2}}{2} (m + 2) + 2 m x + 1$ có một điểm cực đại và một điểm cực tiểu đồng thời chúng nằm về cùng một phía so với đường thẳng $(d) : x + y - 1 = 0$

A. 3

B. 4

C. 5

D. 6

Xem đáp án

Đáp án C

Câu 19:

Cho hình chóp S.ABC . có đáy ABC là tam giác vuông tại B . Các mặt bên $(S A C); (S A B)$ cùng vuông góc với đáy, $A C = \frac{\sqrt{13}}{2}; B C = \sqrt{3}; S C = 2$ . Gọilà góc hợp bởi hai mặt phẳng $(S B C); (A B C)$ . Giá trị biểu thức $T = 2 \sin \frac{α}{2} + \frac{2 \sqrt{3}}{3} \cos \frac{α}{2}$

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Câu 20:

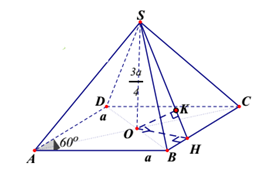
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc $∡ B A D = 60^{0}$ . Đường thẳng SO vuông góc với mặt phẳng đáy $(A B C D) v à S O = \frac{3 a}{4}$ . Khoảng cách từ A đến mặt phẳng (SBC) là:

A. $\frac{a \sqrt{3}}{2}$

B. $\frac{3 a}{2}$

C. $\frac{2 a}{3}$

D. $\frac{3 a}{4}$

Xem đáp án

Đáp án D

Câu 21:

Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho $C K = \frac{2 a}{3}$ . Mặt phẳng $(α)$ qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích $V_{1}, V_{2} (V_{1} < V_{2})$ . Tính tỉ số $\frac{V_{1}}{V_{2}}$

A. $\frac{V_{1}}{V_{2}} = \frac{1}{4}$

B. $\frac{V_{1}}{V_{2}} = \frac{1}{2}$

C. $\frac{V_{1}}{V_{2}} = \frac{2}{3}$

D. $\frac{V_{1}}{V_{2}} = \frac{1}{3}$

Xem đáp án

Đáp án B

Gọi tâm O, O’ lần lượt là tâm của ABCD, A’B’C’D’. Ta có $I = A K \cap O O'$

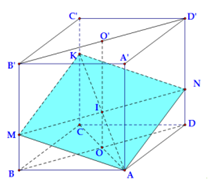
Qua I ta kẻ đường thẳng d song song BD cắt BB', DD' lần lượt tại M, N . Mặt phẳng $(α)$ chính là mặt phẳng (KMAN) chia khối lập phương thành 2 phần.

Ta có 2 phần khối đa diện đối xứng qua (AA'C'C) nên ta chỉ cần xét một nửa thể tích của mỗi phần như sau:

Câu 22:

Gọi M, m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sqrt{2 - x} + 2 \sqrt{2 + x} + 4 \sqrt{4 - x^{2}} + 3 x + 1$ . Tính P = M + m

A. P = 8

B. $P = 8 + 2 \sqrt{5}$

C. $P = 11 + 2 \sqrt{5}$

D. P = 11

Xem đáp án

Đáp án B

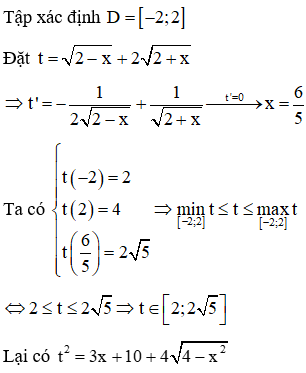
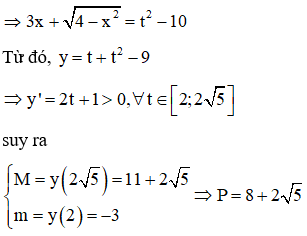
Câu 23:

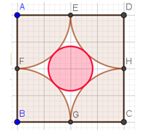
Hai người cùng chơi trò chơi phóng phi tiêu, mỗi người đứng cách một tấm bảng hình vuông ABCD có kích thước là một khoảng cách nhất định. Mỗi người sẽ phóng một cây phi tiêu vào tấm bảng hình vuông ABCD (như hình vẽ). Nếu phi tiêu cắm vào hình tròn tô màu hồng thì người đó sẽ được 10 điểm. Xét phép thử là hai người lần lượt phóng 1 cây phi tiêu vào tấm bảng hình vuông ABCD (phép thử này đảm bảo khi phóng là trúng và dính vào tấm bảng hình vuông, không rơi ra ngoài). Tính xác suất để có đúng một trong hai người phóng phi tiêu được 10 điểm.( kết quả cuối cùng làm tròn số đến 4 chữ số thập phân)

A. 0,2331

B. 0,2330

C. 0,2333

D. 0,2332

Xem đáp án

Đáp án D

Câu 24:

Cho hàm số y = f(x) liên tục trên R và có đồ thị là hình vẽ dưới đây.

Gọi M, m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = {|f (x) - 2|}^{3} - 3 {(f (x) - 2)}^{2} + 5$ trên đoạn [-1;3]. Tính P = Mm .

A. P = 3

B. P = 2

C. P = 54

D. P = 55

Xem đáp án

Đáp án D

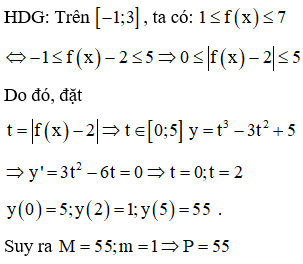
Câu 25:

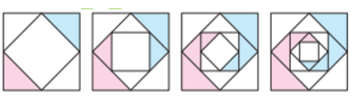
Một thợ thủ công muốn vẽ trang trí trên một hình vuông kích thước 4mx4m, bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu, và tô kín màu lên hai tam giác đối diện ( như hình vẽ). Quá trình vẽ và tô theo qui luật đó được lặp lại 5 lần. Tính số tiền nước sơn để người thợ thủ công đó hoàn thành trang trí hình vuông như trên?. Biết tiền nước sơn để sơn $1 m^{2}$ là 50.000đ.

A. 378500

B. 375000

C. 399609

D. 387500

Xem đáp án

Đáp án D

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 17

Danh sách câu hỏi

Bài thi liên quan