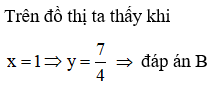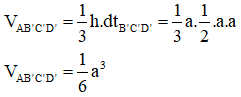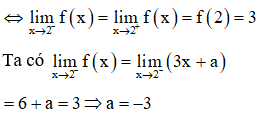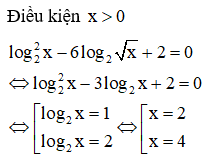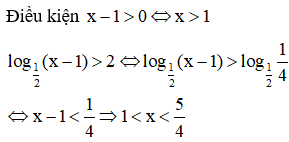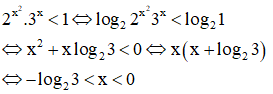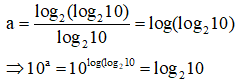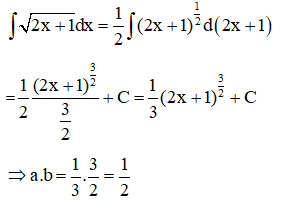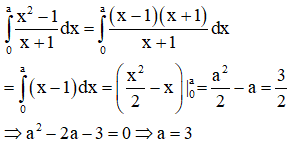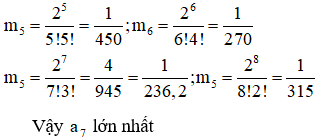50 câu hỏi trắc nghiệm thuộc Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 3

Câu 1:

Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?

A. $y = x^{4} + x^{2} + 1$

B. $y = \frac{x^{4}}{4} + \frac{x^{2}}{2} + 1$

C. $y = x^{3} + x^{2} + 1$

D. $y = x^{2} + x + 1$

Xem đáp án

Đáp án B

Câu 2:

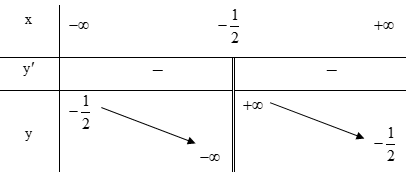
Bảng biến thiên dưới đây là của hàm số nào?

A. $y = \frac{x + 2}{- 2 x - 1}$

B. $y = \frac{- x + 2}{2 x+ 1}$

C. $y = \frac{- x + 2}{2 x - 1}$

D. $y = \frac{x + 2}{2 x+ 1}$

Xem đáp án

Đáp án B

Qua bảng biến thiên ta thấy đồ thị hàm số có tiệm cận đứng

Câu 3:

Tính đạo hàm của hàm số $y = \log_{2} x$ .

A. $y^{'} = \frac{1}{x}$

B. $y^{'} = \frac{\ln 2}{x}$

C. $y^{'} = \frac{1}{x \ln 2}$

D. $y^{'} = \frac{1}{x \log 2}$

Xem đáp án

Đáp án C

Câu 4:

Cho $α$ là số thực dương khác 3. Tính $I = \log_{\frac{3}{a}} (\frac{9}{a^{2}})$ .

A. I = 3

B. $I = \frac{1}{2}$

C. I = 2

D. $I = \frac{1}{a}$

Xem đáp án

Đáp án C

Câu 5:

Tìm nguyên hàm F(x) của hàm số $f (x) = 3 x^{2} - e^{- x}$ thỏa mãn $F (0) = 3$ .

A. $F (x) = x^{3} - e^{- x} - 3$

B. $F (x) = x^{3} + e^{- x} + 2$

C. $F (x) = x^{3} - e^{- x} + 3$

D. $F (x) = x^{3} + e^{- x} - 2$

Xem đáp án

Đáp án B

Câu 6:

Cho hình lập phương $A B C D A^{'} B^{'} C^{'} D^{'}$ cạnh a. Tính thể tích V của khối tứ diện $A B^{'} C^{'} D^{'}$ .

A. $V = \frac{a^{3}}{3}$

B. $V = \frac{a^{3}}{6}$

C. $V = \frac{a^{3}}{2}$

D. $V = \frac{\sqrt{2} a^{3}}{12}$

Xem đáp án

Đáp án B

Câu 7:

Cho hàm số $f (x) = \{\begin{cases} x^{2} - 1, k h i x \geq 2 \\ 3 x + a, k h i x < 2 \end{cases}$ . Tìm a để f(x) liên tục tại $x = 2$

A. a = 3

B. a = 2

C. a = =-3

D. a = -2

Xem đáp án

Đáp án C

Hàm số liên tục tại 2

Câu 8:

Hỏi hàm số $y = - 8 x^{3} + 3 x^{2}$ đồng biến trên khoảng nào?

A. $(- \infty; 0)$

B. $(\frac{1}{4}; + \infty)$

C. $(0; \frac{1}{4})$

D. $(- \infty; \frac{1}{4})$

Xem đáp án

Đáp án C

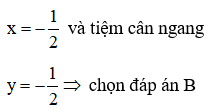
Câu 9:

Tìm số giao điểm của đồ thị hàm số $y = (x - 2) (x^{2} + 3 x + 3)$ với trục hoành.

A. 2

B. 0

C. 1

D. 3

Xem đáp án

Đáp án C

Số giao điểm với trục hoành là số nghiệm của phương trình

Câu 10:

Tìm giá trị lớn nhất của hàm số $y = \frac{4}{x^{2} + 2}$ trên đoạn [-1;1].

A. $\underset{[- 1; 1]}{M a x} y = 2$

B. $\underset{[- 1; 1]}{M a x} y = \frac{4}{3}$

C. $\underset{[- 1; 1]}{M a x} y = \frac{3}{4}$

D. $\underset{[- 1; 1]}{M a x} y = 4$

Xem đáp án

Đáp án A

Câu 11:

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} - 3 x + 2}{x^{2} - 4}$ .

A. x = 2

B. x = -2

C. x = -2, x = 2

D. x = 1

Xem đáp án

Đáp án B

Câu 12:

Cho hàm số $y = x^{4} + a x^{2} + b$ . Tìm a, b để hàm số đạt cực trị tại $x = 1$ và giá trị cực trị bằng $\frac{3}{2}$ .

A. $\{\begin{cases} a = - 2 \\ b = \frac{5}{2} \end{cases}$

B. $\{\begin{cases} a = 2 \\ b = \frac{5}{2} \end{cases}$

C. $\{\begin{cases} a = - 2 \\ b = - \frac{5}{2} \end{cases}$

D. $\{\begin{cases} a = 2 \\ b = \frac{2}{5} \end{cases}$

Xem đáp án

Đáp án A

Câu 13:

Tìm nghiệm của phương trình $\log_{2}^{2} x - 6 \log_{2} \sqrt{x} + 2 = 0$ .

A. $x = - 2, x = 2$

B. x = 2

C. $x = - 4, x = 4$

D. $x = 2, x = 4$

Xem đáp án

Đáp án D

Câu 14:

Giải bất phương trình $\log_{\frac{1}{2}} (x - 1) > 2$ .

A. $1 < x < \frac{5}{4}$

B. $x > \frac{5}{4}$

C. x > 1

D. $x < \frac{5}{4}$

Xem đáp án

Đáp án A

Câu 15:

Tìm nghiệm của bất phương trình $2^{x^{2}} {.3}^{x} < 1$ .

A. $- \log_{2} 3 < x < 0$

B. x > 0

C. $x > - \log_{2} 3$

D. x < 0

Xem đáp án

Đáp án A

Câu 16:

Cho hai số thục dương a và b thỏa mãn $a^{2} + b^{2} = 98 a b$ . Khẳng định nào sau đây là đúng?

A. $2 \log_{2} (a + b) = l o g_{2} a + \log_{2} b$

B. $\log_{2} \frac{a + b}{2} = l o g_{2} a + \log_{2} b$

C. $2 \log_{2} \frac{a + b}{10} = l o g_{2} a + \log_{2} b$

D. $\log_{2} \frac{a + b}{10} = 2 (l o g_{2} a + \log_{2} b)$

Xem đáp án

Đáp án C

Câu 17:

Tính giá trị của biểu thức $P = 10^{a}$ , biết $a = \frac{\log_{2} (\log_{2} 10)}{\log_{2} 10}$ .

A. P = 2

B. P = 4

C. P = 1

D. $P = \log_{2} 10$

Xem đáp án

Đáp án D

Câu 18:

Biết a, b là các số thực thỏa mãn $\int \sqrt{2 x + 1} d x = a {(2 x + 1)}^{b} + C$ . Tính P = ab.

A. $P = - \frac{1}{2}$

B. $P = \frac{3}{2}$

C. $P = \frac{1}{2}$

D. $P = - \frac{3}{2}$

Xem đáp án

Đáp án C

Câu 19:

Cho $\int_{2}^{9} f (x) d x = 6$ . Tính $\int_{0}^{a} \frac{x^{2} - 1}{x + 1} d x = \frac{3}{2}$ .

A. a = 3

B. a = 4

C. a = 5

D. a = 2

Xem đáp án

Đáp án A

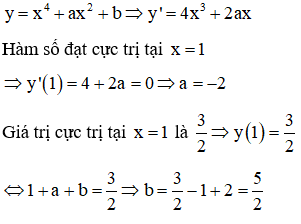
Câu 20:

Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số $y = x^{5} - x^{3}$ và trục hoành.

A. $S = \frac{7}{6}$

B. $S = \frac{17}{6}$

C. $S = \frac{1}{6}$

D. $S = \frac{13}{6}$

Xem đáp án

Đáp án C

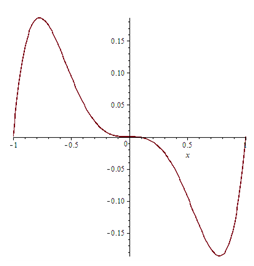
Đồ thị hàm số cắt trục hoành tại 3 điểm có hoành độ lần lượt là -1;0,1.

Diện tích cần tính là

Câu 21:

Cho số phức $z = {(\sqrt{2} + i)}^{2} . (1 - \sqrt{2} i)$ . Tìm phần thực và ảo của số phức $\bar{z}$ .

A. Phần thực bằng 5 và Phần ảo bằng $\sqrt{2}$ .

B. Phần thực bằng 5 và Phần ảo bằng - $\sqrt{2}$ .

C. Phần thực bằng –5 và Phần ảo bằng $\sqrt{2}$ .

D. Phần thực bằng –5 và Phần ảo bằng - $\sqrt{2}$ .

Xem đáp án

Đáp án B

Câu 22:

Gọi $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $- 3 z^{2} + 2 z - 1 = 0$ . Tính $P = \frac{1}{z_{1}} + \frac{1}{z_{2}}$ .

A. P = 9

B. P = 2

C. P = 3

D. P = 10

Xem đáp án

Đáp án B

Câu 23:

Gọi $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $- 3 z^{2} + 2 z - 1 = 0$ . Tính $P = \frac{1}{z_{1}} + \frac{1}{z_{2}}$ .

A. P = 9

B. P = 2

C. P = 3

D. P = 10

Xem đáp án

Đáp án B

Câu 24:

Tìm tất cả các số thực x, y sao cho $1 - x^{2} - y i = i^{3} - i^{2} - i$ .

A. $x = \sqrt{2}, y = 2$

B. $x = 0, y = 2$

C. $x = - \sqrt{2}, y = 2$

D. $x = 2, y = 0$

Xem đáp án

Đáp án B

Câu 25:

Cho số phức z thỏa mãn $(3 + i) z = 13 - 9 i$ . Tìm tọa độ của điểm M biểu diễn z.

A. $M = (- 3; 4)$

B. $M = (3; - 4)$

C. $M = (- 3; - 4)$

D. $M = (1; - 3)$

Xem đáp án

Đáp án B

Câu 26:

Cho hai số phức $z_{1} = 1 + 2 i, z_{2} = 3 - 2 i$ . Tính mô đun của số phức $z_{1} - 2 z_{2}$ .

A. $|z_{1} - 2 z_{2}| = \sqrt{61}$

B. $|z_{1} - 2 z_{2}| = \sqrt{71}$

C. $|z_{1} - 2 z_{2}| = \sqrt{17}$

D. $|z_{1} - 2 z_{2}| = 4$

Xem đáp án

Đáp án A

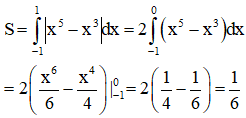
Câu 27:

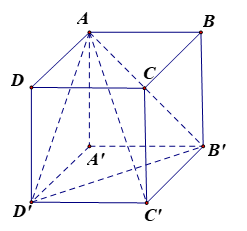
Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa SC và AD bằng $60 °$ . Tính thể tích V của khối chóp SABCD.

A. $V = \frac{\sqrt{2} . a^{3}}{3}$

B. $V = \frac{\sqrt{3} . a^{3}}{3}$

C. $V = \frac{\sqrt{2} . a^{3}}{6}$

D. $V = \frac{2 \sqrt{2} . a^{3}}{3}$

Xem đáp án

Đáp án A

Câu 28:

Cho hình chóp S.ABC có $A C = S C = a, S A = \frac{a \sqrt{3}}{2}$ . Biết thể tích của khối chóp S.ABC bằng $\frac{a^{3} . \sqrt{3}}{16}$ . Tính khoảng cách h từ điểm B tới mặt phẳng (SAC).

A. $h = \frac{a}{\sqrt{13}}$

B. $h = \frac{a}{\sqrt{31}}$

C. $h = \frac{2 a}{\sqrt{13}}$

D. $h = \frac{3 a}{\sqrt{13}}$

Xem đáp án

Đáp án D

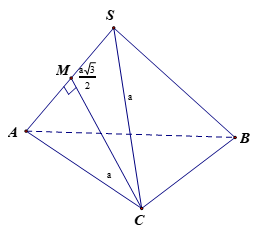
Câu 29:

Cho hình nón có độ dài đường sinh bằng 4, góc giữa đường sinh và mặt đáy bằng $30 °$ . Tính diện tích toàn phần $S_{t p}$ của hình nón.

A. $S_{t p} = (8 \sqrt{3} + 12) π$

B. $S_{t p} = (5 \sqrt{3} + 12) π$

C. $S_{t p} = (8 \sqrt{3} + 2) π$

D. $S_{t p} = (\sqrt{3} + 12) π$

Xem đáp án

Đáp án A

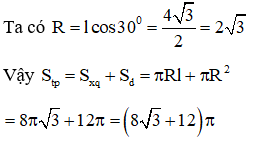
Câu 30:

Cho hình lăng trụ đều $A B C A^{'} B^{'} C^{'}$ có tất cả các cạnh bằng a. Tính diện tích xung quanh $S_{x q}$ của mặt cầu ngoại tiếp hình lăng trụ.

A. $S_{x q} = \frac{π a^{2}}{3}$

B. $S_{x q} = \frac{π a^{2}}{7}$

C. $S_{x q} = \frac{3 π a^{2}}{7}$

D. $S_{x q} = \frac{7 π a^{2}}{3}$

Xem đáp án

Đáp án D

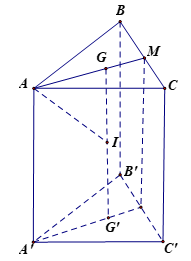
Tâm của mặt cầu là trung điểm I của GG’ với

G,G’ là trọng tâm của các mặt đáy.

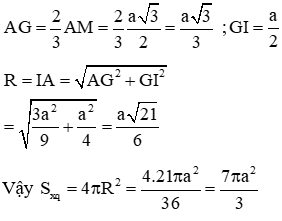
Câu 31:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (1; 2; 3), B (- 2; 1; 5)$ . Véctơ nào dưới đây là véctơ pháp tuyến của mặt phẳng (OAB).

A. $\vec{n} = (7; 8; 5)$

B. $\vec{n} = (- 3; - 2; 1)$

C. $\vec{n} = (- 1; 3; 8)$

D. $\vec{n} = (7; - 11; 5)$

Xem đáp án

Đáp án D

Câu 32:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 2}{1} = \frac{y}{- 1} = \frac{z + 1}{- 2}$ và mặt phẳng . Tìm m để d vuông góc với (P).

A. m = 1

B. m = -1

C. m = 3

D. m = -3

Xem đáp án

Đáp án A

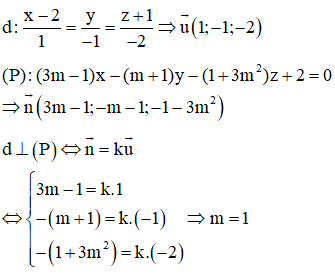
Câu 33:

Trong không gian với hệ tọa độ Oxyz, cho điểm $A (1; 2; 3)$ và cho đường thẳng d có phương trình $\frac{x - 2}{2} = \frac{y + 2}{- 1} = \frac{z - 3}{1}$ . Tìm tọa độ hình chiếu vuông góc H của A trên d.

A. H(0;1;2)

B. H(0;-1;2)

C. H(1;1;1)

D. H(-3;1;4)

Xem đáp án

Đáp án B

Câu 34:

Gọi d là đường thẳng đi qua điểm A(-2;-1;1) và song song với mặt phẳng $(P) : 2 x + y + z - 5 = 0$ , cắt trục tung tại điểm B. Tìm tọa độ của B.

A. B(0;4;0)

B. B(0;-2;0)

C. B(0;2;0)

D. B(0;-4;0)

Xem đáp án

Đáp án D

Câu 35:

Gọi S là tập hợp tất cả các số tự nhiên gồm 3 chữ số phân biệt được chọn từ các chữ số 1, 2, 3, 4, 5, 6, 7. Chọn ngẫu nhiên 1 số từ S, gọi P là xác suất chọn được số chẵn, mệnh đề nào dưới đây đúng?

A. $P = \frac{2}{7}$

B. $P = \frac{3}{5}$

C. $P = \frac{2}{5}$

D. $P = \frac{3}{7}$

Xem đáp án

Đáp án D

Ta thu được số chẵn khi chữ số hàng đơn vị là chắn. Do vai trò của 7 số trong đó có 3 số chẵn là như nhau nên xác suất cần tính bằng $\frac{3}{7}$

Câu 36:

Tìm nghiệm của phương trình $\sin 2 x + 2 \cos 2 x + 4 \cos x - \sin x - 1 = 0$ .

A. $x = \pm \frac{π}{3} + k π$

B. $x = \pm \frac{π}{3} + k 2 π$

C. $x = \pm \frac{π}{6} + k π$

D. $x = \pm \frac{π}{6} + k 2 π$

Xem đáp án

Đáp án B

Câu 37:

Cho a và b là hai số không âm. Đặt $X = 3^{\frac{a + b}{2}}, Y = \frac{3^{a} + 3^{b}}{2}$ . Khẳng định nào sau đây là đúng?

A. X > Y

B. X < Y

C. $X \geq Y$

D. $X \leq Y$

Xem đáp án

Đáp án D

Áp dụng bất đẳng thức Cosi ta có:

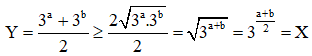
Câu 38:

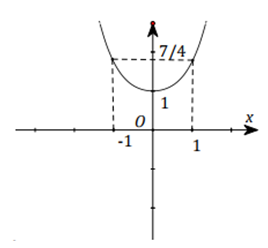
Một vật chuyển động trong một giờ với vận tốc v (km/h) phụ thuộc thời gian t(h) có đồ thị là một phần của đường parabol với đỉnh $I (\frac{1}{2}; 4)$ và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong khoảng thời gian 30 phút, kể từ khi bắt đầu chuyển động.

A. $s = 1, 33 (k m)$

B. $s = 1, 43 (k m)$

C. $s = 1, 53 (k m)$

D. $s = 1, 73 (k m)$

Xem đáp án

Đáp án A

Câu 39:

Cho dãy số $(u_{n})$ với $u_{n} = \frac{2^{n} - 5^{n}}{2^{n} + 5^{n}}, n \geq 1$ . Tính tổng $S = \frac{1}{u_{1} - 1} + \frac{1}{u_{2} - 1} + \frac{1}{u_{3} - 1} + ... + \frac{1}{u_{50} - 1}$

A. $S = \frac{2^{51} + {152.5}^{50}}{{6.5}^{50}}$

B. $S = \frac{2^{51} - {152.5}^{50}}{6}$

C. $S = \frac{2^{51} + {152.5}^{50}}{6}$

D. $S = \frac{2^{51} - {152.5}^{50}}{{6.5}^{50}}$

Xem đáp án

Đáp án D

Câu 40:

Tính $L = \underset{x \to 0}{l i m} \frac{\sqrt[n]{1 + a x} - 1}{x}, a \neq 0$ .

A. $L = \frac{a}{n}$

B. $L = \frac{n}{a}$

C. L = a.n

D. $L = \frac{1}{a . n}$

Xem đáp án

Đáp án A

$\begin{array}{l} L = \underset{x \to 0}{l i m} \frac{\sqrt[n]{1 + a x} - 1}{x} \\ = \underset{x \to 0}{l i m} \frac{(\sqrt[n]{(1 + a x)} - 1) (1 + \sqrt[n]{1 + a x} + \sqrt[n]{1 + a x} + ... + \sqrt[n]{1 + a x})}{x (1 + \sqrt[n]{(1 + a x)} + \sqrt[n]{{(1 + a x)}^{2}^{}} + ... + \sqrt[n]{{(1 + a x)}^{n - 1}})} \\ = \underset{x \to 0}{l i m} \frac{1 + ax - 1}{x (1 + \sqrt[n]{1 + a x} + \sqrt[n]{1 + a x} + ... + \sqrt[n]{1 + a x})} = \frac{a}{n} \end{array}$

Câu 41:

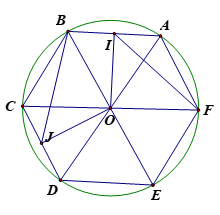
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O, gọi I là trung điểm của AB và J là trung điểm của CD. Hỏi ảnh của tam giác AIF qua phép quay tâm O, góc quay $120 °$ là tam giác nào dưới đây?

A. $Δ EJD$

B. $Δ F J E$

C. $Δ C J B$

D. $Δ OJD$

Xem đáp án

Đáp án C

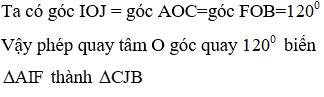
Câu 42:

Cho lăng trụ đứng $A B C A^{'} B^{'} C^{'}$ có đáy ABC là tam giác vuông tại A, $A B = a, A C B = 60 °, B' C$ tạo với mặt phẳng AA'CC' một góc $30 °$ . Tính thể tích V của khối lăng trụ $A B C A^{'} B^{'} C^{'}$ .

A. $V = a^{3} \sqrt{2}$

B. $V = a^{3} \sqrt{3}$

C. $V = \frac{a^{3} \sqrt{2}}{3}$

D. $V = \frac{a^{3} \sqrt{6}}{2}$

Xem đáp án

Đáp án C

Câu 43:

Cho hình chóp S.ABC có mặt bên SAB vuông góc với mặt phẳng đáy, tam giác SAB đều cạnh a, tam giác BAC vuông cân tại A. Tính khoảng cách h giữa hai đường thẳng AB và SC.

A. $h = \frac{a . \sqrt{3}}{\sqrt{7}}$

B. $h = \frac{a . \sqrt{3}}{7}$

C. $h = \frac{a . \sqrt{7}}{\sqrt{3}}$

D. $h = \frac{a . \sqrt{7}}{3}$

Xem đáp án

Đáp án A

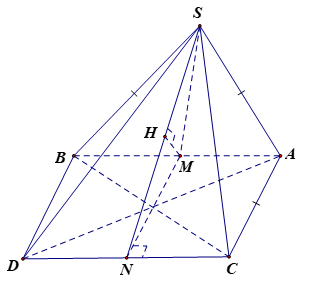
Dựng điểm D sao cho ABCD là hình vuông khi đó:

AB song song với (SDC)

=> khoảng cách giữa AB và SC

Bằng khoảng cách giữa AB và (SDC)

Gọi M,N lần lượt là trung điểm AB và DC ta có MN song song với AC nên MN vuông góc với AB. mà

SM vuông góc với AB nên AB vuông góc với (SMN). Do CD song song với AB nên CD vuông góc với (SMN) suy ra (SDC) vuông góc với (SMN)

Vì SN là giao tuyến của hai mặt phẳng trên => Kẻ MH vuông góc với SN thì MH là khoảng cách cần tìm.

Câu 44:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P) : 2 x - 2 y - z - 9 = 0$ và mặt cầu $(S) : {(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 100$ . Biết (P) cắt (S) theo giao tuyến là một đường tròn. Tìm tọa độ tâm của đường tròn giao tuyến.

A. (3;2;-1)

B. (-3;2;-1)

C. (3;-2;1)

D. (-3;2;1)

Xem đáp án

Đáp án C

Câu 45:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P) : x + y + z - 3 = 0$ và đường thẳng $Δ : \frac{x - 2}{1} = \frac{y + 1}{- 2} = \frac{z}{- 1}$ . Gọi I là giao điểm của $∆$ và (P). Tìm điểm M thuộc (P) có hoành độ dương sao cho MI vuông góc với $Δ v à M I = 4 \sqrt{14}$ .

A. $M = (5; 9; - 11)$

B. $M = (5; - 9; 11)$

C. $M = (- 5; 9; 11)$

D. $M = (5; 9; 11)$

Xem đáp án

Đáp án A

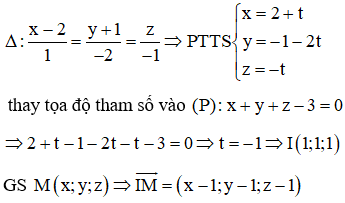
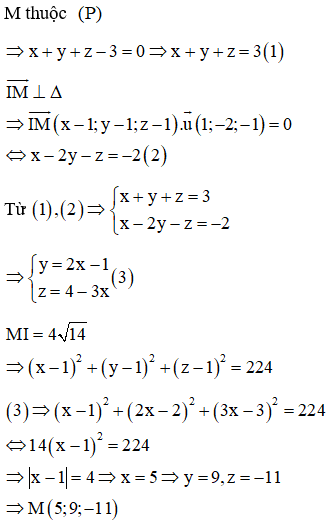
Câu 46:

Đội cờ đỏ của một trường phổ thông gồm 18 em, trong đó có 7 em thuộc khối 12, 6 em thuộc khối 11 và 5 em thuộc khối 10. Hỏi có bao nhiêu cách cử 8 em đi làm nhiệm vụ sao cho mỗi khối có ít nhất 1 em được chọn.

A. 44811 cách.

B. 51811 cách.

C. 44818 cách.

D. 41811 cách.

Xem đáp án

Đáp án D

Câu 47:

Tính tổng $S = \frac{1}{2} C_{19}^{0} - \frac{1}{3} C_{19}^{1} + \frac{1}{4} C_{19}^{2} - \frac{1}{5} C_{19}^{3} + ... + \frac{1}{20} C_{19}^{18} - \frac{1}{21} C_{19}^{19}$

A. $S = \frac{1}{420}$

B. $S = \frac{1}{240}$

C. $S = \frac{1}{440}$

D. $S = \frac{1}{244}$

Xem đáp án

Đáp án A

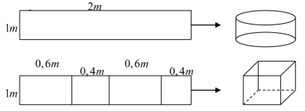
Câu 48:

Từ một tấm tôn có kích thước 1mx2m, người ta làm ra chiếc thùng đựng nước theo hai cách (xem hình minh họa dưới đây)

– Cách 1: làm ra thùng hình trụ có chiều cao 1m, bằng cách gò tấm tôn ban đầu thành mặt xung quanh của thùng.

- Cách 2: làm ra thùng hình hộp chữ nhật có chiều cao 1m, bằng cách chia tấm tôn ra thành 4 phần rồi gò thành các mặt bên của hình hộp chữ nhật. Kí hiệu $V_{1}$ là thể tích của thùng được gò theo cách 1 và $V_{2}$ là thể tích của thùng được gò theo cách 2. Tính tỷ số $\frac{V_{1}}{V_{2}}$ .

A. $\frac{V_{1}}{V_{2}} = \frac{1}{0, 24 π}$

B. $\frac{V_{1}}{V_{2}} = \frac{1}{0, 27 π}$

C. $\frac{V_{1}}{V_{2}} = \frac{1}{0, 7 π}$

D. $\frac{V_{1}}{V_{2}} = \frac{1}{0, 2 π}$

Xem đáp án

Đáp án A

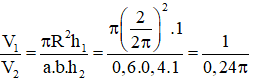
Câu 49:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (0; 0; 3), M (1; 2; 0)$ . Viết phương trình mặt phẳng (P) đi qua A và cắt Ox, Oy lần lượt tại B, C sao cho tam giác ABC có trọng tâm thuộc đường thẳng AM.

A. $(P) : 6 x + 3 y + 4 z - 12 = 0$

B. $(P) : 6 x + 3 y + 4 z + 12 = 0$

C. $(P) : 6 x + 3 y + 4 z - 2 = 0$

D. $(P) : 6 x + 3 y + 4 z + 2 = 0$

Xem đáp án

Đáp án A

Tam giác ABC có trọng tâm thuộc đường thẳng AM khi và chỉ khi trung điểm I của BC nằm trên đường thẳng AM.

Câu 50:

Khai triển đa thức ${(\frac{1}{3} + \frac{2}{3} x)}^{10}$ thành đa thức $a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + . . . + a_{9} x^{9} + a_{10} x^{10}$ $(a_{k} \in ℝ, k = 0, 1, 2, ..., 10)$

Tìm số lớn nhất trong các số $a_{0}, a_{1}, a_{2}, a_{3}, ..., a_{9}, a_{10}$

A. $a_{8}$

B. $a_{7}$

C. $a_{5}$

D. $a_{6}$

Xem đáp án

Đáp án B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải

Đề thi thử THPTQG môn Toán cực hay mới nhất có lời giải - đề 3

Danh sách câu hỏi

Bài thi liên quan