Hàm số liên tục
-
463 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
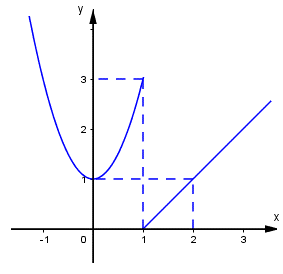
Hàm số có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Quan sát đồ thị ta thấy nên không tồn tại . Do đó hàm số gián đoạn tại điểm x = 1.
Đáp án cần chọn là: B
Câu 2:
Hàm số
 Xem đáp án
Xem đáp án
Hàm phân thức có txđ và liên tục trên các khoảng
Ta chỉ cần xét tính liên tục của tại các điểm
Ta có:
Hàm số liên tục tại
Hàm số liên tục tại
Vậy hàm số liên tục tại mọi điểm
Đáp án cần chọn là: C
Câu 3:
Cho hàm số . Để hàm số liên tục tại x = 8, giá trị của a là:
 Xem đáp án
Xem đáp án
Hàm số liên tục tại
Đáp án cần chọn là: A
Câu 5:
Hàm số
 Xem đáp án
Xem đáp án
Hàm số liên tục trên các khoảng nên ta chỉ xét tính liên tục của tại các điểm
⇒ hàm số liên tục tại
Không tồn tại ⇒ hàm số không liên tục tại x = 1.
Vậy hàm số liên tục tại mọi điểm trừ x = 1.
Đáp án cần chọn là: B
Câu 6:
Cho hàm số . Tìm a để hàm số liên tục tại x = 0.
 Xem đáp án
Xem đáp án
Ta có
Vậy để hàm số liên tục tại thì
Đáp án cần chọn là: B
Câu 7:
Cho phương trình . Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
TXĐ: D = R. Hàm số liên tục trên R.
Ta có: Phương trình (1) có ít nhất một nghiệm trong
⇒ Phương trình (1) có ít nhất hai nghiệm trong (−2;1)⇒ Đáp án A sai.
Ta có:
Phương trình (1) có ít nhất 1 nghiệm thuộc
⇒ Phương trình (1) có ít nhất hai nghiệm trong (−2;1)⇒ Đáp án A sai.
Ta có: Phương trình (1) có ít nhất một nghiệm trong Đáp án C sai.
Ta có: Phương trình (1) có ít nhất 1 nghiệm thuộc Đáp án D sai.
Đáp án cần chọn là: B
Câu 8:
Giá trị thực của tham số m để hàm số liên tục tại x = 2 bằng
 Xem đáp án
Xem đáp án
Bước 1:
Bước 2:
Đáp án cần chọn là: B
Câu 9:
Cho hàm số
Tìm tất cả các giá trị của tham số m để hàm số liên tục trên R.
 Xem đáp án
Xem đáp án
Ta có hàm số liên tục trên
Ta có:
Hàm số liên tục trên Hàm số liên tục trên và liên tục tại
⇔Hàm số xác định trên và liên tục tại
Thay m=5 vào (1) ta được
Vậy với m = 5 thì hàm số liên tục trên .
Đáp án cần chọn là: C
Câu 10:
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa aa và bb để hàm số liên tục tại x = 0.
 Xem đáp án
Xem đáp án
Bước 1:
Bước 2:
Để hàm số liên tục tại thì
Đáp án cần chọn là: B
Câu 11:
Cho hàm số f(x) liên tục trên đoạn sao cho . Có thể nói gì về số nghiệm của phương trình trên đoạn
 Xem đáp án
Xem đáp án
Ta có . Đặt Khi đó
Vậy phương trình có ít nhất một nghiệm thuộc khoảng (1;4) hay phương trình có ít nhất một nghiệm thuộc khoảng (1;4).
Đáp án cần chọn là: B
Câu 12:
Cho hàm số trong đó a,b là các tham số thực. Biết hàm số liên tục tại x = 3. Số nhỏ hơn trong hai số a và b là:
 Xem đáp án
Xem đáp án
Đặt
Ta có
Nếu a = 3 thì
Để hàm số liên tục tại x = 3
Nếu Hàm số không thể liên tục tại x = 3.
Vậy
Đáp án cần chọn là: B
Câu 13:
 Xem đáp án
Xem đáp án
Hàm số là hàm đa thức có tập xác định là nên liên tục trên . Do đó hàm số liên tục trên mỗi khoảng
Ta có
⇒(1) có ít nhất một nghiệm thuộc
⇒(1) có ít nhất một nghiệm thuộc (−1;0)
⇒(1) có ít nhất một nghiệm thuộc (0;2).
Như vậy phương trình (1) có ít nhất ba nghiệm thuộc khoảng (−2;2).
Tuy nhiên phương trình là phương trình bậc ba có nhiều nhất ba nghiệm.
Vậy phương trình có đúng 3 nghiệm trên .
Đáp án cần chọn là: D
