25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Chương 2: Đường thẳng - Mặt phẳng trong không gian cơ bản (phần 3) (có đáp án)

Câu 1:

Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mp (SAD) và mp (SBC) là đường thẳng song song với đường thẳng nào trong số các đường thẳng sau?

A. AC

B. BD

C. AD

D. SC

Xem đáp án

Đáp án C

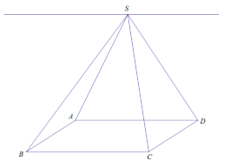
Xét (SAD) và (SBC) có:

S là điểm chung

AD // BC

$\Rightarrow$ giao tuyến của (SAD) và (SBC) là đường thẳng đi qua S và song song với AD

Câu 2:

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I,J lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Thiết diện tạo bởi mp(AIJ) với hình lăng trụ đã cho là:

A. Tam giác cân

B. Hình thang

C. Hình bình hành

D. Tam giác vuông

Xem đáp án

Đáp án C

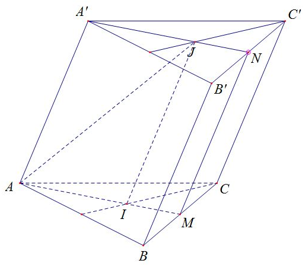
Xét tam giác A’B’C’:

Gọi N là trung điểm B’C’

J là trọng tâm A’B’C’

Xét tam giác ABC:

Gọi M là trung điểm BC

I là trọng tâm ABC

Từ (1), (2), ta có IJ // MN

Xét (AIJ) và (B’C’CB) có:

M là điểm chung

IJ // MN

$\Rightarrow$ giao tuyến của (AIJ) và (B’C’CB) là MN

$\Rightarrow$ thiết diện cần tìm là mặt phẳng (A’NMA)

Xét (A’NMA) có: A’A // MN và A’A = MN ( // = BB’)

A’NMA là hình hình hành

Câu 3:

Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:

A. GE//CD

B. GE và CD chéo nhau

C. GE cắt AD

D. GE cắt CD

Xem đáp án

Đáp án A

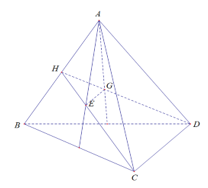
Gọi H là trung điểm của AB.

Xét tam giác HCD có:

$\Rightarrow$ EG // CD ( định lí ta- let)

Câu 4:

Cho hai hình vuông ABCD và ABEF không cùng nằm trên một mặt phẳng. Mệnh đề nào sau đây đúng?

A. AD//BE

B. (DAF)//(CBE)

C. DF//BC

D. (ABD)//(CFE)

Xem đáp án

Đáp án B

* Vì ABCD là hình vuông nên: AD // BC

Mà $B C \subset (C B E)$ nên AD// mp (CBE) (1)

* Vì ABEF là hình vuông nên: AF// BE

Mà $B E \subset (C B E)$ nên AF // mp ( CBE) (2)

* Vì hai đường thẳng AD; AF cắt nhau tại A và cùng nằm trong (DAF) (3)

từ (1);(2); (3) suy ra: (DAF)//(CBE)

Câu 5:

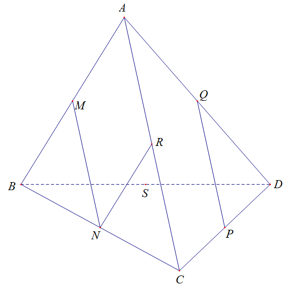
Cho tứ diện ABCD. Các điểm P,Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR=2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Tính tỉ số SA/SD là:

A. 2

B. 1/2

C. 1/3

D. 1

Xem đáp án

Đáp án A

Xét (BCD) có: RQ $\cap$ BD = $\{K\}$

$\Rightarrow$ K $\in$ (ABD)

Xét (ABD) có: PK $\cap$ AD = $\{S\}$

Gọi E là trung điểm BR

$\Rightarrow$ R là trung điểm đoạn EC

Mà Q là trung điểm CD

$\Rightarrow$ RQ là đường trung bình tam giác DEC

$\Rightarrow$ RQ // DE $\Rightarrow$ RK // DE

Xét tam giác BRK có: RK // DE và E là trung điểm BR

$\Rightarrow$ D là trung điểm BK

Xét tam giác ABK có: AD là đường trung tuyến cạnh BK

và KP là đường trung tuyến cạnh AB

PK $\cap$ AD = $\{S\}$

$\Rightarrow$ S là trọng tâm tam giác ABK

$\Rightarrow \frac{S A}{S D} = 2$

Câu 6:

Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Thiết diện của hình chóp khi cắt bởi mặt phẳng qua O, song song với AB và SC là hình gì?

A. Hình vuông

B. Hình bình hành

C. Hình chữ nhật

D. Hình thang

Xem đáp án

Đáp án D

Trong mặt phẳng (ABCD), kẻ đường thẳng d đi qua O và song song với AB

d cắt AD tại J

d cắt BC tại G

Trong mặt phẳng (SBC), kẻ đường thẳng Gx đi qua G và song song với SC; đường thẳng này cắt SB tại H

Trong mặt phẳng (SAB), kẻ đường thẳng y đi qua H và song song với AB

y cắt SA tại I

$\Rightarrow$ IHGJ là thiết diện cần tìm

Xét tứ giác IHGJ có: IH // JG ( // AB )

$\Rightarrow$ IHGJ là hình thang

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm F của cạnh AB, song song với BD và SA là hình gì?

A. Lục giác

B. Tam giác

C. Tứ giác

D. Ngũ giác

Xem đáp án

Đáp án D

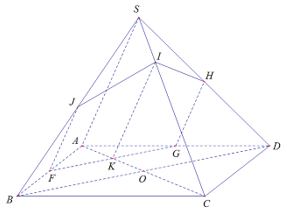
Trong (ABCD), kẻ đường thẳng d đi qua F và song song với BD

d cắt AD tại G

d cắt AC tại K $\Rightarrow F G \cap A C = \{K\}$

Trong (SAD), kẻ đường thẳng x đi qua G và song song với SA

x cắt SD tại H

Trong (SAB), kẻ đường thẳng y đi qua F và song song với SA

y cắt SB tại J

Trong (SAC), kẻ đường thẳng z đi qua K và song song với SA

z cắt AC tại I

$\Rightarrow$ FGHIK là thiết diện cần tìm

$\Rightarrow$ thiết diện là ngũ giác

Câu 8:

Cho hình bình hành ABCD. Gọi Bx,Cy,Dz lần lượt là các đường thẳng song song với nhau đi qua B,C,D và nằm về cùng một phía của mp(ABCD), đồng thời không nằm trong mp(ABCD). Một mặt phẳng đi qua Avà cắt Bx,Cy,Dz lần lượt tại B’,C’,D’ biết BB’=4, DD’=2. Khi đó CC’ bằng:

A. 3

B. 4

C. 5

D. 6

Xem đáp án

Đáp án D

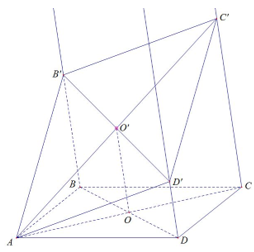
Trên Bx lấy điểm B’ sao cho BB’ = 4

Trên Dz lấy điểm D’ sao cho DD’ = 2

Gọi $(α)$ là mặt phẳng chứa tia Bx và Dz

Xét (AB’D’) và $(α)$ có:

B’ là điểm chung

AD’ // $(α)$

$\Rightarrow$ giao tuyến của $(α)$ và (AB’D’) là đường thẳng d đi qua B’ và song song với AD’

Trong mặt phẳng $(α)$ , ta có: d cắt Cz tại C’

Gọi $\{O\} = A C \cap B D, \{O'\} = A C' \cap B' D'$

Xét hình thang BB’D’D có: OO’ là đường trung bình

Xét tam giác ACC’ có: OO’ là đường trung bình

Câu 9:

Cho tứ diện ABCD và ba điểm E,F,G lần lượt nằm trên ba cạnh AB,BC,CD mà không trùng với các đỉnh (FG không song song với BD). Thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là:

A. Một tứ giác

B. Một tam giác

C. Một ngũ giác

D. Một đoạn thẳng

Xem đáp án

Đáp án A

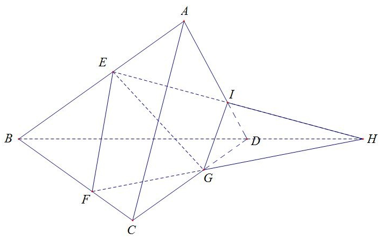
Trong mặt phẳng (BCD), $F G \cap B D = \{H\}$

H $\in$ BD $\Rightarrow$ H $\in$ (ABD)

Trong (ABD), $E H \cap A D = \{I\}$

$\Rightarrow$ tứ giác EFGI là thiết diện cần tìm

Câu 10:

Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:

A. Tam giác MNE

B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD

C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC

D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC

Xem đáp án

Đáp án C

Xét (MNE) và (BCD) có:

E là điểm chung

BC // MN $\Rightarrow$ BC // (MNE)

$\Rightarrow$ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC

d cắt BD tại H

$\Rightarrow$ MNEH là thiết diện cần tìm

Xét tứ giác MNEH có MN // EH ( // BC)

$\Rightarrow$ MNEH là hình thang

Câu 11:

Cho tứ diện ABCD. Gọi M,K lần lượt là trung điểm của BC và AC. N là điểm trên cạnh BD sao cho BN=2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau, mệnh đề nào đúng?

A. AF=3FD

B. AF=2FD

C. AF=FD

D. FD=2AF

Xem đáp án

Đáp án B

Xét (MNK) và (ABD) có:

N là điểm chung

AB // MK ( vì MK là đường trung bình của tam giác ABC) $\Rightarrow A B ⫽ (M N K)$

$\Rightarrow$ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua N và song song AB

d cắt AB tại điểm F cần tìm

Vì FN // AB ( cách dựng)

Câu 12:

Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC) là:

A. d cắt (ABC)

B. d $\subset$ (ABC)

C. d không song song (ABC)

D. d//(ABC)

Xem đáp án

Đáp án D

Xét (DMN) và (DBC) có:

D là điểm chung

BC // MN ( vì MN là đường trung bình của tam giác ABC) $\Rightarrow B C ⫽ (D M N)$

Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua D và song song với AB

$\Rightarrow$ d // mp(ABC)

Câu 13:

Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. Xét vị trí tương đối của đường thẳng MN và mp(BCD) là:

A. MN nằm trong (BCD)

B. MN không song song (BCD)

C. MN//(BCD)

D. MN cắt (BCD)

Xem đáp án

Đáp án C

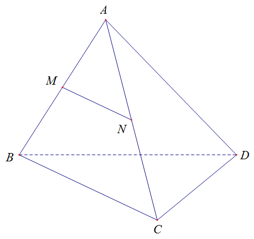
Xét tam giác ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.

Suy ra:MN // BC

Mà BC $\subset m p (B C D)$ nên MN // mp(BCD)

Câu 14:

Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mp qua M và song song với mp(SIC); biết AM=x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là:

A. 3x(1+ $\sqrt{3}$ )

B. 2x(1+ $\sqrt{3}$ )

C. x(1+ $\sqrt{3}$ )

D. Không tính được

Xem đáp án

Đáp án B

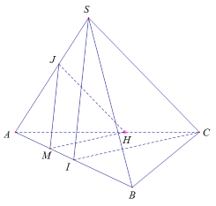
Trong (ABC), kẻ đường thẳng d đi qua M song song CI

d cắt AC tại H

Trong (SAB) kẻ đường thẳng x đi qua M và song song SI

X cắt SA tại J

$\Rightarrow$ (MHJ) là thiết diện cần tìm

Gọi tứ diện đều cạnh 2a $\Rightarrow$ AI = a

Ta có AM = x và $\frac{M J}{S I} = \frac{A M}{A I}$ (MJ // SI theo cách dựng)

$\frac{A M}{A I} = \frac{M H}{C I}$ (MH // CI theo cách dựng)

$\frac{J H}{S C} = \frac{A H}{A C} = \frac{A M}{A I}$

$\Rightarrow$ MJ = $\frac{x}{a} . \sqrt{3} a$ = $x \sqrt{3}$

MH = $\frac{x}{a} . \sqrt{3} a$ = $x \sqrt{3}$

JH = $\frac{x}{a} . 2 a$ = 2x

Chu vi thiết diện MHJ là: x $\sqrt{3}$ + x $\sqrt{3}$ + 2x = 2x ( $\sqrt{3}$ + 1 )

Câu 15:

Gọi G là trọng tâm của tứ diện ABCD. A’ là trọng tâm của tam giác BCD. Tính tỉ số GA/GA’ là:

A. 1/2

B. 2

C. 3

D. 1/3

Xem đáp án

Đáp án C

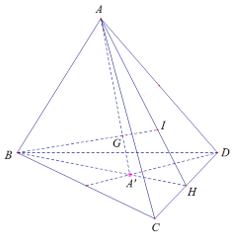
Gọi I là trọng tâm tam giác ACD

H là trung điểm CD

Nối BI cắt AA’, ta được trọng tâm G của tứ diện

Xét mặt phẳng (ABH)

Ta có: $\frac{I H}{A H} = \frac{A' H}{B H} = \frac{1}{3}$

( A’ và I lần lượt là trọng tâm các tam giác BCD và ACD)

$\Rightarrow$ A’I // AB

Ta lại có: $\frac{A' I}{A B} = \frac{G A'}{G A} = \frac{I H}{A H} = \frac{1}{3}$ ( áp dụng định lý ta lét)

$\Rightarrow$ GA = 3GA’

Câu 16:

Cho một hình hộp có độ dài ba cạnh cùng xuất phát từ một đỉnh lần lượt là 3,4,5. Tổng bình phương tất cả các đường chéo của hình hộp đó bằng:

A. 50

B. 60

C. 200

D. Không tính được

Xem đáp án

Đáp án C

(Dễ dàng chứng minh định lý: trong hình bình hành, tổng bình phương 2 đường chéo bằng tổng bình phương các cạnh bằng định lý hàm cos)

Ta có: $A C'^{2} = A A'^{2} + A' C'^{2}$

= $A A'^{2} + A' D'^{2} + A' B'^{2}$

= 50

Tương tự $B D'^{2} = A C'^{2} = D B'^{2} = C A'^{2} = 50$

Câu 17:

Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mặt phẳng (P). Gọi M là điểm nằm giữa S và A; N là điểm nằm giữa S và B; giao điểm của hai đường thẳng AC và BD là O; giao điểm của hai đường thẳng CM và SO là I; giao điểm của hai đường thẳng NI và SD là J. Tìm giao điểm của mp(CMN) với đường thẳng SO là:

A. A

B. J

C. I

D. B

Xem đáp án

Đáp án C

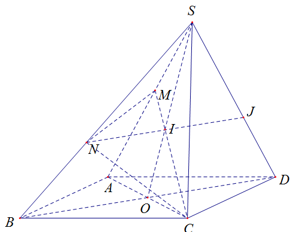
Trong (SAC) có SO cắt MC tại I

I $\in$ MC $\Rightarrow$ I $\in$ (MNC)

Mà I $\in$ SO

$\Rightarrow$ I là giao điểm của SO và (MNC)

Câu 18:

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’. Gọi d là giao tuyến của hai mặt phẳng (A’B’C’) và (A’BC). Thiết diện của hình lăng trụ khi cắt bởi mp(H,d) là hình gì?

A. Không xác định

B. Tam giác

C. Hình vuông

D. Hình bình hành

Xem đáp án

Đáp án B

Xét (A’B’C’) và (A’BC) có:

A’ là điểm chung

B’C’ // BC

giao tuyến của 2 mặt phẳng là đường thẳng d qua A’ song song với B’C’

$\Rightarrow$ d và B’C’ đồng phẳng

Mà d chứa A’

$\Rightarrow$ d thuộc mặt phẳng (A’B’C’)

Mà H $\in$ A’B’ $\Rightarrow$ H $\in$ (A’B’C’)

$\Rightarrow$ Mặt phẳng đi qua d và H, cắt tứ diện ABC. A’B’C’ là (A’B’C’)

Câu 19:

Cho hình bình hành ABCD. Gọi Ax, By,Cz,Dt lần lượt là các đường thẳng song song với nhau đi qua A,B,C,D và nằm về cùng một phía của mp(ABCD), đồng thời không nằm trong mp(ABCD). Một mặt phẳng (P) lần lượt cắt Ax,By,Cz,Dt lần lượt tại A’,B’,C’,D’ biết AA’=x,BB’=y, CC’=z. Khi đó DD’ bằng:

A. x+y-z

B. x-y-z

C. x-y+z

D. x+y+z

Xem đáp án

Đáp án C

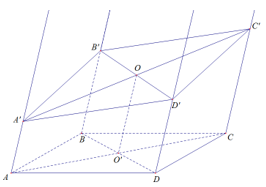
Trên Ax lấy điểm A’ sao cho AA’= x

Trên By lấy điểm B’ sao cho BB’ = y

Trên Cz lấy điểm C’ sao cho CC’ = z

Hai mp (AA'B'B) // ( DD'C'C) vì AA'// DD' và AB// DC

Mặt phẳng (P) cắt 2 mp song song (AA'B'B)và (DD'C'C) theo 2 giao tuyến là A'B'và C'D'

Suy ra: A'B' // C'D' ( định lí giao tuyến).

Gọi $\{O'\} = A C \cap B D, \{O\} = A' C' \cap B' D'$

Xét hình thang AA’C’C có: OO’ là đường trung bình

$\Rightarrow O O' = \frac{A A' + C C'}{2} = \frac{x + z}{2}$ (1)

Xét tam giác BDD’D có: OO’ là đường trung bình

$\Rightarrow O O' = \frac{D D' + B B'}{2} = \frac{D D' + y}{2}$ (2)

Từ (1) và (2) suy ra: x + z =DD' +y

Nên: DD’ = x + z – y

Câu 20:

Cho hình chóp S.ABCD. Gọi AB $\cap$ CD=J, AC $\cap$ BD=I, AD $\cap$ BC=K. Đẳng thức nào sai trong các đẳng thức sau?

A. (SAC) $\cap$ (SAD)=AB

B. (SAC) $\cap$ (SBD)=SI

C. (SAD) $\cap$ (SBC)=SK

D. (SAB) $\cap$ (SCD)=SJ

Xem đáp án

Đáp án A

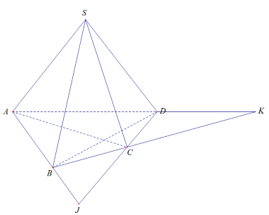
(SAC) $\cap$ (SAD)=SA

Câu 21:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. hai đường thẳng không cắt nhau và không song song thì chéo nhau

B. hai đường thẳng không song song thì chéo nhau

C. hai đường thẳng không có điểm chung thì chéo nhau

D. hai đường thẳng chéo nhau thì không có điểm chung

Xem đáp án

Đáp án D

Câu 22:

Cho 2 đường thẳng song song a và b. Trong các mệnh đề sau, mệnh đề nào sai ?

A. nếu mặt phẳng (P) cắt a thì cũng cắt b

B. Nếu mặt phẳng (P) song song với a thì cũng song song với b

C. Nếu mặt phẳng (P) song song với a thì mặt phẳng (P) hoặc song song với b hoặc mặt phẳng (P) chứa b

D. nếu mặt phẳng (P) chứa đường thẳng a thì cũng có thể chứa đường thẳng b

Xem đáp án

Đáp án B

Phương án B sai vì có thể xảy ra trường hợp : b nằm trên mp (P).

Câu 23:

Trong các mệnh đề sau, mệnh đề nào sai ?

A. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau

B. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì nó cắt mặt phẳng còn lại

C. Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó cắt mặt phẳng còn lại

D. Nếu một đường thẳng song song với một trong hai mặt phẳng song song thì nó song song với mặt phẳng còn lại

Xem đáp án

Đáp án D

Phương án D cần sửa lại thành:

Nếu một đường thẳng song song với một trong hai mặt phẳng song song thì hoặc nó song song hoặc nó nằm trong mặt phẳng còn lại

Câu 24:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. hình chiếu song song của 2 đường thẳng chéo nhau thì song song với nhau

B. hình chiếu song song của 2 đường thẳng cắt nhau có thể song song với nhau

C. hình chiếu song song của 2 đường thẳng chéo nhau có thể song song với nhau

D. các mệnh đề trên đều sai

Xem đáp án

Đáp án D

Câu 25:

Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Trong các mệnh đề sau, mệnh đề nào đúng?

A. hai đường thẳng RA và PQ cắt nhau

B. hai đường thẳng NR và PQ song song với nhau

C. hai đường thẳng MN và PQ song song với nhau

D. hai đường thẳng RA và MP chéo nhau

Xem đáp án

Đáp án C

Ta chứng minh phương án C đúng:
+ trong mp (ABC) có M và N lần lượt là trung điểm của AB; BC nên MN là đường trung bình của tam giác

Suy ra: MN // AC (1)
+ Trong mp( ACD) có P và Q lần lượt là trung điểm của CD và AD nên PQ là đường trung bình của tam giác

Suy ra: PQ// AC (2)

Từ (1) và (2) suy ra: MN// PQ

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song (có đáp án)

Trắc nghiệm Toán 11 Chương 2: Đường thẳng - Mặt phẳng trong không gian cơ bản (phần 3) (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương