Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 9)
-
6207 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
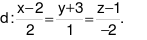 Vectơ nào dưới đây là một vectơ chỉ phương của d?
Vectơ nào dưới đây là một vectơ chỉ phương của d?Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Đường thẳng  có một VTCP là
có một VTCP là 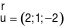 .
.
Câu 2:
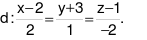 Vectơ nào dưới đây là một vectơ chỉ phương của d?
Vectơ nào dưới đây là một vectơ chỉ phương của d?Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Đường thẳng  có một VTCP là
có một VTCP là 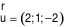 .
.
Câu 3:
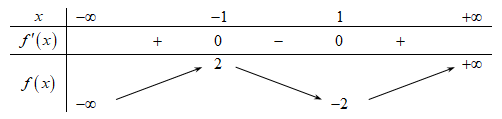
Giá trị cực tiểu của hàm số đã cho là
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Giá trị cực tiểu của hàm số 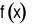 là
là 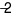 .
.
Câu 4:
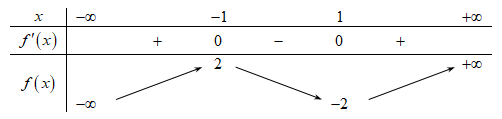
Giá trị cực tiểu của hàm số đã cho là
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Giá trị cực tiểu của hàm số 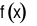 là
là 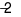 .
.
Câu 5:
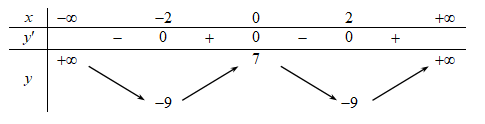
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Hàm số 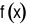 nghịch biến trên
nghịch biến trên  .
.
Câu 6:
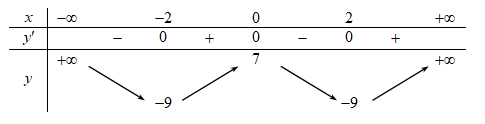
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Hàm số 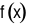 nghịch biến trên
nghịch biến trên  .
.
Câu 7:
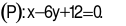 Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Mặt phẳng  có một VTPT là
có một VTPT là 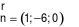 .
.
Câu 8:
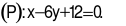 Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Mặt phẳng  có một VTPT là
có một VTPT là 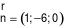 .
.
Câu 9:
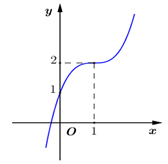
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có 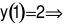 Loại B và D. Mà
Loại B và D. Mà 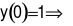 Chọn A.
Chọn A.
Câu 10:
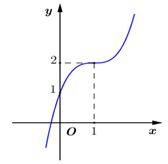
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có 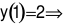 Loại B và D. Mà
Loại B và D. Mà 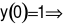 Chọn A.
Chọn A.
Câu 11:
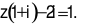
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Số phức  có phần thực phần
có phần thực phần  .
.
Câu 12:
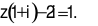
Lời giài:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Số phức  có phần thực phần
có phần thực phần  .
.
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án B
Ta loại ngay đáp án A và D.
Hàm trùng phương có 3 điểm cực trị .
Câu 16:
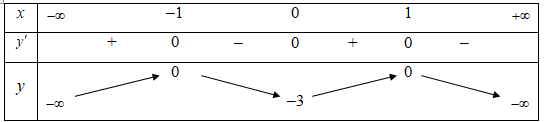
Số nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Đáp án D
Phương trình suy ra phương trình đã cho có 4 nghiệm phân biệt.Câu 17:
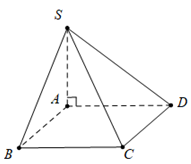
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Góc giữa (SBC) và mặt phẳng (ABCD) là góc
Lại có .Câu 18:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có: .
Mặt khác theo định lý Viet ta có .
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án A
Tâm . Cho ; .
Khi đó mặt cầu là .
Câu 22:
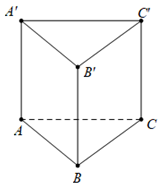
 Xem đáp án
Xem đáp án
Đáp án B
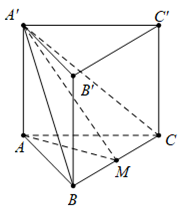
Dựng , lại có
Do đó
Mặt khác
Vậy .
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án B
Hàm số đạt cực trị tại x= 1.
Ta có
Phương trình có nghiệm đơn là 1 điểm cực trị của hàm sốCâu 25:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi R là bán kính của quả banh tenis hình cầu thì tổng thể tích của 4 quả banh là
Hình trụ có chiều cao bằng và bán kính đáy r = R
Thể tích của khối trụ là .
Suy ra .Câu 26:
Số nghiệm dương của phương trình là
 Xem đáp án
Xem đáp án
Đáp án B
Điều kiện
Khi đó PT
Vậy phương trình đã cho có 1 nghiệm dương
Câu 28:
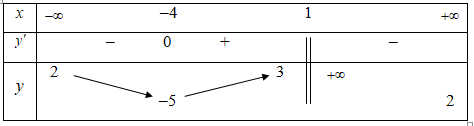
Số đường tiệm cận đứng và ngang của đồ thị hàm số đã cho là
 Xem đáp án
Xem đáp án
Đáp án B
Do nên đồ thị hàm số có 1 đường tiệm cận ngang y = 2.
Mặt khác nên đồ thị hàm số có 1 đường tiệm cận đứng x = 1.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:Câu 30:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có , là VTPT của mặt phẳng cần tìm => Phương trình mặt phẳng .
Câu 33:
Trong không gian Oxyz, phương trình đường thẳng qua cắt và vuông góc với đường thẳng d: là
 Xem đáp án
Xem đáp án
Đáp án D
Giả sử đường thẳng cần tìm cắt d tại
Ta có: do nên
Phương trình đường thẳng cần tìm là
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án B
Đặt ta có:
Vậy
Câu 35:
Tìm m để bất phương trình nghiệm đúng với mọi
 Xem đáp án
Xem đáp án
Đáp án D
Ta có: (với )
Xét hàm số với thì
Ta có bảng biến thiên
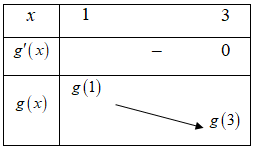
Do đó
Câu 36:
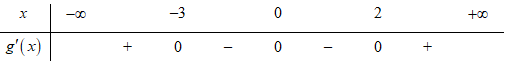
Hàm số nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án B
Chọn
Xét
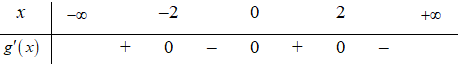
Suy ra g(x) nghịch biến trên khoảng (-2;0)
Câu 37:
Trong đợt tham quan thực tế, một Đoàn trường THPT cử 30 đoàn viên xuất sắc của 3 khối tham gia. Khối 12 có 6 nam và 4 nữ, khối 11 có 5 nam và 5 nữ, khối 10 có 4 nam và 6 nữ. Chọn mỗi khối 1 đoàn viên làm nhóm trưởng, tính xác suất để trong 3 em làm nhóm trưởng có cả nam và nữ.
 Xem đáp án
Xem đáp án
Đáp án D
Số phần tử của không gian mẫu là:
Gọi A là biến cố: 3 em làm nhóm trưởng có cả nam và nữ.
Khi đó là biến cố “3 học sinh được chọn chì có nam hoặc nữ”
Số kết quả thuận lợi cho biến cố là:
Xác suất của biến cố là
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án C
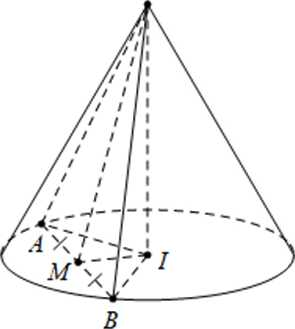
Dựng hình nón đỉnh O như hình vẽ ta có: .
Theo giả thiết ta có: ,
Gọi M là trung điểm AB
Dựng , đặt
Lại có:
Suy ra
Câu 39:
 Xem đáp án
Xem đáp án
Đáp án B
Phương trình đã cho tương đương
Xét hàm số với ta có .
Bảng biến thiên:
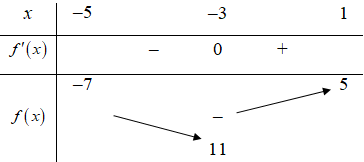
Dựa vào bảng biến thiên suy ra phương trình đã cho có 2 nghiệm phân biệt khi
Kết hợpCâu 40:
 Xem đáp án
Xem đáp án
Đáp án B
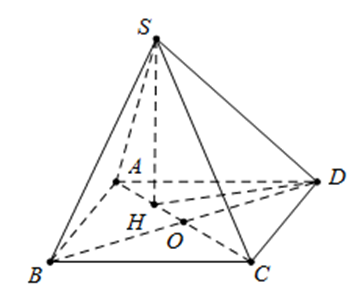
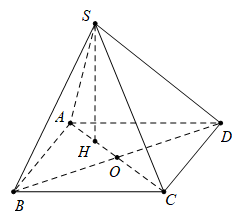
Ta có: ,
, .
Áp dụng công thức
Trong đó , ,
Suy raCâu 42:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi là điểm bất kì thuộc mặt cầu (S).
Ta có: và nên
Do nên suy ra thỏa mãn phương trình: .
Câu 43:
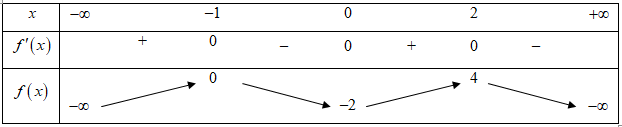
Có bao nhiêu giá trị nguyên của tham số m để phương trình có ít nhất 5 nghiệm thuộc khoảng ?
 Xem đáp án
Xem đáp án
Câu 44:
 Xem đáp án
Xem đáp án
Đáp án B
Đặt suy ra
Mà và .
Vậy w thuộc đường tròn tâm , bán kính .
Cách 2: Gọi ; biểu diễn số phức z1; z2
Ta có: tập hợp z là đường tròn tâm bán kính ;
Gọi H là trung điểm của (1)
Mặt khác tập hợp điểm H là đường tròn .
Giả sửCâu 45:
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
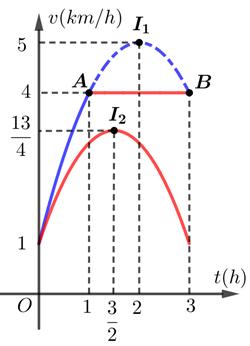
• Xét chiều di chuyển của vật M.
Gọi phương trình của parabol (P) là
Vì (P) có đỉnh I(2;5) và đi qua M(0;1) nên suy ra
Do đó, phương trình (P) là cùng chinh là phương trình vận tốc.
Suy ra quãng đường vật M đi trong 3 giờ là .
• Xét chiều di chuyển của vật N.
Gọi phương trình của parabol (P) là
Vì (P) có đỉnh và đi qua M(0;1) nên suy ra
Do đó, phương trình (P) là cũng chính là phương trình vận tốc.
Suy ra quãng đường vật N đi trong 3 giờ là .
Do hai vật đi ngược chiều nên khoảng cách của chúng là
Câu 46:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Do đó với
Ta có: (*)
Để hàm số có 3 điểm cực trị thì (*) có 3 nghiệm suy ra
Kết hợp và
Câu 47:
 Xem đáp án
Xem đáp án
Đáp án D
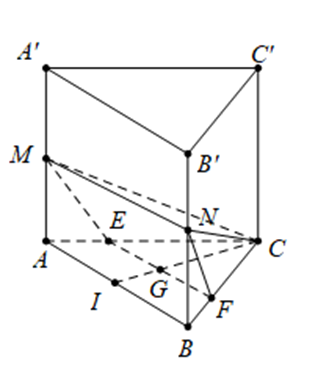
Do nên , qua G dựng đường thẳng song song với AB cắt BC, CA lần lượt tại F, E. Khi đó .
Áp dụng công thức nhanh ta có:
Do đó
Đặt ![]()
Khi đó
Do đó
Câu 48:
 Xem đáp án
Xem đáp án
Đáp án B
Xét (P): có tâm , bán kính R= 4.
Gọi O là hình chiếu của I trên mp (P). Ta có
Khi và chi khi với H là hình chiếu của I trên AB
là vectơ pháp tuyến của mp (P) mà H là trung điểm của AB.
là .
Câu 49:
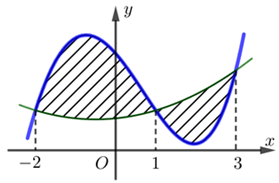
Cho hàm số f(x) có đạo hàm liên tục trên R và , . Biết hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số là?
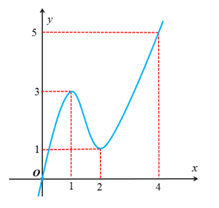
 Xem đáp án
Xem đáp án
Đáp án D
Nhắc lại: Số cực trị hàm số được tính bằng tổng số cực trị hàm số f(x) và giao điểm của hàm số f(x) với trục hoành.
Ta có
Xét (1)
Nếu thì phương trình (1) vô nghiệm
Nếu đặt thì (1) trở thành (2)
Vẽ đồ thị hai hàm số , trên cùng một hệ trục tọa độ.
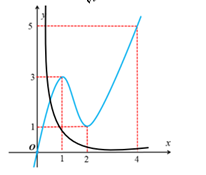
Quan sát hai đồ thị ta thấy
- Nếu thì hàm số f '(t) đồng biến, còn hàm số nghịch biến nên (2) có nghiệm duy nhất .
- Nếu thì nên (2) vô nghiệm.
Từ các nhận xét trên ta có bảng biến thiên
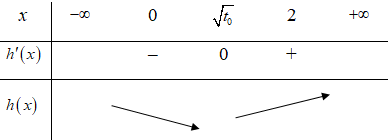
Ta có . Nên hàm số h(x) có một điểm cực tiểu và cắt trục hoành tại hai điểm phân biệt. Từ đó ta có có 3 cực trị.
