Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 10)
-
6208 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án C
Số phức liên hợp của số phức 1- 4i là 1+ 4i.
Câu 3:
Trong không gian Oxyz, cho mặt phẳng Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
 Xem đáp án
Xem đáp án
Đáp án A
Mặt phẳng có một VTPT
Câu 4:
Cho hàm số f(x) có bảng biến thiên như sau:
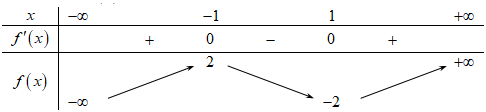
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án A
Hàm số f(x) đồng biến trên
Câu 7:
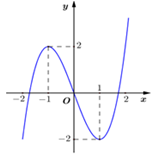
 Xem đáp án
Xem đáp án
Đáp án C
Ta có Loại B và D. Mà
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án D
Ta cóCâu 9:
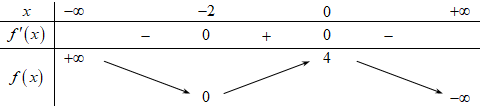
Hàm số đã cho đạt cực đại tại
 Xem đáp án
Xem đáp án
Đáp án B
Hàm số f(x) đạt cực đại tại x = 0Câu 10:
 Xem đáp án
Xem đáp án
Đáp án C
Theo quy tắc cộng, ta có 5 + 27 = 32 cách chọn một bạn làm lớp trưởngCâu 13:
 Xem đáp án
Xem đáp án
Đáp án A
Đường thẳng có một VTCP làCâu 14:
 Xem đáp án
Xem đáp án
Đáp án C
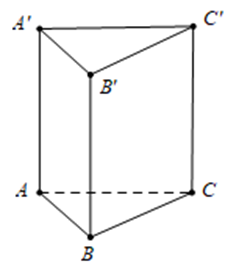
Ta có
Câu 16:
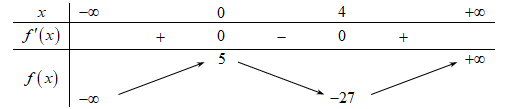
Phương trình có số nghiệm thực là
 Xem đáp án
Xem đáp án
Đáp án C
Đường thẳng cắt đồ thị hàm số tại đúng 3 điểm phân biệtCâu 18:
 Xem đáp án
Xem đáp án
Đáp án B
Ta cóCâu 20:
 Xem đáp án
Xem đáp án
Đáp án D
Ta có
Điểm biểu diễn số phức có tọa độ là
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án D
Mặt cầu (S) có tâm và bán kính
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án B
Trung điểm của đoạn thẳng AB làCâu 24:
Giá trị nhỏ nhất của hàm số trên đoạn bằng
 Xem đáp án
Xem đáp án
Đáp án A
Hàm số đã cho đã xác định và liên tục trên
Ta có
Tính
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án D
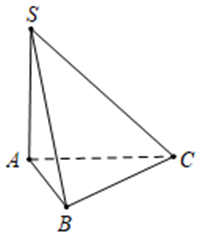
Ta có
Câu 27:
 Xem đáp án
Xem đáp án
Đáp án D
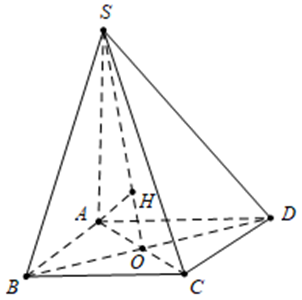
Gọi , kẻ
Cạnh
Câu 30:
 Xem đáp án
Xem đáp án
Đáp án C
Mặt phẳng (P) qua và nhận là một VTPT
Câu 31:
 Xem đáp án
Xem đáp án

Ta có
Cạnh
Câu 32:
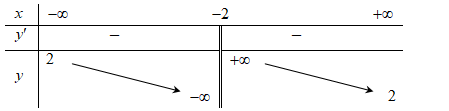
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
 Xem đáp án
Xem đáp án
Đáp án B
ĐTHS có tiệm cận đứng
Từ .Câu 33:
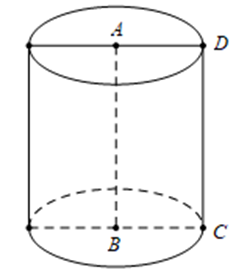
Trong không gian, cho hình chữ nhật ABCD với Tính thể tích V của khối trụ, nhận được khi quay hình chữ nhật ABCD xung quanh trục AB.
 Xem đáp án
Xem đáp án
Đáp án A
Câu 34:
 Xem đáp án
Xem đáp án
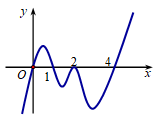
Đáp án C
Ta có
Qua thì f '(x) đổi dấu trên f(x) đạt cực trị tại
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án B
Điều kiện: Phương trình
Đặt ta được (1)
Phương trình đã cho có hai nghiệm thực phân biệt
có hai nghiệm thực dương phân biệt
Ta có thỏa mãn
Câu 36:
Trong không gian Oxyz, viết phương trình đường thẳng d là giao tuyến của mặt phẳng và
 Xem đáp án
Xem đáp án
Đáp án D
Cho qua
Cho qua
Đường thẳng d qua và nhận là một VTCP
Câu 37:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có
Để tiết kiệm nguyên liệu nhất thì phải nhỏ nhất.
Ta có
Dấu “=” xảy ra
Câu 38:
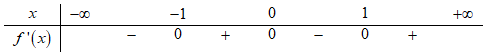
Hàm số y = f (2x - 1) đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có
Câu 39:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có Do
Ta có
Câu 40:
 Xem đáp án
Xem đáp án
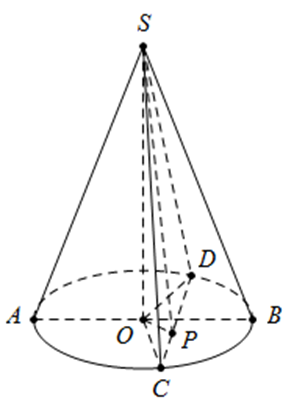
Thiết diện qua đỉnh của (N) là như hình vẽ.
Kẻ
Lại có
Từ
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án B
Có tất cả số tự nhiên có 3 chữ số.
Số cần tìm có dạng
+ TH1.
Nên có 7 số thỏa mãn.
+ TH2.
Nên có 2 số thỏa mãn.
Do đó có tất cả 9 số thỏa mãn. Vậy xác suất cần tìm là
Câu 42:
Cho các số thực a, b thỏa mãn .
Giá trị lớn nhất của biểu thức thuộc khoảng nào trong các khoảng sau đây?
 Xem đáp án
Xem đáp án
Đáp án A
ĐKXĐ:
+ Theo đề bài ra, ta có:
Xét hàm số sau:
Ta thấy: suy ra hàm số đồng biến trên
Do đó:
+ Khi đó:
Áp dụng định lí Bunhiacopski cho bộ hai số và ta có:
Do đó:
Suy ra: khi
Câu 43:
Cho hàm số y = f(x) liên tục, có đạo hàm trên R và có bảng biến thiên như hình vẽ
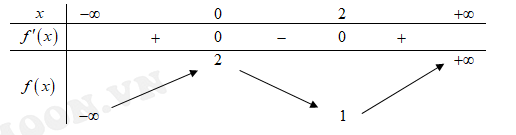
Hàm số đạt cực đại tại điểm nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 44:
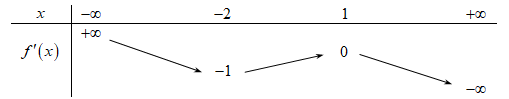
Bất phương trình có nghiệm với mọi khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án C
Xét hàm số
Với mọi thì
nghịch biến trên
Khi đó có nghiệm với mọi
Câu 45:
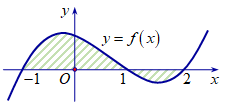
Cho hàm số có đồ thị , với m là tham số thực. Giả sử cắt trục Ox tại bốn điểm phân biệt như hình vẽ. Gọi là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm tất cả các giá trị thực của tham số m để
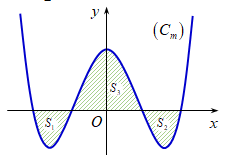
 Xem đáp án
Xem đáp án
Đáp án D
Ta có
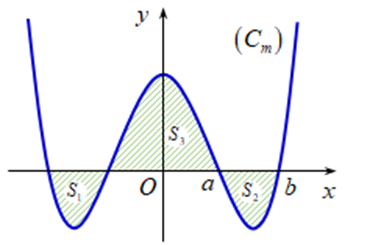
Mà
Câu 46:
 Xem đáp án
Xem đáp án
Đáp án A
Biến đổi
với
Ta có
Tính
Câu 47:
 Xem đáp án
Xem đáp án
Câu 48:
 Xem đáp án
Xem đáp án
Đáp án A
Ta có
Câu 49:
 Xem đáp án
Xem đáp án
Đáp án D
Giả sử
Ta có
Biến đổi
Giả sử
Tập hợp các điểm biểu diễn số phức là đường tròn có tâm và bán kính
Câu 50:
Trong không gian Oxyz, cho hai điểm nằm về hai phía của mặt phẳng (P). Khoảng cách từ điểm A đến mặt phẳng (P) bằng 3 và khoảng cách từ điểm B đến mặt phẳng (P) bằng 4. Mặt phẳng (P) đi qua điểm có tọa độ nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án D
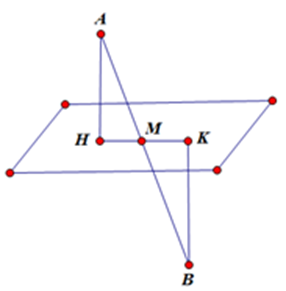
Kẻ với
Gọi ta có:
Mà
Do đó cần phải có H ở giữa A và B.
Khi đó
Mặt phẳng (P) qua H và nhận là một VTPT
