Giải SGK Toán 11 Hình học Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
Bài 4: Phép đối xứng tâm
-
2726 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chứng minh rằng M’ = ĐI(M) ⇔ M = ĐI(M')
Xem đáp án
M' = ĐI (M)nghĩa là phép biến hình này biến điểm I thành chính nó
hoặc biến mỗi điểm M khác I thành M' sao cho I là trung điểm
của đoạn thẳng MM’
- M ≡ I ⇒ M' = ĐI(M) ≡ M ≡ I ⇒ M = ĐI(M')
- M ≠ I ⇒ M' = ĐI(M) thì I là trung điểm của MM’
⇒ M' ≠ I và phép biến hình biến mỗi điểm M' thành M sao cho I là trung điểm của đoạn thẳng M'M
⇒ M = ĐI (M')
Câu 2:
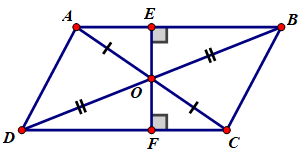
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo. Đường thẳng kẻ qua O vuông góc với AB, cắt AB ở E và cắt CD ở F. Hãy chỉ ra các cặp điểm trên hình vẽ đối xứng với nhau qua tâm O.
Xem đáp án
- Hình bình hành ABCD có O là giao điểm của hai đường chéo ⇒ O là trung điểm mỗi đường nên A và C đối xứng nhau qua tâm O
B và D đối xứng nhau qua tâm O
- Xét hai tam giác vuông AEO và CFO có:
OA = OC (do O là trung điểm AC)
= (hai góc đối đỉnh)
⇒ ΔAEO = ΔCFO (cạnh huyền – góc nhọn kề)
⇒ OE = OF (hai cạnh tương ứng)
Nên O là trung điểm EF
⇒ E và F đối xứng nhau qua tâm O
Câu 3:
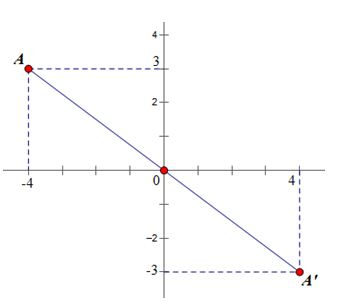
Trong mặt phẳng tọa độ Oxy cho điểm A(- 4; 3). Tìm ảnh của A qua phép đối xứng tâm O.
Xem đáp án
A'(a,b) là ảnh của A' qua phép đối xứng tâm O ⇒ a = 4 và b = -3
Câu 5:
Trong các chữ sau, chữ nào là hình có tâm đối xứng?
Xem đáp án
Các chữ có tâm đối xứng là: H, N, O, I