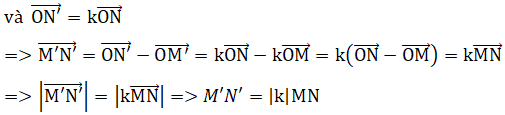5 câu hỏi trắc nghiệm thuộc Bài 8: Phép đồng dạng

Giải SGK Toán 11 Hình học Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

Câu 1:

Chứng minh nhận xét 2.

Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

Phép vị tự tâm O, tỉ số k biến điểm M, N thành 2 điểm M',N' sao cho OM→ = kOM→

Vậy phép vị tự tỉ số k là phép đồng dạng tỉ số |k|

Câu 2:

Chứng minh nhận xét 3.

Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk.

- Phép đồng dạng tỉ số k biến 2 điểm M, N thành 2 điểm M',N' sao cho M'N' = kMN

- Phép đồng dạng tỉ số b biến 2 điểm M',N' thành 2 điểm M'',N''sao cho M''N'' = pM'N'

⇒ M''N'' = pkMN

Vậy: Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk

Câu 3:

Chứng minh tính chất a.

Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

Phép đồng dạng tỉ số k biến 3 điểm A, B, C thẳng hàng thành 3 điểm A',B',C' sao cho:

A'B' = kAB, B'C' = kBC, A'C' = kAC

A, B, C thẳng hàng và B nằm giữa A, C ⇔ AB + BC = AC

Do đó kAB + kBC = kAC hay A'B' + B'C' = A'C'

⇒ A', B', C' thẳng hàng và B' nằm giữa A', C'

Câu 4:

Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’.

A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB

M’ = F(M) ⇒ A’M’ = kAM

M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’

Vậy M’ là trung điểm của A’B’

Câu 5:

Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau không?

Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau

Bắt đầu thi ngay