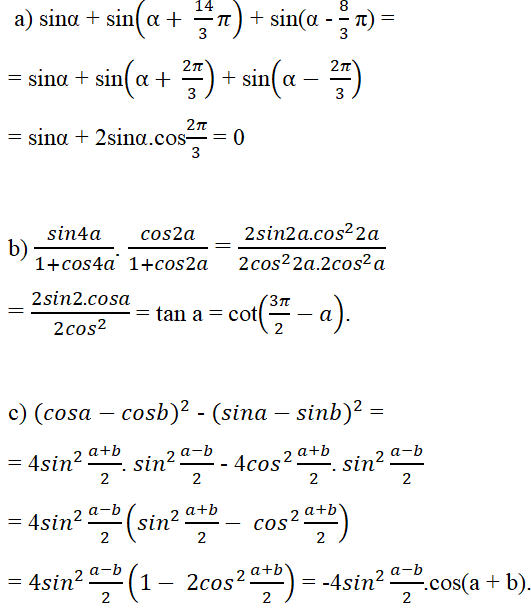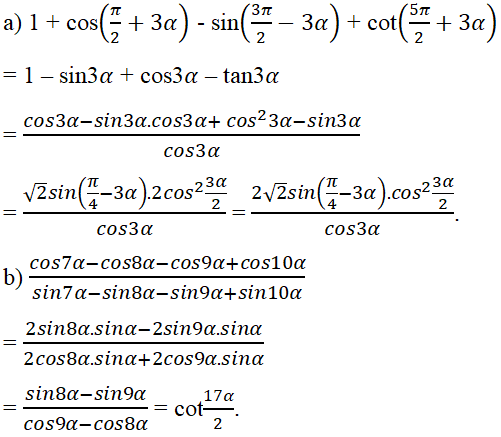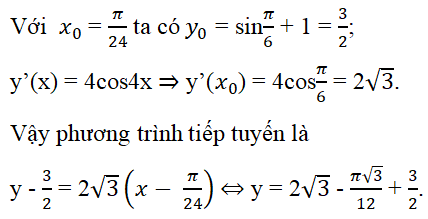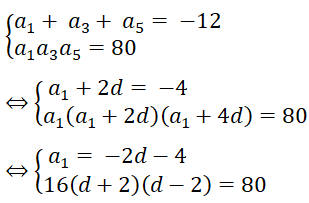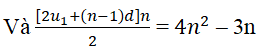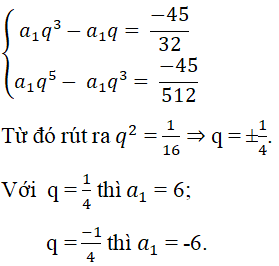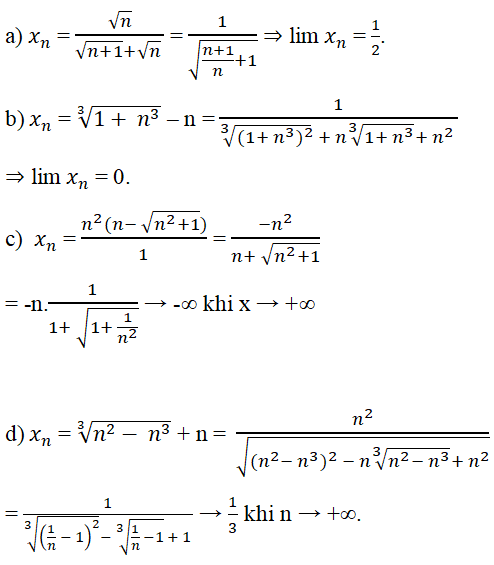22 câu hỏi trắc nghiệm thuộc Giải SBT Ôn tập cuối năm

Câu 1:

Chứng minh các hệ thức sau:

a) $sina + \sin (a + \frac{14}{3} π) + \sin (a - \frac{8}{3} π) = 0$ ;

b) $\frac{\sin 4 a}{1 + \cos 4 a} . \frac{\cos 2 a}{1 + \cos 2 a} = \cot (\frac{3}{2} π - a)$ ;

c) $\sin^{2} (45 ° + α) - \sin^{2} (30 ° - α) - \sin 15 ° \cos (15 ° + 2 α) = \sin 2 α$ ;

d) ${(cosa - cosb)}^{2} - {(sina - sinb)}^{2} = - 4 \sin^{2} \frac{a - b}{2} \cos (a + b)$ ;

Xem đáp án

d)

$\sin^{2} (45 ° + α) - \sin^{2} (30 ° - α) - \sin 15 ° . \cos (15 ° + 2 α) = [\sin (45 ° + α) + \sin (30 ° - α)] [\sin (45 ° + α) - \sin (30 ° - α)] - \sin 15 ° . \cos (15 ° + 2 α) = 2 \sin \frac{75 °}{2} . \cos (\frac{15 °}{2} + α) . 2 \cos \frac{75 °}{2} . \sin (\frac{15 °}{2} + α) - \sin 15 ° . \cos (15 ° + 2 α) = \sin 75 ° \sin (15 ° + 2 α) - \cos 75 ° \cos (15 ° + 2 α) = - \cos (90 ° + 2 α) = \cos (90 ° + 2 α) = \sin 2 α .$

Câu 2:

Biến đổi thành tích

$a) 1 + \cos (\frac{π}{2} + 3 α) - \sin (\frac{3}{2} π - 3 α) + \cot (\frac{5}{2} π + 3 α)$ ;

b) $\frac{\cos 7 α - \cos 8 α - \cos 9 α + \cos 10 α}{\sin 7 α - \sin 8 α - \sin 9 α + \sin 10 α}$ ;

c) $- \cos 5 acos 4 a - \cos 4 a \cos 3 a + 2 \cos^{2} 2 a cosa$ .

Xem đáp án

c) $- \cos 5 a . \cos 4 a - \cos 4 a . \cos 3 a + 2 \cos^{2} 2 a . cosa$

$= - \cos 4 a (\cos 5 a + \cos 3 a) + 2 \cos^{2} 2 a . cosa$

$= - 2 \cos 4 a . \cos 4 a . cosa + 2 \cos^{2} 2 a . cosa$

$= 2 cosa (\cos^{2} 2 a - \cos^{2} 4 a)$

$= 2 cosa (\cos 2 a + \cos 4 a) (\cos 2 a - \cos 4 a)$

$= 2 cosa . 2 \cos 3 a . cosa . 2 \sin 3 a . sina$

$= 2 cosa \sin 2 a \sin 6 a$ .

Câu 3:

Giả sử A, B, C là ba góc của tam giác ABC, chứng minh rằng:

a) $\frac{\sin C}{cosAcosB} = \tan A + \tan B$ ;

b) $\sin A + \sin B + \sin C = 4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}$ ;

c) $\frac{\sin A + \sin B + \sin C}{\sin A + \sin B - \sin C} = \cot \frac{A}{2} \cot \frac{B}{2} .$

Xem đáp án

a) HD: Thay $sinC = \sin (A + B)$ .

c) Chứng minh tương tự câu b) ta có

$sinA + sinB - sinC = 4 \sin (\frac{A}{2}) \sin (\frac{B}{2}) \cos (\frac{C}{2})$ (2)

Từ (1) và (2) suy ra điều phải chứng minh.

Câu 4:

Cho hàm số $y = \sin 4 x$

a) Chứng minh rằng $\sin 4 (x + \frac{kπ}{2}) = \sin 4 x$ với $k \in ℤ$

Từ đó vẽ đồ thị của hàm số

$y = \sin 4 x; (C_{1})$

$y = \sin 4 x + 1 . (C_{2})$

b) Xác định giá trị của m để phương trình: $\sin 4 x + 1 = m (1)$

- Có nghiệm

- Vô nghiệm

c) Viết phương trình tiếp tuyến của ( $C_{2}$ ) tại điểm có hoành độ $x_{0} = \frac{π}{24}$

Xem đáp án

a) Ta có $\sin 4 (x + \frac{kπ}{2}) = \sin (4 x + k 2 π) = \sin 4 x$ với $k \in ℤ$ . Từ đó suy ra hàm số $y = \sin 4 x$ là hàm số tuần hoàn với chu kì $\frac{π}{2}$ .

Vì hàm số $y = \sin 4 x$ là hàm số lẻ nên đồ thị của nó có tâm đối xứng là gốc tọa độ O.

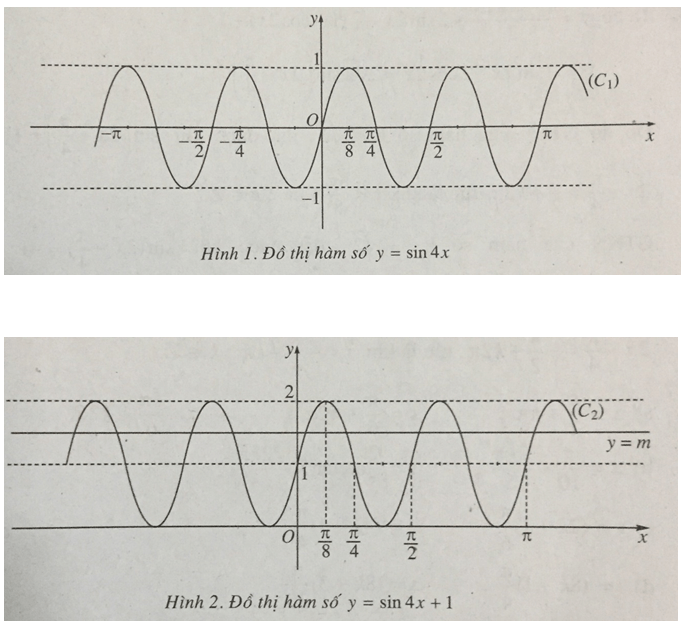
Các hàm số $y = \sin 4 x$ ( $C_{1}$ ) và $y = \sin 4 x + 1 (C_{2})$ có đồ thị như trên hình 1 và hình 2.

b) Vì $\sin 4 x + 1 = m \Leftrightarrow \sin 4 x = m - 1$

và $- 1 \leq \sin 4 x \leq 1$

nên $- 1 \leq m - 1 \leq 1$

$\Leftrightarrow 0 \leq m \leq 2$ .

Từ đó, phương trình (1) có nghiệm khi $0 \leq m \leq 2$ và vô nghiệm khi $m > 2$ hoặc $m < 0$ .

c) Phương trình tiếp tuyến của ( $C_{2}$ ) có dạng

$y - y_{o} = y ’ (x_{o}) (x - x_{o})$ .

Câu 5:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

$y = \sin^{2} x + 4 sinx . cosx - 3 \cos^{2} x + 1$

Xem đáp án

Ta có $y = \frac{(1 - \cos 2 x)}{2} + 2 \sin 2 x - \frac{3}{2 (1 + \cos 2 x)} + 1$

$= 2 \sin 2 x - 2 \cos 2 x = 2 \sqrt{2} \sin (2 x - \frac{π}{4})$ .

Do đó GTLN của hàm số là $2 \sqrt{2}$ , đạt được khi $\sin (2 x - \frac{π}{4}) = 1$ hay $2 x - \frac{π}{4} = \frac{π}{2} + k 2 π$ , tức là khi $x = \frac{3 π}{8} + kπ; k \in ℤ$ ;

GTNN của hàm số là $- 2 \sqrt{2}$ , đạt được khi $\sin (2 x - \frac{π}{4}) = - 1$ hay $2 x - \frac{π}{4} = \frac{- π}{2} + k 2 π$ , tức là khi $x = \frac{- π}{8} + kπ; k \in ℤ$ .

Câu 6:

Giải các phương trình

a) $\sin 2 x = \cos^{4} \frac{x}{4} - \sin^{4} \frac{x}{2}$ ;

b) $3 \sin 5 x - 2 \cos 5 x = 3$ ;

c) $\cos (\frac{π}{2} + 5 x) + \sin x = 2 \cos 3 x;$

d) $\sin 2 z + \cos 2 z = \sqrt{2} \sin 3 z$ .

Xem đáp án

a) $x = \frac{π}{2} + kπ$ ; $x = \frac{π}{6} + k 2 π; x = \frac{5 π}{6} + k 2 π$

b) $x = \frac{π}{10} + k \frac{2 π}{5}; x = \frac{2}{5} \arctan 5 + \frac{k 2 π}{5} .$ .

c) $x = (2 k + 1) \frac{π}{6}; x = (4 k - 1) \frac{π}{4}$ .

d) $x = (8 k + 1) \frac{π}{4}; x = (8 k + 3) \frac{π}{20}$ .

Câu 7:

Giải các phương trình

a) $\cos^{2} x + \cos^{2} 2 x - \cos^{2} 3 x - \cos^{2} 4 x = 0$ ;

b) $\cos 4 x \cos (π + 2 x) - \sin 2 x \cos (\frac{π}{2} - 4 x) = \frac{\sqrt{2}}{2} \sin 4 x;$

c) $\tan (120 ° + 3 x) - \tan (140 ° - x) = 2 \sin (80 ° + 2 x);$

d) $\tan^{2} \frac{x}{2} + \sin^{2} \frac{x}{2} \tan \frac{x}{2} + \cos^{2} \frac{x}{2} . \cot \frac{x}{2} + \cot^{2} \frac{x}{2} + sinx = 4$ ;

e) $\frac{\sin 2 t + 2 \cos^{2} t - 1}{cost - \cos 3 t + \sin 3 t - sint} = cost .$

Xem đáp án

a) $x = \frac{kπ}{2}; x = \frac{kπ}{5}$ .

b) $x = (2 k + 1) \frac{π}{4}; x = (- 1) (k + 1) \frac{π}{8} + \frac{kπ}{2}$ .

c) $x = - 40 ° + k 60 °$ .

d) $x = (4 k + 1) \frac{π}{2}; x = (- 1) (k + 1) \arcsin \frac{2}{3} + kπ$ .

e) $t = (4 k + 1) \frac{π}{4}$ .

Câu 8:

Có bao nhiêu số tự nhiên gồm tám chữ số, trong đó có đúng hai chữ số 2?

Xem đáp án

Giả sử chữ số 2 đứng đầu. Khi đó, chữ số 2 kia sẽ được xếp vào một trong 7 chỗ còn lại. Có 7 cách. Khi đã sắp xếp xong hai chữ số 2, còn 6 chỗ, ta xếp 9 chữ số khác 2 vào 6 chỗ đó. Ta có $9^{6}$ cách. Theo quy tắc nhân, có $7 . 9^{6}$ số gồm 8 chữ số mà chữ số hai đứng đầu.

• Chữ số 2 không đứng đầu. Khi đó, trong 8 chữ số khác 0 và khác 2, ta chọn một chữ số để xếp vào vị trí đầu. Có 8 cách.

Chọn 2 chỗ trong 7 chỗ để xếp hai chữ số 2. Có $C_{7}^{2}$ cách.

Xếp 9 chữ số (khác 2) vào năm vị trí còn lại, có $9^{5}$ cách.

Theo quy tắc nhân, có $8 . C_{7}^{2} . 95$ số mà chữ số 2 không đứng đầu.

Theo quy tắc cộng , số các số có 8 chữ số mà có đúng hai chữ số 2 là

$7 . 9^{6} + 8 . C_{7}^{2} . 95 = 13640319$

Câu 9:

Một tổ có 10 học sinh trong đó có An, Bình, Chi, Dung và Hương. Có bao nhiêu các xếp 10 bạn đó vào 10 ghế sắp thành hàng ngang sao cho An, Bình ngồi cạnh nhau và Chi, Dung, Hương cũng ngồi cạnh nhau?

Xem đáp án

Đầu tiên ta chỉ dung 7 ghế và xếp An, Chi và 5 bạn không thuộc nhóm An, Chi vào 7 ghế. Ta có 7! cách xếp. Sau đó xếp Bình ngồi cạnh An. Có 2! cách. Cuối cùng xếp Chi, Hương ngồi cùng nhóm với Dung. Ta có 3! cách. Theo quy tắc nhân, có 7! 2! 3! = 60480 cách.

Câu 10:

Học sinh A thiết kế bảng điều khiển điện tử mở cửa phòng học của lớp mình. Bảng gồm 10 nút, mỗi nút được ghi một số từ 0 đến 9 và không có hai nút nào được ghi cùng một số. Để mở cửa cần nhấn liên tiếp 3 nút khác nhau sau cho 3 số trên nút đó theo thứ tự đã nhấn tạo thành một dãy số tăng và có tổng bằng 10. Học sinh B không biết quy tắc mở cửa trên, đã nhấn ngẫu nhiên liên tiếp 3 nút khác nhau trên bảng điều khiển. Tính xác xuất để B mở được cửa phòng học đó. (Đề thi THPT Quốc gia 2016)

Xem đáp án

Số cách chọn 3 nút để ấn là $A_{10}^{3}$ = 720.

Số trường hợp đạt yêu cầu là: (0, 1, 9); (0, 2, 8); (0, 3, 7); (0, 4, 6); (1, 2, 7); (1, 3, 6);

(1, 4, 5) ; (2, 3, 5).

Xác xuất để B mở được cửa là $\frac{8}{720} = \frac{1}{90}$ .

Câu 11:

Tìm cấp số cộng $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ , biết rằng

$a_{1} + a_{3} + a_{5} = - 12$ và $a_{1} a_{3} a_{5} = 80$

Xem đáp án

Kí hiệu công sai là d, ta có

Giải ra ta được d = ± 3.

Các cấp số cộng phải tìm là

2, -1, -4, -7, …

Và -10, -7, -4, -1,….

Câu 12:

Viết ba số hạng đầu của một cấp số cộng, biết rằng tổng n số hạng đầu tiên của cấp số này là: $S_{n} = 4 n^{2} - 3 n$

Xem đáp án

Ta có $S_{1} = u_{1} = 4 . 1^{2} - 3.1 = 1$

⇒ $[2 + (n - 1) d] = 2 (4 n - 3) \Rightarrow d = 8$ .

Từ đó $u_{1} = 1, u_{2} = 9, u_{3} = 17$ .

Câu 13:

Tìm số hạng thứ nhất $a_{1}$ và công bội q của một cấp số nhân ( $a_{n}$ ), biết rằng

$a_{4} - a_{2} = - 1 \frac{13}{32}$ và $a_{6} - a_{4} = \frac{- 45}{512}$

Xem đáp án

Ta có hệ phương trình

Câu 14:

Hãy tính giới hạn $\lim_{x \to + \infty} x_{n}$ :

a) $x_{n} = \frac{\sqrt{n}}{\sqrt{n + 1} + \sqrt{n}}$ ;

b) $x_{n} = \sqrt[3]{1 + n^{3}} - n$ ;

c) $x_{n} = n^{2} (n - \sqrt{n^{2} + 1})$ ;

d) $x_{n} = \sqrt[3]{n^{2} - n^{3}} + n$ .

Xem đáp án

Câu 15:

Tinh giới hạn của hàm số $x \to \infty$

a) $x_{n} = \frac{\sqrt{n^{2} + 1} + \sqrt{n}}{\sqrt[3]{n^{3} + n} - n}$ ;

b) $x_{n} = (n - \frac{1}{n}) (\frac{1 - 4 n}{2 n^{2}})$ .

Xem đáp án

Câu 16:

Xét tính bị chặn của các dãy số với số hạng tổng quát sau:

a) $x_{n} = \frac{5 n^{2}}{n^{2} + 3}$ ;

b) $y_{n} = {(- 1)}^{n} \frac{2 n}{n + 1} \sin n$ ;

$z_{n} = ncosnπ$ .

Xem đáp án

Câu 17:

Tính các giới hạn sau

a) $\lim_{x \to 1} \frac{4 x^{5} + 9 x + 7}{3 x^{6} + x^{3} + 1}$ ; b) $\lim_{x \to 2} \frac{x^{3} + 3 x^{2} - 9 x - 2}{x^{3} - x - 6}$ ;

c) $\lim_{x \to - 1} \frac{x + 1}{\sqrt{6 x^{2} + 3} + 3 x}$ ; d) $\lim_{x \to 0} \frac{\sqrt{9 + 5 x + 4 x^{2}} - 3}{x}$ ;

e) $\lim_{x \to 2} \frac{\sqrt[3]{10 - x} - 2}{x - 2}$ ; f) $\lim_{x \to 1} \frac{\sqrt{x + 8} - \sqrt{8 x + 1}}{\sqrt{5 - x} - \sqrt{7 x - 3}}$ .

Xem đáp án

a) 4. c) 1.

b) 5/11. d) 5/6.

e) (-1)/12. f) 7/12.

Câu 18:

Tính các giới hạn

a) $\lim_{x \to + \infty} (\frac{x^{3}}{3 x^{2} - 4} - \frac{x^{2}}{3 x + 2})$ ;

b) $\lim_{x \to + \infty} (\sqrt{9 x^{2} + 1} - 3 x)$ ;

c) $\lim_{x \to - \infty} (\sqrt{2 x^{2} - 3} - 5 x)$ ;

d) $\lim_{x \to + \infty} \frac{\sqrt{2 x^{2} + 3}}{4 x + 2}$ ;

e) $\lim_{x \to - \infty} \frac{\sqrt{2 x^{2} + 3}}{4 x + 2}$

Xem đáp án

Câu 19:

Tính các giới hạn

a) $\lim_{x \to a} \frac{sinx - sina}{x - a}$ ;

b) $\lim_{x \to 1} (1 - x) \tan \frac{πx}{2}$ ;

c) $\lim_{x \to \frac{π}{3}} \frac{2 \sin^{2} x - sinx - 1}{2 \sin^{2} x - 3 sinx + 1}$ ;

d) $\lim_{x \to 0} \frac{tanx - sinx}{\sin^{3} x}$ .

Xem đáp án

Câu 20:

Tính đạo hàm của các hàm số sau:

a) $y = \frac{1 + x - x^{2}}{1 - x + x^{2}}$ ;

b) $y = \frac{(2 - x^{2}) (3 - x^{3})}{{(1 - x)}^{2}}$ ;

c) $y = \cos 2 x - 2 sinx$ ;

d) $y = \frac{cosx}{2 \sin^{2} x}$ ;

e) $y = \cos^{2} \frac{x}{3} \tan \frac{x}{2}$ ;

f) $y = \sqrt{\sin \sqrt{(2 x - \frac{π}{6})}}$ ;

g) $y = \cos \frac{x}{x + 1}$ ;

h) $y = \frac{x^{2} - 1}{\sin 3 x}$ ;

i) $y = 3 \sin^{2} x . cosx + \cos^{2} x$ ;

k) $y = \sqrt{7 - 4 x} . \cot 3 x$ .

Xem đáp án

Câu 21:

Cho hàm số

$f (x) = \{\begin{cases} x^{2} \sin \frac{1}{x}, nêu x \neq 0 \\ A, nêu x = 0 \end{cases}$

Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?

Xem đáp án

A = 0. Khi đó f(x) có đạo hàm tại x = 0.

Câu 22:

Cho hàm số $y = - x^{4} - x^{2} + 6$ (C)

a) Tính y', y''.

b) Tính y'''(-1), y'''(2)

c) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y = \frac{x}{6} - 1$

(Đề thi Đại học khối D năm 2010)

Xem đáp án

a) $y ’ = - 4 x^{3} - 2 x, y ’ ’ = - 12 x^{2} - 2$ .

b) $y ’ ’ ’ (x) = - 24, y ’ ’ ’ (- 1) = 24, y ’ ’ ’ (2) = - 48$ .

c) Phương trình tiếp tuyến tại điểm ( $x_{o}; y_{o}$ ) có dạng: $y - y_{o} = y ’ (x_{o}), (x - x_{o})$ .

Vì tiếp tuyến vuông góc với đường thẳng $y = \frac{1}{6} x - 1 nên y ’ (x_{o}) = - 6$ . Ta có

$- 4 x_{o}^{3} - 2 x_{o} = - 6 \Leftrightarrow 2 x_{o}^{3} + x_{o} - 3 = 0 \Leftrightarrow (x_{o} - 1) (2 x_{o}^{2} + 2 x_{o} + 3) = 0$

⇒ $x_{o} = 1; y_{o} = 4$ .

Phương trình tiếp tuyến phải tìm là $y - 4 = - 6 (x - 1) \Leftrightarrow y = - 6 x + 10$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 11 Chương 5: Đạo hàm

Giải SBT Ôn tập cuối năm

Danh sách câu hỏi

Bài thi liên quan