Giải VBT Toán 7 Cánh diều Bài 6. Trường hợp thứ ba của tam giác: góc - cạnh - góc có đáp án
Giải VBT Toán 7 Cánh diều Bài 6. Trường hợp thứ ba của tam giác: góc - cạnh - góc có đáp án
-
189 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
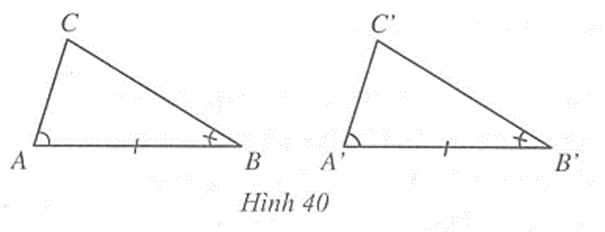
- Nếu một cạnh và hai góc kề nhau của tam giác này bằng ………. và ………. của tam giác kia thì hai tam giác đó bằng nhau.
Nếu \(\widehat A\) = \(\widehat {A'}\), AB = A’B’, \(\widehat B\) = \(\widehat {B'}\) thì ∆ABC = ∆A’B’C’ (g.c.g) (Hình 40).
Xem đáp án
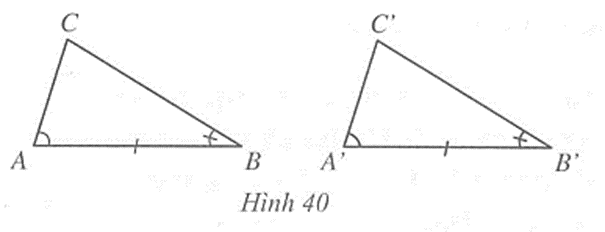
- Nếu một cạnh và hai góc kề nhau của tam giác này bằng một cạnh và hai góc kề nhau của tam giác kia thì hai tam giác đó bằng nhau.
Nếu \(\widehat A\) = \(\widehat {A'}\), AB = A’B’, \(\widehat B\) = \(\widehat {B'}\) thì ∆ABC = ∆A’B’C’ (g.c.g) (Hình 40).
Câu 2:
Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng …………. và ………………kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng ………. và ………… của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Nhận xét
+ Nếu một điểm nằm trên tia phân giác của một góc thì …….. hai cạnh đó
+ Nếu một điểm nằm trong một góc và ………..……. hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Xem đáp án
- Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Nhận xét
+ Nếu một điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
+ Nếu một điểm nằm trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Câu 3:
Cho hai tam giác ABC và A’B’C’ thoả mãn: BC = B’C’ = 3 cm, \(\widehat B\) = \(\widehat {B'}\) = 60o, \(\widehat C\) = 50o, \(\widehat {A'}\) = 70o. Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Xem đáp án
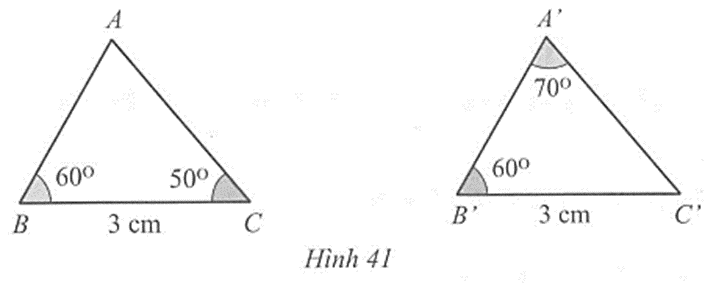
Xét tam giác A’B’C’, ta có: \(\widehat {A'}\) + \(\widehat {B'}\) + \(\widehat {C'}\) = 180o, (tổng ba góc của một tam giác)
Suy ra cm, \(\widehat {C'}\) = 180o – (\(\widehat {A'}\) + \(\widehat {B'}\)) = 180o – ( 70o + 60o) = 50o.
Xét hai tam giác ABC và A’B’C’ ta có:
BC = B’C’ = 3 cm, \(\widehat B\) = \(\widehat {B'}\) = 60o, \(\widehat C\) = \(\widehat {C'}\) = 50o,
Suy ra ∆ABC = ∆A’B’C’ (g.c.g).
Câu 4:
Có ba trạm quan sát A, B, C, trong đó trạm quan sát C ở giữa hồ. Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được khoảng cách trên nên người ta làm như sau (Hình 42):
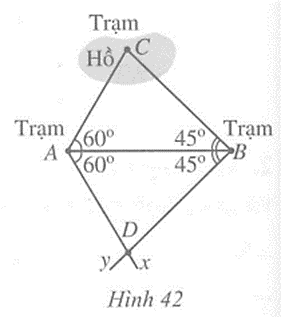
- Đo góc BAC được 60o, đo góc ABC được 45o.
- Kẻ tia Ax sao cho \(\widehat {{\rm{BAx}}}\) = 60o, kẻ tia By sao cho \(\widehat {ABy}\) = 45o, xác định giao điểm D của hai tia đó.
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Em hãy giải thích cách làm đó.
Xem đáp án
Xét hai tam giác ABC và ABD, ta có:
\(\widehat {CAB}\) = \(\widehat {DAB}\)= 60o, \(\widehat {CBA}\) = \(\widehat {DBA}\)= 45o, AB là cạnh chung
Suy ra ∆ABC = ∆ABD (g.c.g).
Do đó AC = AD, BC = BD (hai cạnh tương ứng)
Câu 5:
Cho hai tam giác ABC và A’B’C’ thoả mãn: AB = A’B’, \(\widehat A\) = \(\widehat {A'}\), \(\widehat C\) = \(\widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Xem đáp án
Xét hai tam giác ABC và A’B’C’, ta có: , \(\widehat A\) + \(\widehat B\) + \(\widehat C\) = \(\widehat {A'}\) + \(\widehat {B'}\) + \(\widehat {C'}\) = 180o (tổng ba góc của một tam giác)
Mà \(\widehat A\) = \(\widehat {A'}\), \(\widehat C\) = \(\widehat {C'}\)(giả thiết) nên \(\widehat B\) = \(\widehat {B'}\)
Xét hai tam giác ABC và A’B’C’, ta có:
AB = A’B’ (giả thiết), \(\widehat A\) = \(\widehat {A'}\) và \(\widehat B\) = \(\widehat {B'}\)
Suy ra: ∆ABC = ∆A’B’C’ (g.c.g).
Câu 6:
Cho Hình 43 có AM = BN, \(\widehat A\) = \(\widehat B\). Chứng minh OA = OB và OM = ON.
Xem đáp án
Xét hai tam giác OAM và OBN, ta có:
\(\widehat A\) + \(\widehat M\) + \(\widehat {AOM}\) = \(\widehat B\) + \[\widehat N\] + \(\widehat {BON}\) = 180o (tổng ba góc của một tam giác)
Mà \(\widehat A\) = \(\widehat B\), \(\widehat {AOM}\) = \(\widehat {BON}\) (hai góc đối đỉnh) nên \(\widehat M\) = \(\widehat N\)
Xét hai tam giác OAM và OBN, ta có:
AM = BN (giả thiết), \(\widehat A\) = \(\widehat B\) và \(\widehat M\) = \(\widehat N\)
Suy ra ∆OAM = ∆OBN (g.c.g)
Do đó OA = OB, OM = ON (hai cạnh tương ứng).
Câu 7:
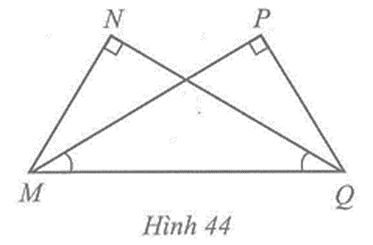
Cho Hình 44 có \(\widehat N\) = \(\widehat P\) = 90o, \(\widehat {PMQ}\) = \(\widehat {NQM}\). Chứng minh: MN = QP, MP = QN.
Xem đáp án
Xét hai tam giác vuông MNQ và QPM, ta có:
MQ là cạnh chung, \(\widehat {NQM}\) = \(\widehat {PMQ}\).
Suy ra ∆MNQ = ∆QPM (cạnh huyền – góc nhọn).
Do đó MN = QP, MP = QN (các cặp cạnh tương ứng).
Câu 8:
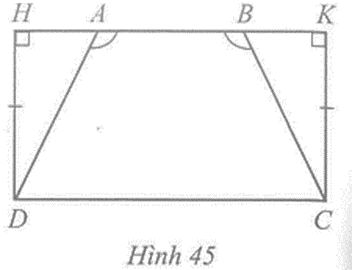
Cho Hình 45 có \(\widehat {AHD}\) = \(\widehat {BKC}\) = 90o, DH = CK, \(\widehat {DAB}\) = \(\widehat {CBA}\). Chứng minh AD = BC.
Xem đáp án
Ta có \(\widehat {DAH}\) + \(\widehat {DAB}\) = 180o (hai góc kề bù), suy ra \(\widehat {DAH}\) = 180o – \(\widehat {DAB}\)
\(\widehat {CBK}\) + \(\widehat {CBA}\) = 180o (hai góc kề bù), suy ra \(\widehat {CBK}\) = 180o – \(\widehat {CBA}\)
Mà \(\widehat {DAB}\) = \(\widehat {CBA}\)(giả thiết), suy ra \(\widehat {DAH}\) = \(\widehat {CBK}\).
Xét hai tam giác DAH và CBK, ta có:
DH = CK (giả thiết), \(\widehat {DAH}\) = \(\widehat {CBK}\).
Suy ra ∆DAH = ∆CBK (cạnh góc vuông – góc nhọn)
Do đó AD = BC (hai cạnh tương ứng).
Câu 9:
Cho tam giác ABC có \(\widehat B\) > \(\widehat C\). Tia phân giác góc BAC cắt BC tại điểm D.
Chứng minh \(\widehat {ADB}\) < \(\widehat {ADC}\)
Xem đáp án
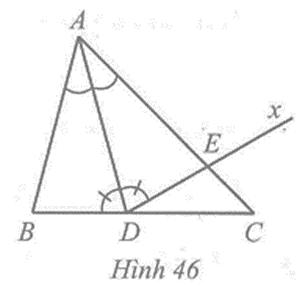
Xét hai tam giác ADB và ADC, ta có:
\(\widehat {DAB}\) + \(\widehat B\) + \(\widehat {ADB}\) = \(\widehat {DAC}\) + \(\widehat C\) + \(\widehat {ADC}\) = 180o (tổng ba góc của một tam giác)
Mà \(\widehat {DAB}\) = \(\widehat {DAC}\), \(\widehat B\) > \(\widehat C\) suy ra \(\widehat {ADB}\) < \(\widehat {ADC}\).
Câu 10:
Cho tam giác ABC có \(\widehat B\) > \(\widehat C\). Tia phân giác góc BAC cắt BC tại điểm D.
Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx}\) = \(\widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh ∆ABD = ∆AED, AB < AC.
Xem đáp án
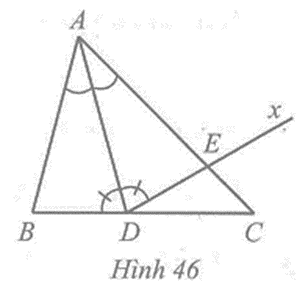
Xét hai tam giác ABD và AED, ta có:
\(\widehat {DAB}\) = \(\widehat {DAE}\) (vì AD là tia phân giác của góc BAC);
AD là cạnh chung;
\(\widehat {ADB}\) = \(\widehat {ADE}\) (giả thiết).
Suy ra ∆ABD = ∆AED (g.c.g).
Do đó:
AB = AE (hai cạnh tương ứng).
Vì E thuộc cạnh AC, E khác A và C nên AE < AC. Suy ra AB < AC.
Câu 11:
Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và NMP lầm lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ
Xem đáp án
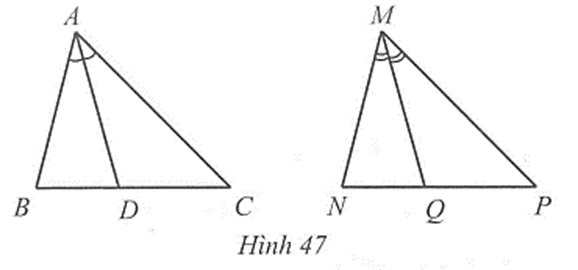
Vì AD là tia phân giác của góc BAC nên \(\widehat {BAD} = \frac{1}{2}\widehat {BAC}\);
MQ là tia phân giác của góc NMP nên \(\widehat {NMQ}\) = \[\frac{1}{2}\widehat {NMP}\];
Mà \(\widehat {BAC}\) = \(\widehat {NMP}\) (vì ∆ABC = ∆MNP), suy ra \(\widehat {BAD}\) = \(\widehat {NMQ}\)
Xét hai tam giác ABD và NMQ, ta có:
\(\widehat {BAD}\) = \(\widehat {NMQ}\), AB = MN, \(\widehat B\) = \(\widehat N\)(vì ∆ABC = ∆MNP).
Suy ra ∆ABD = ∆MNQ (g.c.g).
Do đó AD = MQ (hai cạnh tương ứng).
Câu 12:
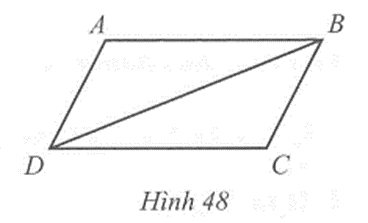
Cho Hình 48 có AB // CD, AD // BC. Chứng minh AB = CD, AD = BC
Xem đáp án
Xét hai tam giác ABD và CDB, ta có
\(\widehat {ABD} = \) \(\widehat {CDB}\)( hai góc so le trong);
BD là cạnh chung;
\(\widehat {ADB} = \) \(\widehat {CBD}\)( hai góc so le trong).
Suy ra ∆ABD = ∆CDB (g.c.g).
Do đó AB = CD, AD = BC (hai cạnh tương ứng).
Câu 13:
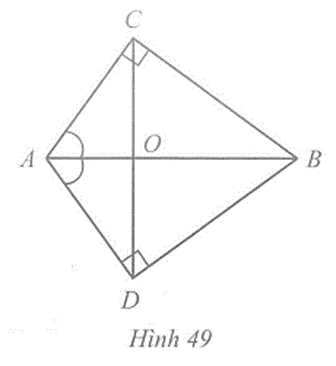
Trong Hình 49 có \(\widehat {ACB}\) = \(\widehat {ADB}\) = 90o, \(\widehat {BAC}\) = \(\widehat {BAD}\). Chứng minh:
BC = BD, AC = AD;
Xem đáp án
Xét hai tam giác vuông ABC và ABD, ta có:
AB là cạnh chung, \(\widehat {BAC}\) = \(\widehat {BAD}\) (giả thiết).
Suy ra ∆ABC = ∆ABD (cạnh huyền – góc nhọn).
Do đó BC = BD, AC = AD (các cặp cạnh tương ứng).
Câu 14:
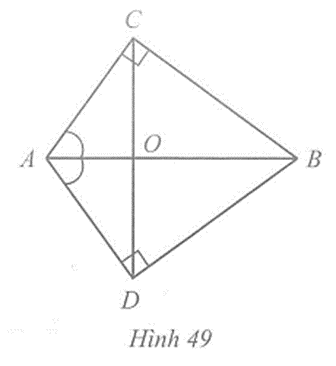
Trong Hình 49 có \(\widehat {ACB}\) = \(\widehat {ADB}\) = 90o, \(\widehat {BAC}\) = \(\widehat {BAD}\). Chứng minh:
OC = OD và OA vuông góc với CD.
Xem đáp án
Xét hai tam giác AOC và AOD, ta có
AO là cạnh chung, \(\widehat {OAC}\) = \(\widehat {OAD}\)( giả thiết)
AC = AD (chứng minh trên)
Suy ra ∆AOC = ∆AOD (c.g.c).
Do đó OC = OD (hai cạnh tương ứng), \(\widehat {AOC}\) = \(\widehat {AOD}\)(hai góc tương ứng)
Mà \(\widehat {AOC}\) + \(\widehat {AOD}\) = 180o (hai góc kề bù). Suy ra \(\widehat {AOC}\) = \(\widehat {AOD}\) = 90o
Vậy AO ⊥ CD.