Trắc nghiệm Toán 7 CTST Bài 4. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác có đáp án
Dạng 1: Các bài toán liên quan đến tính diện tích xung quanh, tổng diện tích các mặt và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có đáp án
-
673 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
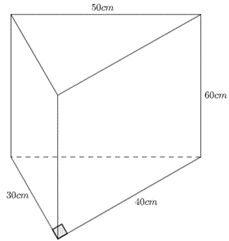
Xem đáp án
Hướng dẫn giải:
Thể tích của hình lăng trụ đứng tam giác đó là:
V = Sđáy. h = (\(\frac{1}{2}\). 30. 40 ). 60 = 36 000 (cm3)
Diện tích xung quanh của hình lăng trụ đứng tam giác đó là:
Sxq = Cđáy. h = (30 + 40 + 50). 60 = 7 200 (cm2)
Vậy thể tích của lăng trụ là 36 000 cm3 và diện tích xung quanh là 7 200 cm2.
Câu 2:
Xem đáp án
Hướng dẫn giải
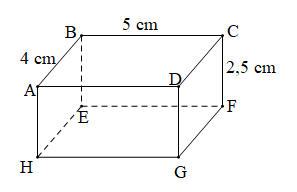Diện tích xung quanh của hình lăng trụ đứng này là:
Sxq = Cđáy. h = 2(AB + BC). CF = 2.(4 + 5). 2,5 = 45 (cm2).
Thể tích của hình lăng trụ đứng này là:
V = Sđáy. h = AB. BC. CF = 4. 5. 2,5 = 50 (cm3).
Vậy diện tích xung quanh của hình lăng trụ đứng ABCD.EFGH là 45 cm2.
Thể tích của hình lăng trụ đứng ABCD.EFGH là 50 cm3.
Câu 3:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Diện tích mặt đáy tam giác vuông ABC là:
SABC = \(\frac{1}{2}\)AB. AC = \(\frac{1}{2}\). 3. 4 = 6 (cm2)
Thể tích hình lăng trụ đứng ABC.A'B'C' là:
V = SABC. AA' = 6. 3 = 18 (cm3)
Câu 4:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Diện tích đáy hình thoi là:
Sđáy = \(\frac{1}{2}.3.4 = 6\)(cm2).
Thể tích của hình lăng trụ là:
V = Sđáy. h = 6. 5 = 30 (cm3).
Vậy ta chọn phương án A.
Câu 5:
Cho hình lăng trụ đứng có đáy là hình vuông, thể tích hình lăng trụ là 72 cm3, chiều cao là 8 cm. Độ dài cạnh đáy của lăng trụ là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Thể tích của hình lăng trụ được tính như sau:
V = Sđáy. H
Mà V = 72 (cm3) nên
Diện tích đáy là: Sđáy = 72 : 8 = 9 (cm2)
Gọi độ dài cạnh đáy là a (cm)
Do đó diện tích đáy là diện tích hình vuông cạnh a (cm).
Nên Sđáy = a. a = 9
Ta thấy 32 = 9 do đó a = 3 cm.
Vậy độ dài cạnh đáy của lăng trụ là 3 cm.
Câu 6:
Cho hình lăng trụ đứng tam giác có kích thước như hình vẽ.
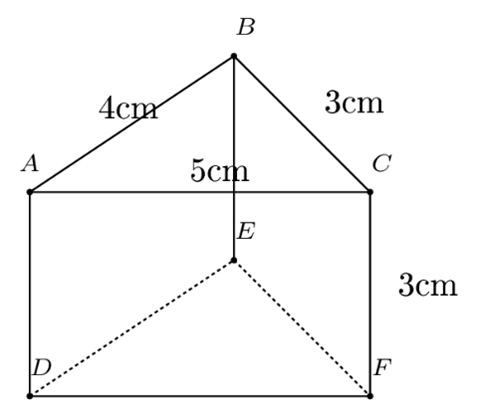
Diện tích xung quanh của hình lăng trụ đứng trên là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Diện tích xung quanh hình lăng trụ đứng đó là:
Sxq = (3 + 4 + 5). 3 = 12. 3 = 36 (cm2)
Vậy ta chọn phương án A.
Câu 7:
Cho hình lăng trụ đứng ABC.A’B’C’, AB = 6 cm; AC = 8 cm, BC = 10 cm, AA’ = 5 cm và thể tích là 120 cm3. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Thể tích của hình lăng trụ được tính như sau:
V = Sđáy. h
Do đó diện tích đáy là:
Sđáy = V : h = 120 : 5 = 24 (cm2).
Do đó phương án B và C là sai.
Diện tích xung quanh của hình lăng trụ đó là:
Sxq = (6 + 8 + 10).5 = 120 (cm2)
Do đó phương án A sai vì chưa đúng đơn vị diện tích.
Diện tích toàn phần của hình lăng trụ đó là:
Stp = Sxq + 2Sđáy = 120 + 2.24 = 168 (cm2)
Vậy ta chọn phương án D.
Câu 8:
Cho hình lăng trụ đứng ABCD.MNPQ có đáy hình thang AB // CD và AB = 4 cm; CD = 6 cm và chiều cao của hình thang là 5 cm, chiều cao của hình lăng trụ là 4 cm. Tính thể tích của hình lăng trụ?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Diện tích đáy hình thang của hình lăng trụ đó là:
Sđáy = \(\frac{1}{2}\) .(4 + 6). 5 = 25 (cm2)
Thể tích của lăng trụ đứng ABCD.MNPQ là:
V = Sđáy. h = 25. 4 = 100 (cm3)
Vậy ta chọn phương án C.
Câu 9:
Cho hình lăng trụ đứng ABC.DEF có Sxq = 120 cm2, AB = 6 cm; AC = 8 cm; AA’ = 5 cm. Độ dài cạnh BC là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:
Ta có Sxq = CABC. AA’ = 120 hay CABC.5 = 120
Do đó chu vi đáy của hình lăng trụ đứng đó là:
CABC = 120 : 5 = 24 (cm)
Mặt khác: CABC = AB + BC + AC
Suy ra BC = CABC – AB – AC = 24 – 6 – 8 = 10 (cm)
Vậy BC = 10 cm.
Câu 10:
Cho hình lăng trụ đứng ABCD.EFGH có đáy ABCD là hình chữ nhật, AB = 4 cm, BC = 5 cm, diện tích xung quanh là 45 cm2. Chiều cao AE của hình lăng trụ là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có chu vi của đáy hình chữ nhật là:
Cđáy = 2(AB + BC) = 2(4 + 5) = 18 (cm)
Diện tích xung quang của hình lăng trụ đó là:
Sxq = Cđáy. AE = 45
Suy ra AE = Sxq : Cđáy = 45 : 18 = 2,5 (cm)
Vậy chiều cao của hình lăng trụ là 2,5 cm.
Câu 11:
Cho hình lăng trụ đứng ABCD.EFGH có đáy ABCD là hình chữ nhật, AB = 4 cm; BC = 5 cm, chiều cao h = 2,5 cm. Tổng diện tích tất cả các mặt của hình lăng trụ là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Diện tích xung quanh của hình lăng trụ:
Sxq = 2(AB + BC). h = 2(4 + 5). 2,5 = 45 (cm2)
Diện tích đáy hình chữ nhật ABCD là:
Sđáy = 4.5 = 20 (cm2)
Tổng diện tích tất cả các mặt là:
S = Sxq + 2Sđáy = 45 + 2. 20 = 45 + 40 = 85 (cm2).
Vậy ta chọn phương án B.
Câu 12:
Cho hình lăng trụ đứng có độ dài cạnh bên là 20 cm và đáy là một hình thang cân. Biết hình thang có độ dài hai đáy lần lượt là 8 cm, 18 cm và chiều cao là 12 cm. và diện tích toàn phần (tổng diện tích tất cả các mặt) là 1 352 cm2. Độ dài cạnh bên của hình thang là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Diện tích đáy hình thang cân là:
\({S_{day}} = \frac{{\left( {8 + 18} \right).18}}{2} = 156\) (cm2)
Diện tích toàn phần của hình lăng trụ đó là:
Stp = Sxq + 2Sđáy do đó Sxq = Stp – 2Sđáy
Vậy diện tích xung quanh là:
Sxq = 1 352 – 2.156 = 1040 (cm2)
Mà Sxq = Cđáy. h
Suy ra Cđáy = 1040 : 20 = 52 (cm)
Gọi độ dài cạnh bên là a (cm)
Vì đáy là hình thang cân nên ta có chu vi đáy là:
Cđáy = 2a + 8 + 18
Mà theo bài Cđáy = 52 (cm)
Nên 2a + 8 + 18 = 52
Suy ra 2a = 52 – 8 – 18 = 26
Do đó a = 26 : 2 = 13
Vậy độ dài cạnh bên của hình thang là 13 cm.