15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án

Câu 1:

Điền vào chỗ trống sau: “Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với ... của cạnh đối diện”.

A. Trung trực;

B. Trung điểm;

C. Trọng tâm;

D. Giao điểm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.

Câu 2:

Điền vào chỗ trống sau: “Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua điểm ấy.”

A.

\frac{1}{3}

;

B.

\frac{1}{2}

;

C.

\frac{2}{3}

;

D.

\frac{1}{4}

.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua điểm ấy.

Câu 3:

Cho hình như bên dưới. Đường thẳng AM trong hình bên dưới là:

A. Đường trung trực của tam giác ∆ABC;

B. Đường trung tuyến của tam giác ∆ABC;

C. Đường cao của tam giác ∆ABC;

D. Đường phân giác của tam giác ∆ABC.

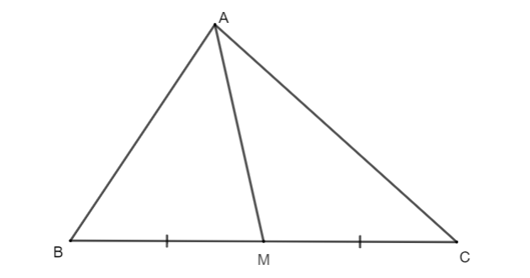
Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Tam giác ∆ABC có AM là đường trung tuyến từ đỉnh A nối với trung điểm của M cạnh BC.

Câu 4:

Giao điểm của ba đường trung trực của một tam giác:

A. Là trực tâm của tam giác đó;

B. Cách đều ba đỉnh của tam giác đó;

C. Là trọng tâm của tam giác đó;

D. Cách đều ba cạnh của tam giác đó.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Theo định nghĩa: Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm này được gọi là trọng tâm của tam giác.

Câu 5:

Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{A G}{A M}$ bằng :

A. $\frac{2}{3}$

B. $\frac{1}{3}$

C. $\frac{3}{4}$

D. $\frac{3}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

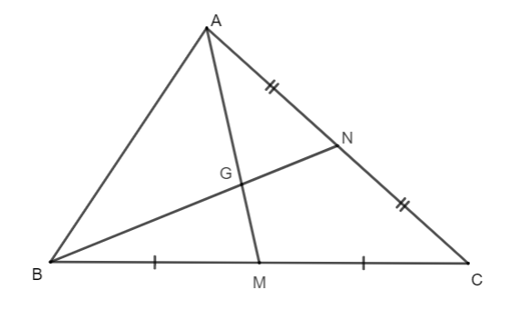
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G (ảnh 1)

Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{A G}{A M} = \frac{2}{3}$ .

Câu 6:

Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{G M}{A M}$ bằng :

A. $\frac{2}{3}$

B. $\frac{1}{3}$

C. $\frac{3}{4}$

D. $\frac{3}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

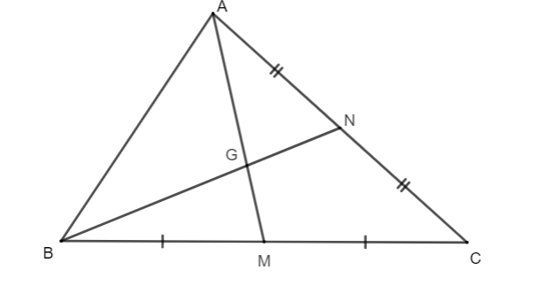
Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{A G}{A M} = \frac{2}{3}$ (1)

Ta có: AG = AM − GM

Thay vào (1) ta được:

$\frac{A M - G M}{A M} = \frac{2}{3}$

$\frac{A M}{A M}$ − $\frac{G M}{A M}$ = $\frac{2}{3}$

1 − $\frac{G M}{A M}$ = $\frac{2}{3}$

$\frac{G M}{A M}$ = 1− $\frac{2}{3}$ = $\frac{1}{3}$

Vậy $\frac{G M}{A M}$ = $\frac{1}{3}$ .

Câu 7:

Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{G M}{A G}$ bằng:

A. $\frac{2}{3}$

B. $\frac{1}{3}$

C. $\frac{3}{4}$

D. $\frac{1}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

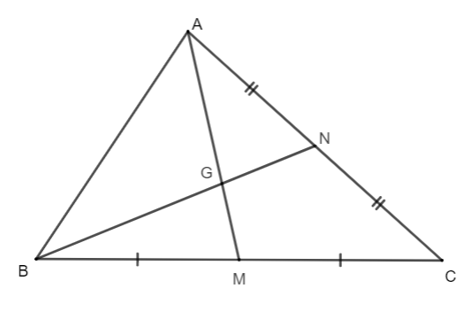
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau (ảnh 1)

Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{A G}{A M} = \frac{2}{3}$ và $\frac{G M}{A M} = \frac{1}{3}$

Ta có: $\frac{G M}{A M} : \frac{A G}{A M} = \frac{G M}{A G} = \frac{1}{3} : \frac{2}{3} = \frac{1}{2}$

Vậy $\frac{G M}{A G} = \frac{1}{2}$ .

Câu 8:

Cho tam giác ∆ABC cân tại A có hai điểm E và F lần lượt là trung điểm của AC và AB. Khi đó tam giác GBC là:

A. Tam giác cân;

B. Tam giác thường;

C. Tam giác đều;

D. Tam giác vuông.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

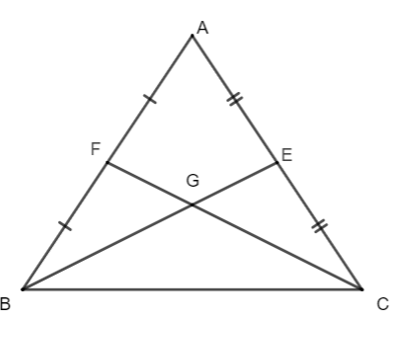
Cho tam giác ∆ABC cân tại A có hai điểm E và F lần lượt là trung điểm của AC và AB (ảnh 1)

Xét ∆ABC có:

BE là đường trung tuyến (E là trung điểm của AC);

CF là đường trung tuyến (F là trung điểm của AB);

BE và CF cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Ta có: ∆ABC cân tại A.

Suy ra AB = AC mà AB = 2AF; AC = 2AE

Do đó 2AF = 2AE hay AF = AE.

Xét ∆ABE và ∆ACF có:

$\hat{A}$ là góc chung;

AB = AC (∆ABC cân tại A);

AE = AF (cmt).

Do đó ∆ABE = ∆ACF (c.g.c).

Suy ra CF = BE.

Mà CF = $\frac{3}{2}$ CG ; BE = $\frac{3}{2}$ BG (G là trọng tâm của ∆ABC).

Nên $\frac{3}{2}$ CG = $\frac{3}{2}$ BG hay CG = BG.

Vậy tam giác ∆GBC là tam giác cân.

Câu 9:

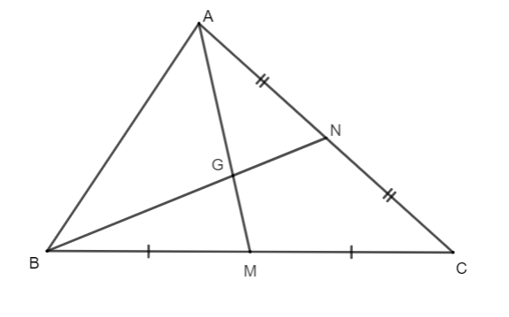
Cho hình vẽ như bên dưới. Biết AM = 12 cm. Tính chiều dài của đoạn thẳng AG.

A. 10 cm;

B. 4 cm;

C. 6 cm;

D. 8 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{A G}{A M} = \frac{2}{3}$

$\frac{A G}{12} = \frac{2}{3}$

AG = $\frac{12.2}{3}$ = $\frac{24}{3}$ = 8 (cm).

Vậy độ dài đoạn thẳng AG bằng 8 cm.

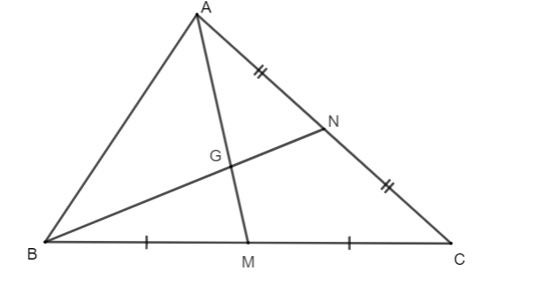
Câu 10:

Cho hình vẽ như bên dưới. Biết GN = 4 cm. Độ dài đoạn thẳng BN bằng:

A. 12 cm;

B. 10 cm;

C. 14 cm;

D. 16 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ABC có:

AM là đường trung tuyến (M là trung điểm của BC);

BN là đường trung tuyến (N là trung điểm của AC).

AM và BN cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{G N}{B N} = \frac{1}{3}$

BN = 3GN = 3 . 4 = 12 (cm)

Vậy độ dài đoạn thẳng AG bằng 12 cm.

Câu 11:

Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:

A. Tam giác vuông;

B. Tam giác vuông cân;

C. Tam giác thường;

D. Tam giác cân.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

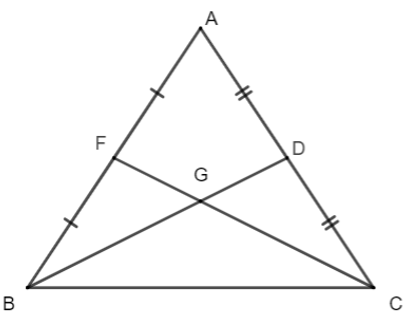
Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. (ảnh 1)

Xét ∆ABC có:

BE là đường trung tuyến (E là trung điểm của AC);

CF là đường trung tuyến (F là trung điểm của AB);

BE và CF cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra $\frac{B G}{B D} = \frac{2}{3}$ ; $\frac{C G}{C F} = \frac{2}{3}$

mà BD = CF (gt) nên BG = CG.

Do vậy FG = GD.

Xét ∆FGB và ∆DGC có:

BG = CG (cmt);

FG = GD (cmt);

$\hat{F G B}$ = $\hat{D G C}$ ( hai góc đối đỉnh).

Do đó ∆FGB = ∆DGC (c.g.c).

Suy ra BF = DC (hai cạnh tương ứng)

Ta có : AB = $\frac{1}{2}$ BF (F là trung điểm của AB);

AC= $\frac{1}{2}$ DC ( D là trung điểm của AC);

BF = DC (cmt).

Do đó AB = AC.

Vậy ∆ABC là tam giác cân tại A.

Câu 12:

Cho ∆ABC có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = CF và AG cắt BC tại E. Số đo là :

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

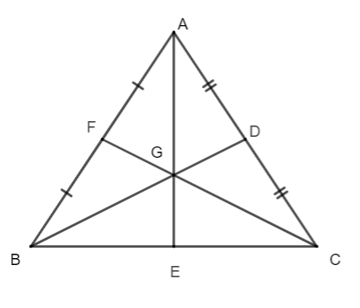
Cho ∆ABC có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = CF (ảnh 1)

Xét ∆ABC có:

BE là đường trung tuyến (E là trung điểm của AC);

CF là đường trung tuyến (F là trung điểm của AB);

BE và CF cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Suy ra AE là đường trung tuyến của ∆ABC.

Do vậy E là trung điểm của BC.

Ta có: $\frac{B G}{B D} = \frac{2}{3}$ ; $\frac{C G}{C F} = \frac{2}{3}$ (G là trọng tâm ∆ABC).

mà BD = CF (gt) nên BG = CG.

Do vậy FG = GD.

Xét ∆FGB và ∆DGC có:

BG = CG (cmt);

FG = GD (cmt);

$\hat{F G B}$ = $\hat{D G C}$ ( hai góc đối đỉnh).

Do đó ∆FGB = ∆DGC (c.g.c).

Suy ra BF = DC (hai cạnh tương ứng).

Ta có : AB = $\frac{1}{2}$ BF (F là trung điểm của AB);

AC= $\frac{1}{2}$ DC (D là trung điểm của AC);

BF = DC (cmt).

Do đó AB = AC.

Xét ∆AEB và ∆AEC ta có:

AB = AC (cmt);

AE là cạnh chung;

EB = EC (E là trung điểm của BC).

Do đó ∆AEB = ∆AEC (c.c.c).

Suy ra $\hat{A E C}$ = 90°.

Câu 13:

Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = 9 cm. Độ dài đoạn thẳng GF bằng:

A. 6 cm;

B. 3 cm;

C. 4 cm;

D. 5 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

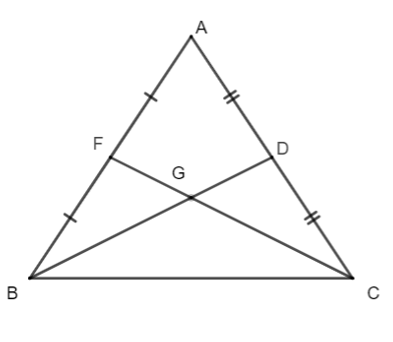
Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CF cắt nhau tại G. Biết (ảnh 1)

Xét ∆ABC có:

BE là đường trung tuyến (E là trung điểm của AC);

CF là đường trung tuyến (F là trung điểm của AB);

BE và CF cắt nhau tại G.

Do đó G là trọng tâm của ∆ABC.

Ta có: ∆ABC cân tại A.

Suy ra AB = AC mà AB = 2AF; AC = 2AD.

Do đó 2AF = 2AD hay AF = AD.

Xét ∆ABD và ∆ACF có:

$\hat{A}$ là góc chung;

AB = AC (∆ABC cân tại A);

AD = AF (cmt).

Do đó ∆ABD = ∆ACF (c.g.c)

Suy ra BD = CF.

Ta có : GF= $\frac{1}{3}$ CF ;

BD = CF = 9 (cm).

Do đó GF = $\frac{1}{3}$ . 9 = 3 (cm).

Vậy độ dài đoạn thẳng GF bằng 3 cm.

Câu 14:

Cho tam giác ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là:

A. Trọng tâm của ΔABD;

B. Trọng tâm của ΔABC;

C. Trực tâm của ΔABC;

D. Cách đều ba đỉnh của ΔABD.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

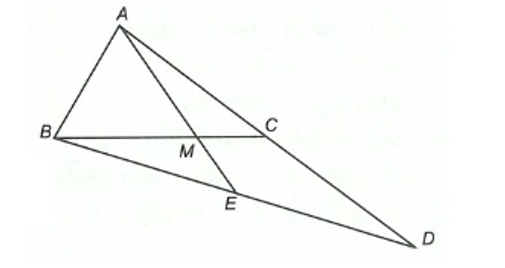
Cho tam giác ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. (ảnh 1)

Xét ΔABD có AC = CD.

Do đó BC là trung tuyến của ΔABD.

Mà BM = 2MC nên BM = $\frac{2}{3}$ BC.

Suy ra M là trọng tâm của ΔABD.

Câu 15:

Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:

A. Trọng tâm của ΔABC;

B. Trực tâm của ΔABC;

C. Cách đều ba đỉnh của ΔABC;

D. Cách đều ba cạnh của ΔABC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

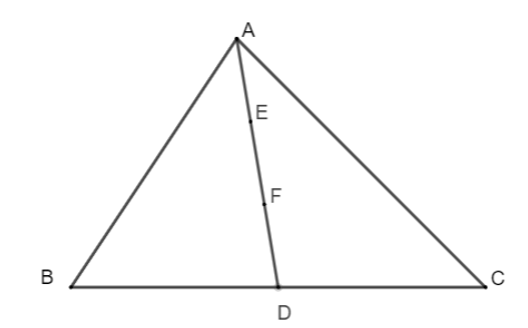
Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F (ảnh 1)

Ta có: AD = AE + EF + FD mà AE = EF = FD nên AD = 3AE.

Suy ra AE = EF = FD = $\frac{1}{3}$ AD.

Do đó AF = $\frac{2}{3}$ AD.

Vì AD là đường trung tuyến và AF = $\frac{2}{3}$ AD nên F là trọng tâm của ΔABC.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 7 Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án

Trắc nghiệm Toán 7 Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương