Trắc nghiệm Toán 7 CD Bài 3. Phép cộng, phép trừ đa thức một biến (Phần 2) có đáp án
Trắc nghiệm Toán 7 CD Bài 3. Phép cộng, phép trừ đa thức một biến (Thông dụng) có đáp án
-
357 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho: P(x) = 2x4 – x2 + x – 2; Q(x) = 3x4 + x3 + 2x2 + x + 1.
Tìm đa thức M(x) = Q(x) + P(x) và hệ số tự do của M(x)
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
M(x) = Q(x) + P(x)
= (3x4 + x3 + 2x2 + x + 1) + (2x4 – x2 + x – 2)
= 3x4 + x3 + 2x2 + x + 1 + 2x4 – x2 + x – 2
= (3x4 + 2x4) + x3 + (2x2 – x2) + (x + x) + (1 – 2)
= 5x4 + x3 + x2 + 2x – 1
Số hạng không chứa biến là – 1, nên hệ số tự do là – 1.
Vậy M(x) = 5x4 + x3 + x2 + 2x – 1, hệ số tự do là – 1.
Câu 2:
Cho đa thức A(x) = 5x4 – x3 + 2x2 + 4 và B(x) = 5x4 – 3x3 + x – 7.
Biết F(x) = A(x) – B(x). Bậc và hệ số cao nhất của đa thức F(x) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
F(x) = A(x) – B(x)
= (5x4 – x3 + 2x2 + 4) – (5x4 – 3x3 + x – 7)
= 5x4 – x3 + 2x2 + 4 – 5x4 + 3x3 – x + 7
= (5x4 – 5x4) + (– x3 + 3x3) + 2x2 – x + (4 + 7)
= 2x3 + 2x2 – x + 11
Vậy F(x) = 2x3 + 2x2 – x + 11 có bậc 3, hệ số cao nhất là 2.
Câu 3:
Cho 3 đa thức:
A(x) = x4 + 2x3 + 2x2 – x – 2; B(x) = 3x4 – x3 + x2 – 2x + 1; C(x) = – 3x4 + x3 – 2x + 1.
Biết N(x) = B(x) + C(x) – A(x). Đa thức N(x) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
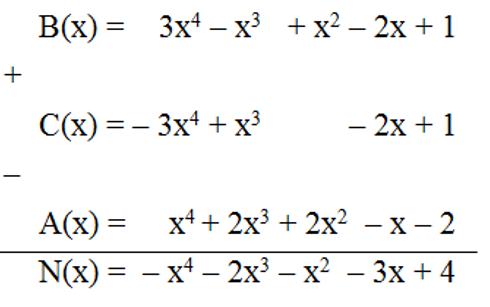
Câu 4:
Cho: P(x) = 2x4 – x2 + x – 2; Q(x) = 3x4 + x3 + 2x2 + x + 1.
Biết H(x) + P(x) = Q(x). Đa thức H(x) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
H(x) + P(x) = Q(x)
nên H(x) = Q(x) – P(x)
= (3x4 + x3 + 2x2 + x + 1) – (2x4 – x2 + x – 2)
= 3x4 + x3 + 2x2 + x + 1 – 2x4 + x2 – x + 2
= (3x4 – 2x4) + x3 + (2x2 + x2) + (x – x) + (1 + 2)
= x4 + x3 + 3x2 + 3
Vậy H(x) = x4 + x3 + 3x2 + 3.
Câu 5:
Cho 3x4 + 5x3 – 5x2 + 5x + 1 – P(x) = 2x4 + 2x3 – x2 + x – 4. Tìm P(x)?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
3x4 + 5x3 – 5x2 + 5x + 1 – P(x) = 2x4 + 2x3 – x2 + x – 4
P(x) = (3x4 + 5x3 – 5x2 + 5x + 1) – (2x4 + 2x3 – x2 + x – 4)
P(x) = 3x4 + 5x3 – 5x2 + 5x + 1 – 2x4 – 2x3 + x2 – x + 4
P(x) = (3x4 – 2x4) + (5x3 – 2x3) + (– 5x2 + x2) + (5x – x) + (1 + 4)
P(x) = x4 + 3x3 – 4x2 + 4x + 5
Câu 6:
Cho Q(x) – (x5 + 2x3 – 2 + x) = 3x3 + 2x2 – 1. Tìm Q(x) rồi sắp xếp theo lũy thừa giảm dần của biến.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Q(x) – (x5 + 2x3 – 2 + x) = 3x3 + 2x2 – 1
Q(x) = 3x3 + 2x2 – 1 + (x5 + 2x3 – 2 + x)
Q(x) = 3x3 + 2x2 – 1 + x5 + 2x3 – 2 + x
Q(x) = (3x3 + 2x3) + 2x2 + (– 1 – 2) + x5 + x
Q(x) = 5x3 + 2x2 – 3 + x5 + x
Q(x) = x5 + 5x3 + 2x2 + x – 3.
Câu 7:
Hai đa thức P(x) và Q(x) nào dưới đây thỏa mãn P(x) – Q(x) = x3 – 3x2 + x?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Thử đáp án A, ta có:
P(x) – Q(x) = (x5 + x3 + 5x2 + 2x – 1) – (x4 + 8x2 + x + 1)
= x5 + x3 + 5x2 + 2x – 1 – x4 – 8x2 – x – 1
= x5 – x4 + x3 + (5x2 – 8x2) + (2x – x) + (– 1 – 1)
= x5 – x4 + x3 – 3x2 + x – 2
Do đó đáp án A không đúng.
Thử đáp án B, ta có:
P(x) – Q(x) = (x4 + x3 + 5x2 + 2x – 1) – (x4 + 8x2 – x + 1)
= x4 + x3 + 5x2 + 2x – 1 – x4 – 8x2 + x – 1
= (x4 – x4) + x3 + (5x2 – 8x2) + (2x + x) + (– 1 – 1)
= x3 – 3x2 + 3x – 2
Do đó đáp án B không đúng.
Thử đáp án C, ta có:
P(x) – Q(x) = (x4 + x3 + 5x2 + 2x + 1) – (x4 + 2x3 + 8x2 – x + 1)
= x4 + x3 + 5x2 + 2x + 1 – x4 – 2x3 – 8x2 + x – 1
= (x4 – x4) + (x3 – 2x3) + (5x2 – 8x2) + (2x + x) + (1 – 1)
= – x3 – 3x2 + 3x
Do đó đáp án C không đúng.
Thử đáp án D, ta có:
P(x) – Q(x) = (x5 + x3 + 5x2 + 2x – 1) – (x5 + 8x2 + x – 1)
= x5 + x3 + 5x2 + 2x – 1 – x5 – 8x2 – x + 1
= (x5 – x5) + x3 + (5x2 – 8x2) + (2x – x) + (– 1 + 1)
= x3 – 3x2 + x
Vậy đáp án đúng là D.