Trắc nghiệm Toán 7 KNTT Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc có đáp án
Trắc nghiệm Toán 7 KNTT Dạng 1. Nhận biết hai góc kề nhau, bù nhau, kề bù và đối đỉnh có đáp án
-
943 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Quan sát hình vẽ sau và cho biết:
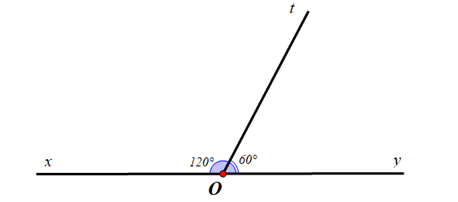
Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\)có kề với nhau không? Vì sao?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: \(\widehat {xOt},\widehat {tOy}\)là hai góc có một cạnh chung Ot và hai cạnh Ox, Oy nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung Ot.
Suy ra \(\widehat {xOt},\widehat {tOy}\)là hai góc kề nhau.
Câu 2:
Quan sát hình vẽ sau và cho biết:
Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\)có bù với nhau không? Vì sao?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Có \(\widehat {xOt} = 12{0^o},\widehat {tOy} = 6{0^o}\)
Suy ra \(\widehat {xOt} + \widehat {tOy} = {120^o} + {60^o} = {180^o}\)
Khi đó \(\widehat {xOt},\widehat {tOy}\) là hai góc bù nhau.
Câu 3:
Quan sát hình vẽ sau và cho biết:
Hai góc \(\widehat {xOt}\) và \(\widehat {tOy}\)có kề bù với nhau không? Vì sao?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì \(\widehat {xOt},\widehat {tOy}\) là hai góc vừa kề nhau vừa bù nhau nên \(\widehat {xOt},\widehat {tOy}\) là hai góc kề bù.
Câu 4:
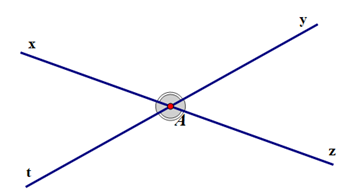
Hai đường thẳng xz và yt cắt nhau tại A như hình vẽ bên, hãy xác định các cặp góc đối đỉnh có trong hình vẽ.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
- Vì hai đường thẳng xz và yt cắt nhau tại A nên ta có: Hai tia Ax và Az đối nhau; hai tia Ay và At đối nhau.
- Xét hai góc \(\widehat {xAt}\) và \(\widehat {yAz}\) có:
+ Chung đỉnh A.
+ Tia Ax là tia đối của tia Az; tia At là tia đối của tia Ay.
Do đó \(\widehat {xAt}\) và \(\widehat {yAz}\) là hai góc đối đỉnh.
- Xét hai góc \(\widehat {xAy}\) và \(\widehat {tAz}\) có:
+ Chung đỉnh A.
+ Tia Ax là tia đối của tia Az; tia Ay là tia đối của tia At.
Do đó \(\widehat {xAy}\) và \(\widehat {tAz}\) là hai góc đối đỉnh.
Vậy ta có hai cặp góc đối đỉnh là: \(\widehat {xAt}\) và \(\widehat {yAz}\); \(\widehat {xAy}\) và \(\widehat {tAz}\).
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Hai góc được đánh dấu ở đáp án C là \(\widehat {xOy}\) và \(\widehat {zOt}\).
Ta thấy \(\widehat {xOy}\) và \(\widehat {zOt}\) là hai góc không có cạnh chung.
Do đó hai góc \(\widehat {xOy}\) và \(\widehat {zOt}\) không là hai góc kề nhau.
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Hai góc bù nhau là hai góc có tổng bằng 180°.
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
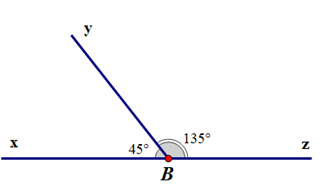
+ Ta có: \(\widehat {xBy},\widehat {yBz}\)là hai góc có một cạnh chung Oy và hai cạnh Bx, Bz nằm trên hai nửa mặt phẳng đối nhau bờ chứa cạnh chung By.
Suy ra \(\widehat {xBy},\widehat {yBz}\) là hai góc kề nhau.
Suy ra khẳng định A đúng.
+ Có \(\widehat {xBy} = {45^o},\widehat {yBz} = {135^o}\)
Suy ra \(\widehat {xBy} + \widehat {yBz} = {45^o} + {135^o} = {180^o}\)
Khi đó \(\widehat {xBy},\widehat {yBz}\) là hai góc bù nhau.
Suy ra khẳng định B đúng.
+ Vì \(\widehat {xBy},\widehat {yBz}\) là hai góc vừa kề nhau vừa bù nhau nên \(\widehat {xBy},\widehat {yBz}\) là hai góc kề bù.
Suy ra khẳng định C đúng.
+ Hai góc \(\widehat {xBy}\) và \(\widehat {yBz}\) có tia Bx là tia đối của tia Bz. Tuy nhiên tia By của \(\widehat {xBy}\)không là tia đối với tia nào của \(\widehat {yBz}\).
Suy ra \(\widehat {xBy}\) và \(\widehat {yBz}\) không là hai góc đối đỉnh.
Vậy khẳng định D sai.
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
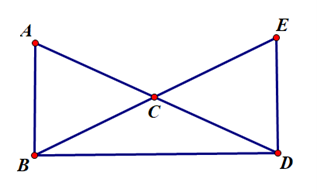
\(\widehat {ACB}\) và \(\widehat {ECD}\) là hai góc đối đỉnh vì hai góc có chung đỉnh C và cạnh CA thuộc tia đối của cạnh CD; cạnh CB thuộc tia đối của cạnh CE.
Câu 9:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
+ Hai đường thẳng cắt nhau tạo thành hai cặp góc đối đỉnh.
Ví dụ hai đường thẳng xx’ và yy’ cắt nhau tại A sẽ tạo thành hai cặp góc đối đỉnh là \(\widehat {xAy}\) và \(\widehat {x'Ay'}\); \(\widehat {xAy'}\) và \(\widehat {x'Ay}\).
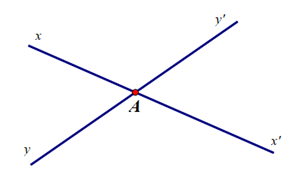
Do đó khẳng định D đúng.
+ Khẳng định A, B, C sai vì:
Hai góc có tổng bằng 180° là hai góc bù nhau.
Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía đối với đường thẳng chứa cạnh chung đó.
Câu 10:
Điền vào chỗ trống trong phát biểu sau:
“Hai góc có mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc…”
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Hai góc có mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh.
Câu 11:
Cho hình vẽ dưới đây, khẳng định nào sau đây sai?
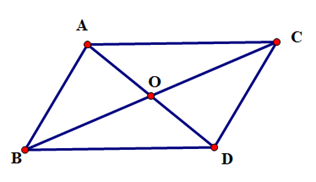
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Ta có \(\widehat {BAD}\) và \(\widehat {DAC}\) là hai góc kề nhau nhưng không bù nhau.
Suy ra \(\widehat {BAD}\) và \(\widehat {DAC}\) không là hai góc kề bù.
Do đó khẳng định C sai.
Câu 12:
Cho các khẳng định sau:
(I). Hai góc đối đỉnh thì bằng nhau.
(II). Hai góc bằng nhau thì đối đỉnh.
(III). Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Số khẳng định đúng là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Hai góc đối đỉnh thì bằng nhau nhưng hai góc bằng nhau thì chưa chắc đã đối đỉnh. Dưới đây là một số ví dụ về trường hợp hai góc bằng nhau nhưng không đối đỉnh:
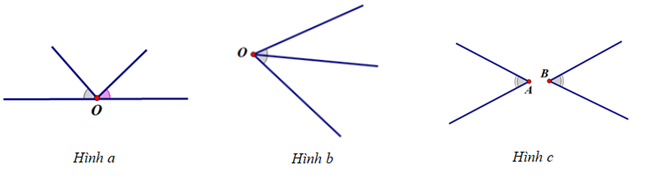
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
Do đó các khẳng định (I), (III) đúng. Khẳng định (II) sai.
Vậy có 2 khẳng định đúng.
Câu 13:
Cho hình vẽ, số cặp góc kề bù có trong hình vẽ bên là:
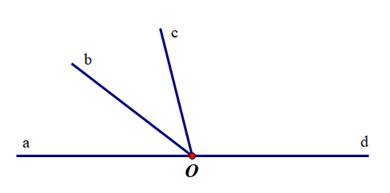
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Các cặp góc kề bù có trong hình vẽ trên là: \(\widehat {aOb}\) và \(\widehat {bOd}\); \(\widehat {aOc}\) và \(\widehat {cOd}\).
Vậy có 2 cặp góc kề bù với nhau.
Câu 14:
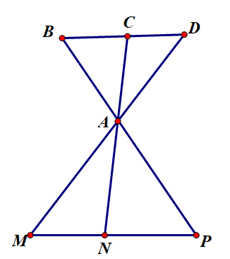
Cho hình vẽ sau, số cặp góc đối đỉnh có trong hình vẽ là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Các cặp góc đối đỉnh có trong hình vẽ trên là: \(\widehat {BAC}\) và \(\widehat {NAP}\); \(\widehat {CAD}\) và \(\widehat {MAN}\); \(\widehat {BAD}\) và \(\widehat {MAP}\).
Vậy có 3 cặp góc đối đỉnh có trong hình vẽ.
