Trắc nghiệm Toán 7 Bài 2. Tia phân giác có đáp án (Nhận biết)
-
426 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ
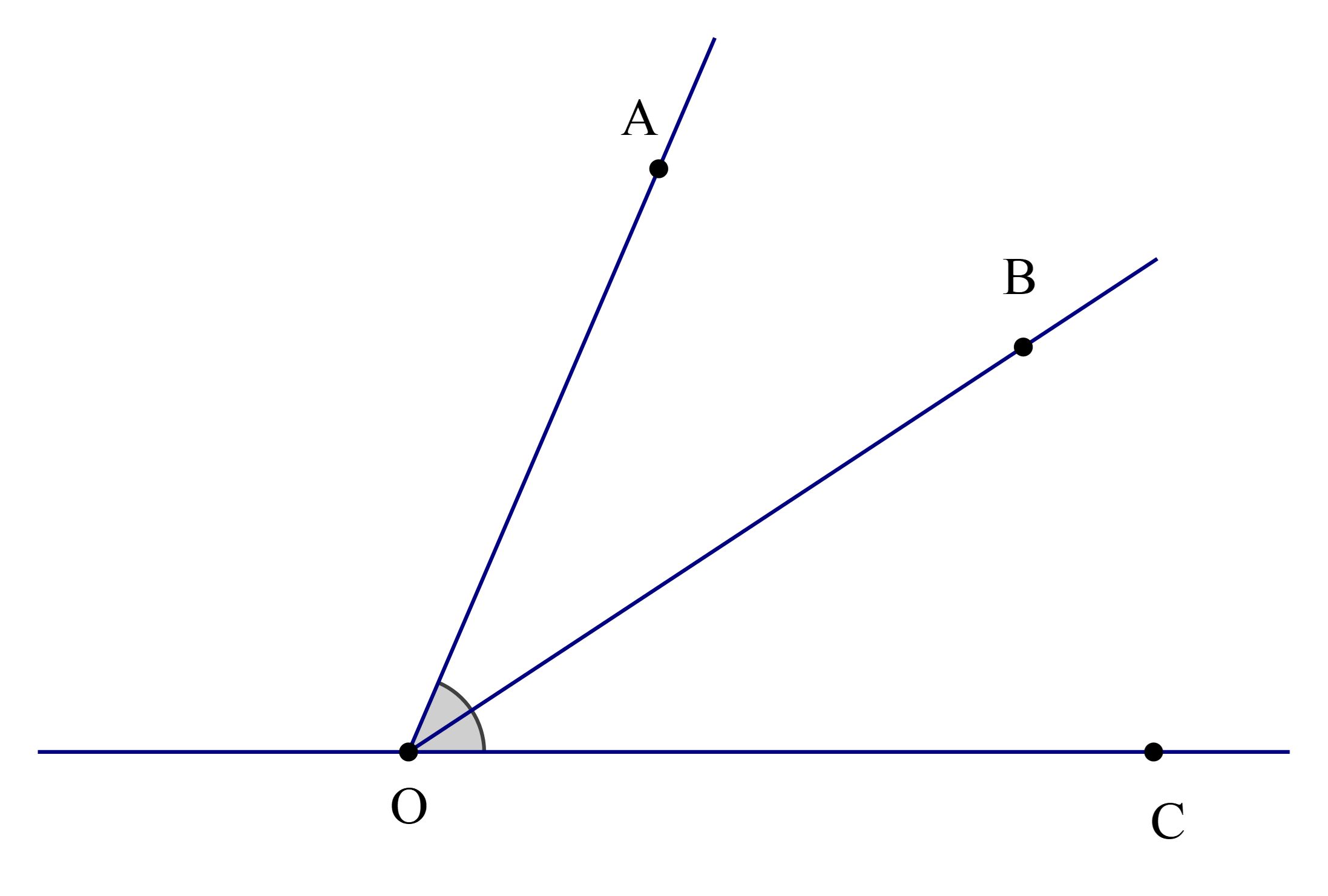
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì tia OB nằm giữa hai tia OA và OC nên tạo thành hai góc tương ứng là \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOC}}}.\)
Mà \(\widehat {{\rm{AOB}}} = \widehat {{\rm{BOC}}}.\)
Do đó OB là tia phân giác của \(\widehat {{\rm{AOC}}}.\)
Vậy ta chọn phương án B.
Câu 2:
Chọn phát biểu đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Tia phân giác của một góc là tia xuất phát từ đỉnh của góc, đi qua một điểm trong của góc và tạo với hai cạnh của góc đó hai góc bằng nhau. Do đó:
- Tia phân giác của một góc tạo với hai cạnh của góc đó sẽ tạo thành hai góc kề nhau nên phương án D sai.
- Tia phân giác của một góc tạo với hai cạnh của góc đó hai góc bằng nhau nên phương án A và B sai; phương án C đúng.
Vậy ta chọn phương án C.
Câu 3:
Tia Oz là tia phân giác của \(\widehat {{\rm{xOy}}}\), biết rằng \(\widehat {{\rm{xOz}}} = 40^\circ \). Số đo của \(\widehat {{\rm{yOz}}}\) là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
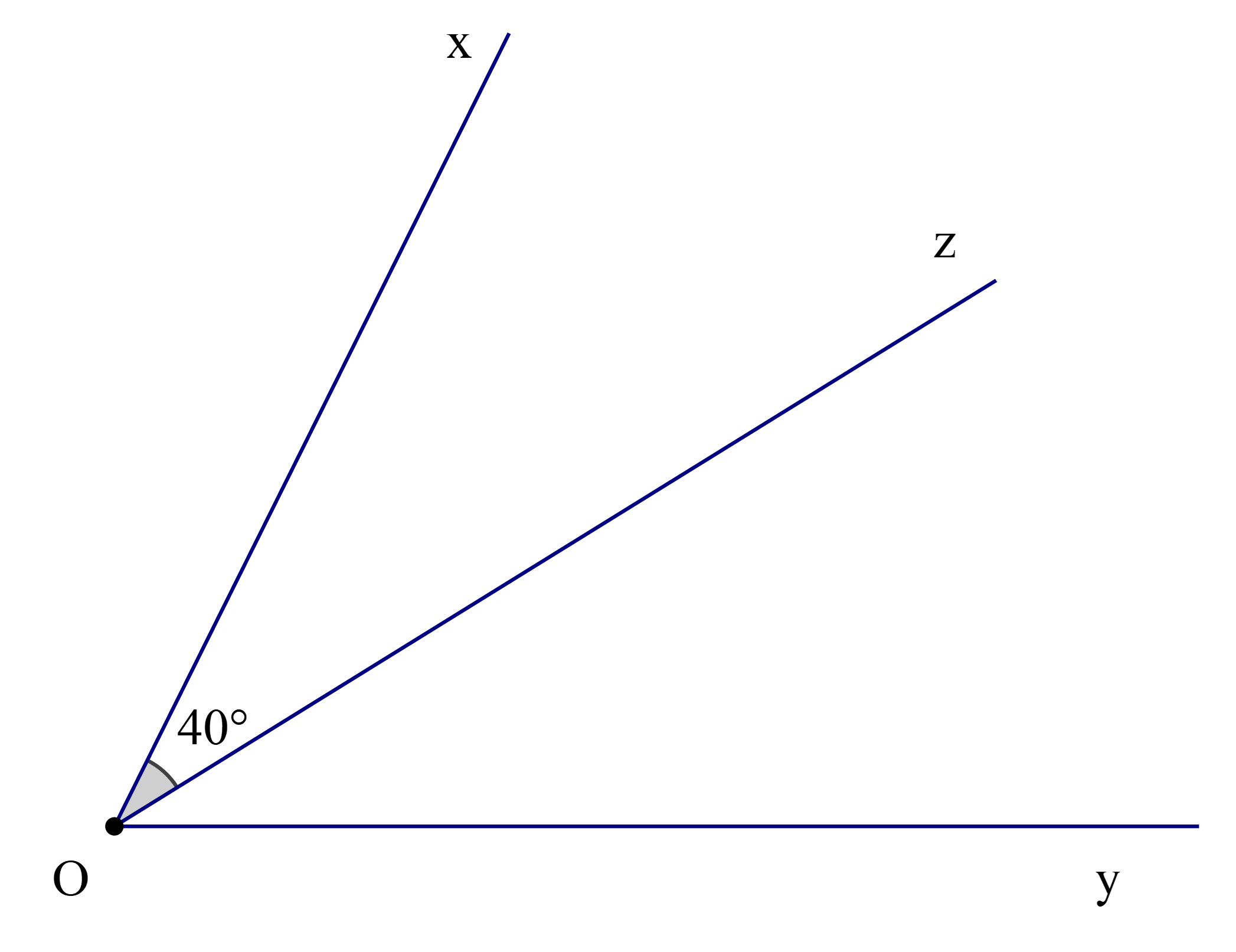
Theo bài ta có: Oz là tia phân giác của \(\widehat {{\rm{xOy}}}\)
Nên \(\widehat {{\rm{xOz}}} = \widehat {{\rm{zOy}}}\) (tính chất tia phân giác của một góc)
Mà \(\widehat {{\rm{xOz}}} = 40^\circ \)
Suy ra \(\widehat {{\rm{yOz}}} = 40^\circ \)
Vậy ta chọn phương án B.
Câu 4:
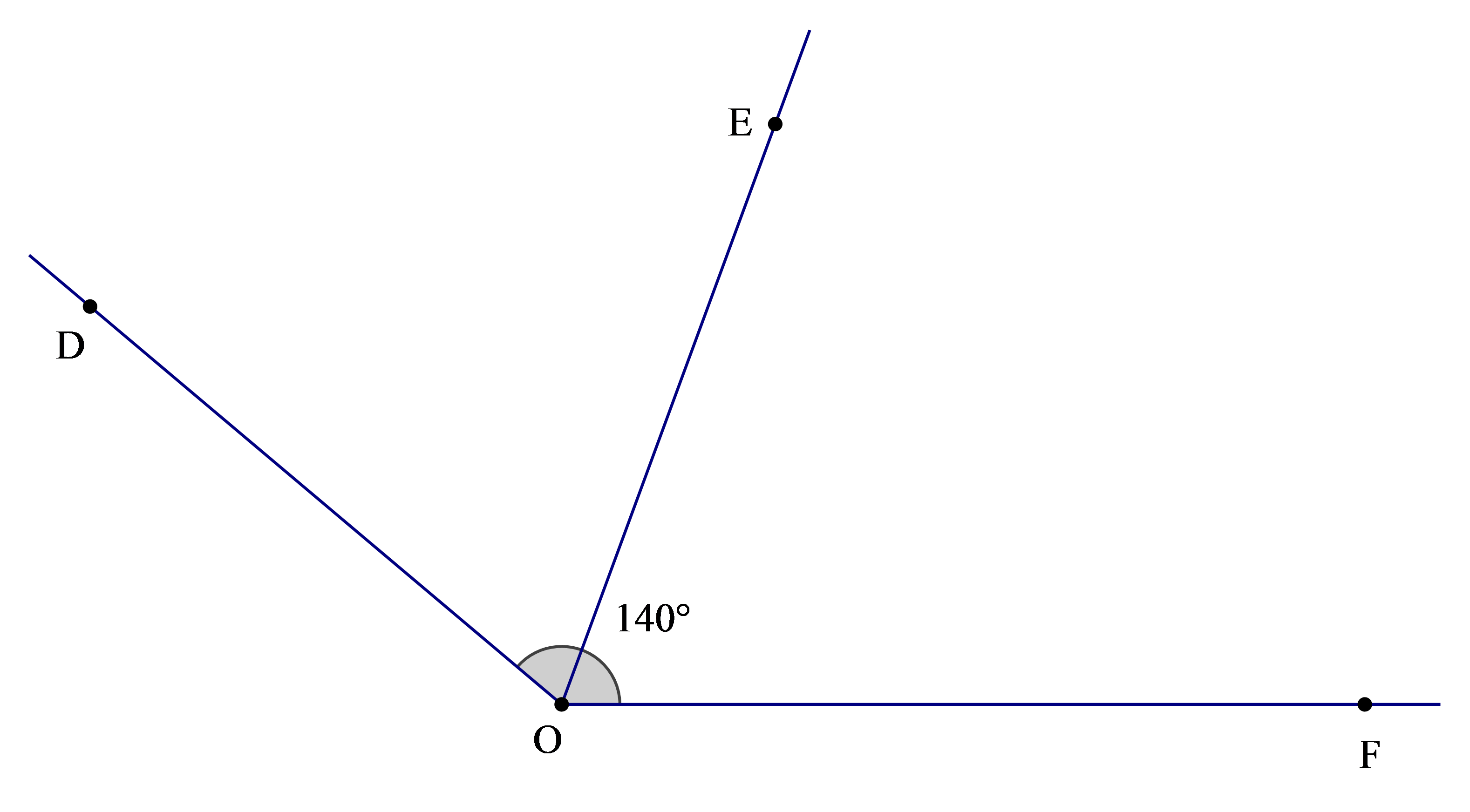
Cho \(\widehat {{\rm{DOF}}} = 140^\circ \), biết rằng OE là tia phân giác của \(\widehat {{\rm{DOF}}}\). Số đo của \(\widehat {EOF}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
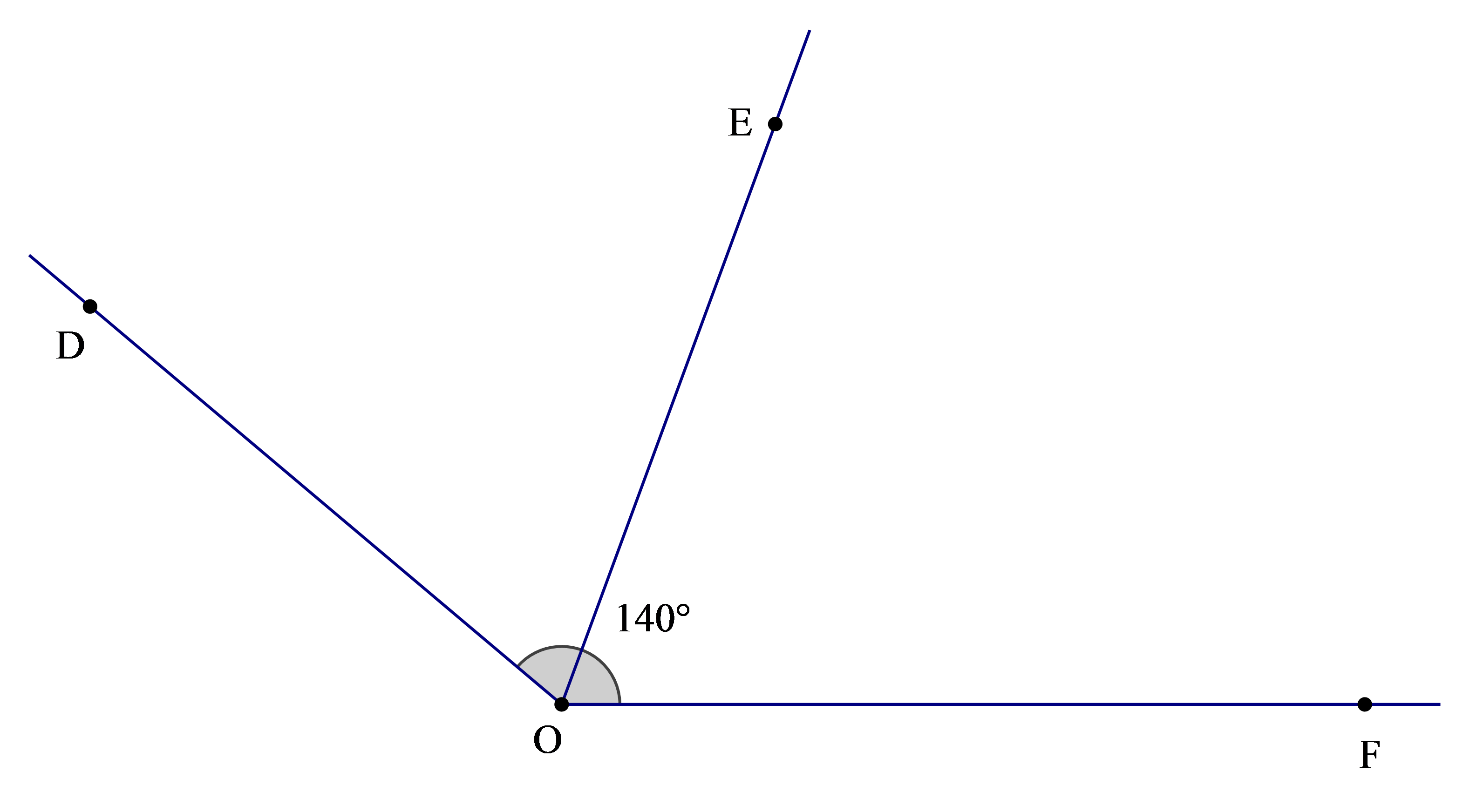
Theo bài ta có: OE là tia phân giác của \(\widehat {{\rm{DOF}}}\)
Nên \(\widehat {{\rm{DOE}}} = \widehat {EOF}\) (tính chất đường phân giác của một góc) (1)
Ta lại có \(\widehat {{\rm{DOE}}} + \widehat {EOF} = \widehat {{\rm{DOF}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{DOE}}} = \widehat {EOF} = \frac{1}{2}\widehat {{\rm{DOF}}} = \frac{1}{2}.140^\circ = 70^\circ \)
Do đó \(\widehat {EOF} = 70^\circ \)
Vậy ta chọn phương án C.
Câu 5:
Cho \(\widehat {{\rm{xOy}}} = 90^\circ \), kẻ Oz sao cho Oy là phân giác của \(\widehat {xOz}\). Khi đó \(\widehat {xOz}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Theo bài tia Oy là phân giác của \(\widehat {xOz}\)
Nên \(\widehat {{\rm{yOz}}} = \widehat {{\rm{xOy}}} = 90^\circ \)(tính chất tia phân giác của một góc)
Ta có \(\widehat {{\rm{xOy}}} + \widehat {{\rm{yOz}}} = \widehat {{\rm{xOz}}}\) (hai góc kề nhau)
Hay \(90^\circ + 90^\circ = \widehat {{\rm{xOz}}}\)
Suy ra \(\widehat {{\rm{xOz}}} = 180^\circ \)
Do đó \(\widehat {{\rm{xOz}}}\) là góc bẹt
Vậy ta chọn phương án D.