Trắc nghiệm Toán 7 KNTT Bài ôn tập cuối chương 4 (Nhận biết) có đáp án
-
461 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cặp tam giác nào sau đây bằng nhau?
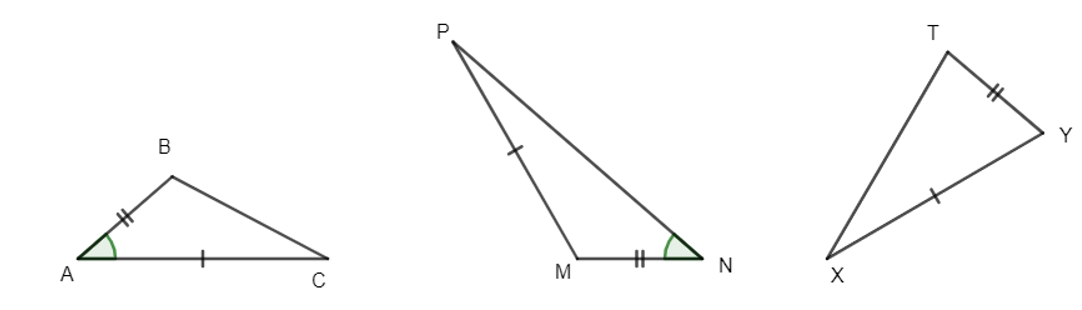
Khẳng định nào sau đây đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
⦁ Xét ∆ABC và ∆MNP, có:
AB = MN (giả thiết)
AC = MP (giả thiết)
(giả thiết)
Tuy nhiên hai góc và không xen giữa hai cạnh đã cho.
Suy ra ∆ABC và ∆MNP không bằng nhau. Do đó A sai.
⦁ Xét ∆MNP và ∆XYT, có:
MN = YT (giả thiết)
MP = XY (giả thiết)
Chưa đủ điều kiện để suy ra ∆MNP và ∆XYT bằng nhau. Do đó B sai.
⦁ Xét ∆ABC và ∆XYT, có:
AB = YT (giả thiết)
AC = XY (giả thiết)
Chưa đủ điều kiện để suy ra ∆ABC và ∆XYT bằng nhau. Do đó C sai.
Vì vậy không có cặp tam giác nào bằng nhau.
Vậy chọn đáp án D.
Câu 2:
Cho ∆ABC vuông tại B và ∆DEF vuông tại E có AB = DE và BC = EF. Khi đó ∆ABC = ∆DEF theo trường hợp:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆ABC và ∆DEF, có:
.
AB = DE (giả thiết)
BC = EF (giả thiết)
Do đó ∆ABC = ∆DEF (c.g.c)
Vậy ta chọn phương án C.
Câu 3:
Cho ∆MNP vuông tại P và ∆XYZ vuông tại Z có MP = XZ. Để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện gì?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta thấy MP, XZ lần lượt là cạnh góc vuông của ∆MNP và ∆XYZ.
Do đó để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện hai cạnh huyền của hai tam giác đó bằng nhau. Nghĩa là, MN = XY.
Vậy ta chọn phương án A.
Câu 4:
Phát biểu nào sau đây đúng nhất?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
⦁ Tam giác cân là tam giác có hai cạnh bằng nhau.
Suy ra phương án A đúng.
⦁ Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
Suy ra phương án B đúng.
⦁ Tam giác đều là tam giác có ba cạnh bằng nhau.
Suy ra phương án C đúng.
Vậy ta chọn phương án D.
Câu 5:
Phát biểu nào dưới đây đúng nhất?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Phương án A: Phát biểu của trường hợp cạnh góc vuông – góc nhọn kề (hay g.c.g).
Phương án B: Phát biểu của trường hợp cạnh huyền – cạnh góc vuông.
Phương án C: Phát biểu của trường hợp cạnh huyền – góc nhọn.
Vậy ta chọn phương án D.
Câu 6:
Cho ∆ABC có AB = BC = 5 cm và . Khi đó ∆ABC là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Một tam giác có hai cạnh bằng nhau là tam giác cân.
Tam giác cân có một góc bằng 60° là tam giác đều.
Vì vậy ∆ABC là tam giác đều.
Vậy ta chọn phương án A.
Câu 7:
Cho ∆MNP cân tại M và . Số đo của bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Vì ∆MNP cân tại M nên ta có .
∆MNP có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Khi đó .
Vì vậy .
Vậy ta chọn phương án C.
Câu 8:
Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
⦁ Xét phương án A:
Xét ∆ABC và ∆A’B’C’, có:
.
AB = A’B’ (giả thiết)
BC = B’C’ (giả thiết)
Do đó ∆ABC = ∆A’B’C’ (c.g.c)
Vì vậy phương án A có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án B:
Xét ∆A’B’C’ và ∆ABC, có:
.
B’C’ = BC (giả thiết)
(giả thiết)
Do đó ∆A’B’C’ = ∆ABC (g.c.g)
Vì vậy phương án B có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án C:
Xét ∆ABC và ∆A’B’C’, có:
.
AC = A’C’ (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆A’B’C’ (cạnh huyền – góc nhọn)
Vì vậy phương án C có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án D:
Xét ∆ABC và ∆A’B’C’, có:
.
(giả thiết)
(giả thiết)
Do đó ∆ABC và ∆A’B’C’ không bằng nhau do không có trường hợp bằng nhau góc – góc – góc.
Vậy ta chọn phương án D.
Câu 9:
Tổng ba góc trong một tam giác bất kì luôn bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì tổng ba góc trong một tam giác luôn bằng 180°.
Nên ta chọn phương án B.
Câu 10:
Đường trung trực của một đoạn thẳng là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.
Vậy ta chọn phương án C.