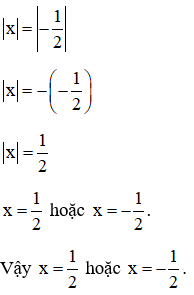15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 Bài 3. Giá trị tuyệt đối của một số thực có đáp án

Trắc nghiệm Toán 7 Bài 3. Giá trị tuyệt đối của một số thực có đáp án

Đề số 1

Trắc nghiệm Toán 7 Bài 3. Giá trị tuyệt đối của một số thực có đáp án

682 lượt thi
15 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Trên trục số, khoảng cách từ điểm – 3 đến điểm gốc 0 là:

A. – 3;

B. 3;

C. 1,5;

D. 6;

Xem đáp án

Đáp án đúng là: B.

Điểm A biểu diễn số – 3 trên trục số như sau:

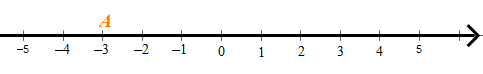
Khoảng cách từ điểm A đến gốc 0 là 3 đơn vị.

Câu 2:

Chọn phát biểu đúng.

A. Giá trị tuyệt đối của một số luôn là một số dương;

B. Giá trị tuyệt đối của một số luôn là một số không âm;

C. Giá trị tuyệt đối của một số luôn là một số không dương.

D. Giá trị tuyệt đối của một số luôn là một số âm.

Xem đáp án

Đáp án đúng là: B.

Giá trị tuyệt đối của một số luôn là một số không âm: |x| ≥ 0 với mọi số thực x.

Câu 3:

Với mọi $x \in ℚ$ khẳng định nào sau đây là sai?

A. |x| = |–x|;

B. |x| < –x;

C. |x| ≥ 0;

D. |x| ≥ x.

Xem đáp án

Đáp án đúng là: B.

Với mọi $x \in ℚ$ ta luôn có |x| = |–x|; |x| ≥ 0 và |x| ≥ x nên B sai.

Với x 0 thì |x| = x > - x

Với x < 0 thì |x| = - x

Nên |x| - x

Câu 4:

Giá trị tuyệt đối của $- \frac{16}{6}$ là:

A. $- \frac{8}{3}$

B. $\frac{8}{3}$ ;

C. $- \frac{16}{6}$ ;

D. $\frac{6}{16}$

Xem đáp án

Đáp án đúng là: B.

Vì $- \frac{16}{6} < 0$ nên $|- \frac{16}{6}| = - (- \frac{16}{6}) = \frac{16}{6} = \frac{8}{3} .$

Vậy giá trị tuyệt đối của $- \frac{16}{6}$ là $\frac{8}{3}$

Câu 5:

Chọn khẳng định sai:

A. |–2,5| = 2,5;

B. |0| = 0;

C. |3,8| = ±3,8;

D. $|- \sqrt{7}| > 0$ .

Xem đáp án

Đáp án đúng là: C.

Vì –2,5 < 0 nên |–2,5| = –(–2,5) = 2,5. Do đó phương án A đúng.

Vì |0| = 0 nên phương án B đúng.

Vì 3,8 > 0 nên |3,8| = 3,8. Do đó phương án C sai.

Vì $- \sqrt{7} < 0$ nên $|- \sqrt{7}| = - (- \sqrt{7}) = \sqrt{7}$ >0. Do đó phương án D đúng.

Câu 6:

Chọn khẳng định đúng.

A. |–0,6| > |–0,7|;

B. |–0,6| = –0,6;

C. $|\sqrt{0, 7}| > |- \sqrt{0, 7}|;$

D. $|\frac{2}{3}| > |- \frac{1}{3}|$ .

Xem đáp án

Đáp án đúng là: D.

+) Ta có –0,6 < 0 nên |–0,6| = –(–0,6) = 0,6. Do đó phương án B sai.

Vì –0,7 < 0 nên |–0,7| = –(–0,7) = 0,7.

Vì 0,6 < 0,7 nên |–0,6| < |–0,7|. Do đó phương án A sai.

+) Vì $\sqrt{0, 7}$ và $- \sqrt{0, 7}$ là hai số đối nhau nên $|\sqrt{0, 7}| = |- \sqrt{0, 7}|$ . Do đó phương án C sai.

+) Vì $\frac{2}{3} > 0$ nên $|\frac{2}{3}| = \frac{2}{3}$ ;

Vì $- \frac{1}{3} < 0$ nên $|- \frac{1}{3}| = - (- \frac{1}{3}) = \frac{1}{3}$

Vì $\frac{2}{3} > \frac{1}{3}$ nên $|\frac{2}{3}| > |- \frac{1}{3}|$ . Do đó phương án D đúng.

Câu 7:

Trên trục số biểu diễn như sau:

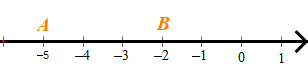
Độ dài đoạn thẳng AB là:

A. –3;

B. –7;

C. 3;

D. 7.

Xem đáp án

Đáp án đúng là: C.

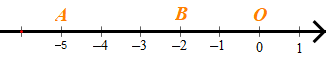
Trên trục số, điểm O biểu diễn gốc 0; điểm A biểu diễn số –5; điểm B biểu diễn số –2.

Khi đó OA = |–5| và OB = |–2|.

Ta có |–5| = –(–5) = 5; |–2| = –(–2) = 2.

Khi đó AB = OA – OB = 5 – 2 = 3.

Câu 8:

Tìm x biết |x| = $\frac{2}{3} .$

A. x = $\frac{2}{3};$

B. $x = - \frac{2}{3};$

C. $x = \frac{2}{3}$ hoặc $x = - \frac{2}{3};$

D. Không có giá trị x nào thoả mãn yêu cầu đề bài.

Xem đáp án

Đáp án đúng là: C.

Vì |x| = $\frac{2}{3}$ nên $x = \frac{2}{3}$ hoặc $x = - \frac{2}{3} .$

Vậy giá trị x thoả mãn $x = \frac{2}{3}$ hoặc $x = - \frac{2}{3} .$

Câu 9:

Tìm tất cả các giá trị x thoả mãn $|x| = |- \frac{1}{2}|$ .

A. $x = \frac{1}{2}$ ;

B. $x = - \frac{1}{2};$

C. $x = \frac{1}{2}$ hoặc $x = - \frac{1}{2}$ ;

D. Không có giá trị nào của x thoả mãn.

Xem đáp án

Đáp án đúng là: C.

Tìm tất cả các giá trị x thoả mãn |x| = |-1/2|. A. x = 1/2; B. x = -1/2; C. x = 1/2 (ảnh 1)

Câu 10:

Giá trị của biểu thức A = –|–3,6| : 1,2 là:

A. A = –3;

B. A = 3;

C. A = –0,3;

D. A = 0,3.

Xem đáp án

Đáp án đúng là: A.

A = –|–3,6| : 1,2

A = –[–(–3,6)] : 1,2

A = –[3,6] : 1,2

A = –3.

Vậy A = –3.

Câu 11:

Cho biểu thức M = |x + 3,4| – |–1,5|. Khi x = –0,2 thì giá trị của M là:

A. 4,7;

B. 1,7;

C. –4,7;

D. –1,7.

Xem đáp án

Đáp án đúng là: B.

Thay x = –0,2 vào biểu thức M = |x + 3,4| – |–1,5| ta được:

M = |–0,2 + 3,4| – |–1,5|

M = |3,2| – [–(–1,5)]

M = 3,2 – 1,5

M = 1,7.

Vậy khi x = –0,2 thì M = 1,7.

Câu 12:

Cho biểu thức N = |3x – 0,5| + $|- 1 \frac{3}{4}|$ . Khi x = –2 thì giá trị của N là:

A. $- \frac{33}{4};$

B. $\frac{27}{4};$

C. $\frac{33}{4};$

D. $\frac{59}{4} .$

Xem đáp án

Đáp án đúng là: C.

Thay x = –2 vào biểu thức N = |3x – 0,5| + $|- 1 \frac{3}{4}|$ ta được:

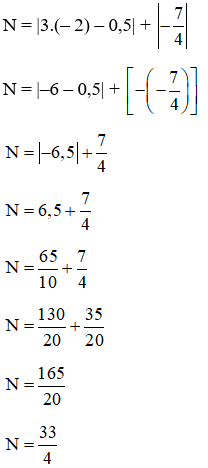
Cho biểu thức N = |3x – 0,5| + |-1 3/4|. Khi x = –2 thì giá trị của N là: (ảnh 1)

Câu 13:

Tìm số thực dương x biết $|x + \sqrt{2}| = 0$

A. x = 0;

A. $x = \sqrt{2};$

B. $x = - \sqrt{2};$

C. $x = - \sqrt{- 2}$ .

D. Không có số thực dương x nào thoả mãn.

Xem đáp án

Đáp án đúng là: D.

$|x + \sqrt{2}| = 0$

$x + \sqrt{2} = 0$

$x = - \sqrt{2}$

Mà x là số thực dương nên x > 0, do đó $x = - \sqrt{2}$ không thoả mãn.

Vậy không có số thực dương x nào thoả mãn.

Câu 14:

Tìm số thực x biết |x – 2021| = –2022.

A. x = 1;

B. x = –1;

C. x = 4043;

D. Không có số thực x nào thoả mãn.

Xem đáp án

Đáp án đúng là: D.

Vì |x – 2021| > 0 với mọi số thực x, mà –2022 < 0.

Vậy không có số thực x nào thoả mãn yêu cầu đề bài.

Câu 15:

Có bao nhiêu giá trị x thoả mãn 7,5 – 3.|5 – 2x| = –4,5?

A. 0;

B. 1;

C. 2;

D. 3.

Xem đáp án

Đáp án đúng là: C.

Ta có:

7,5 – 3.|5 – 2x| = –4,5

3.|5 – 2x| = 7,5 –(–4,5)

3.|5 – 2x| = 7,5 + 4,5

3.|5 – 2x| = 12

|5 – 2x| = 12 : 3

|5 – 2x| = 4

Trường hợp 1: 5 – 2x = 4

2x = 5 – 4

2x = 1

$x = \frac{1}{2}$

Trường hợp 2: 5 – 2x = –4

2x = 5 – (–4)

2x = 5 + 4

2x = 9

x = 9 : 2

$x = \frac{9}{2}$

Vậy có hai giá trị của x thoả mãn là $x = \frac{1}{2}$ ; $x = \frac{9}{2}$ .

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 7 Bài 3. Giá trị tuyệt đối của một số thực có đáp án

Trắc nghiệm Toán 7 Bài 3. Giá trị tuyệt đối của một số thực có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương