Dạng 3. Vẽ hai đường thẳng song song với điều kiện cho trước có đáp án
-
1027 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho đường thẳng y và điểm M nằm ngoài đường thẳng y như hình vẽ:
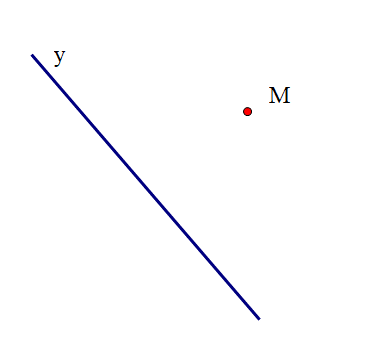
Vẽ đường thẳng x qua M và song song với đường thẳng y.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
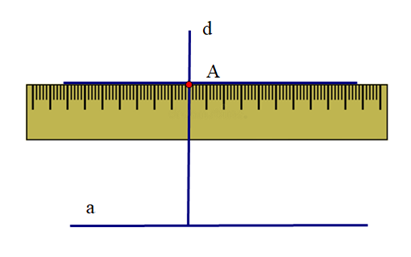
Để vẽ đường thẳng x qua M và song song với đường thẳng y, ta làm như sau:
+ Đặt thước kẻ sao cho chiều rộng của thước kẻ nằm trên đường thẳng y, chiều dài đi qua điểm M.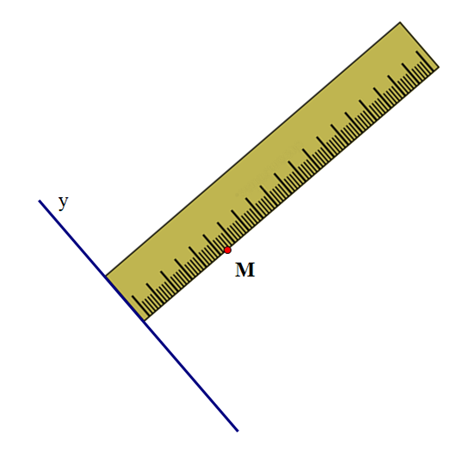
+ Vẽ theo cạnh đi qua điểm M của thước kẻ đường thẳng d
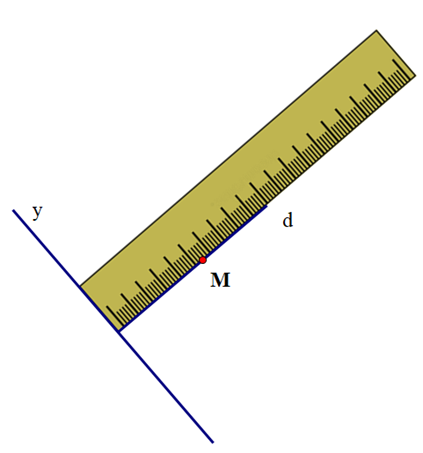
+ Đặt thước kẻ sao cho một vạch chia trên thước trùng với đường thẳng d và cạnh của thước đi qua điểm M
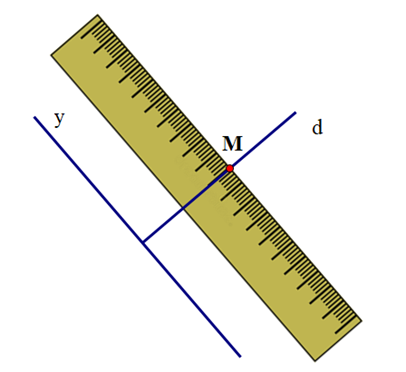
+ Vẽ theo cạnh đi qua điểm M của thước kẻ đường thẳng x
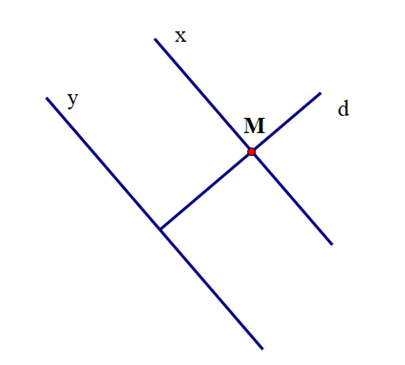
Câu 2:
Cho các hình vẽ sau:
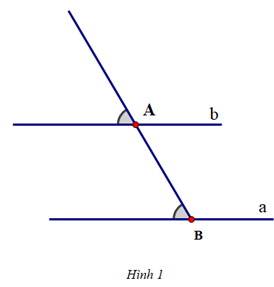
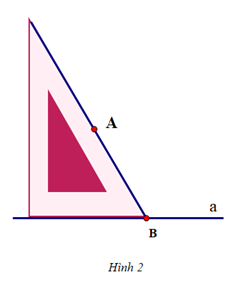
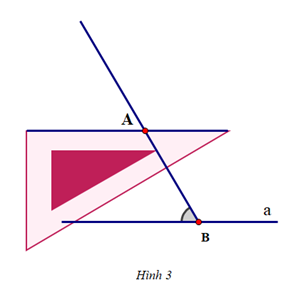
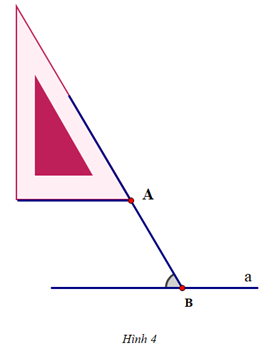
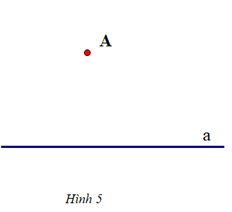
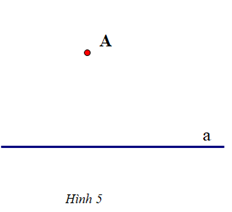
Để vẽ đường thẳng b đi qua A và song song với đường thẳng a cho trước, ta thực hiện theo thứ tự nào sau đây:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Để vẽ đường thẳng b đi qua A và song song với đường thẳng a cho trước, ta thực hiện theo thứ tự sau:
+ Cho đường thẳng a và một điểm A nằm ngoài đường thẳng a
+ Đặt ê ke sao cho cạnh góc vuông ngắn nằm trên đường thẳng a và cạnh huyền đi qua điểm A. Vẽ một đường thẳng theo cạnh huyền của ê ke
+ Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng đó còn cạnh góc vuông ngắn của ê ke đi qua điểm A. Vẽ theo cạnh góc vuông ngắn của ê ke một phần đường thẳng b
+ Hoàn thiện đường thẳng b
Vậy ta sắp xếp các hình vẽ trên theo thứ tự: Hình 5 – Hình 2 – Hình 4 – Hình 3 – Hình 1
Câu 3:
Để vẽ một đường thẳng d đi qua điểm M và song song với đường thẳng a cho trước, ta thực hiện hai bước như sau:
+ Bước 1: Vẽ đường thẳng c đi qua điểm M và vuông góc với đường thẳng a.
+ Bước 2: Vẽ đường thẳng d đi qua điểm M và vuông góc với đường thẳng c mới vẽ ở bước 1 ta được đường thẳng d song song với đường thẳng a.
Theo em, cách vẽ trên dựa vào tính chất nào sau đây?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
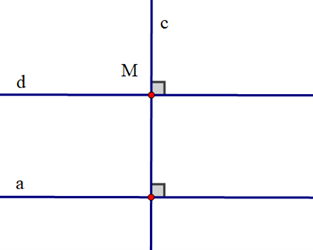
Vì hai đường thẳng a và d cùng vuông góc với đường thẳng c nên chúng song song với nhau. Do đó cách vẽ trên dựa vào tính chất: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Câu 4:
Cho đường thẳng a và một điểm M nằm ngoài đường thẳng a:

Khi đó, hình vẽ nào sau đây thể hiện đường thẳng b đi qua M và song song với a?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Cách vẽ ở hình C cho ta hai đường thẳng a và b song song với nhau vì đường thẳng c cắt hai đường thẳng a và b và tạo thành hai góc ở vị trí so le trong bằng nhau.
Câu 5:
Vì sao khi sử dụng ê ke (góc 60°) ta có thể vẽ được đường thẳng đi qua một điểm và song song với đường thẳng cho trước?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
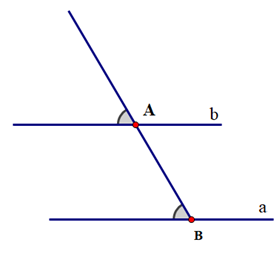
Khi vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước, ta có thể sử dụng ê ke (góc 60°) để vẽ vì nó sẽ tạo thành hai góc ở vị trí đồng vị bằng nhau (cùng bằng 60°) nên hai đường thẳng song song với nhau.
Câu 6:
Cho tam giác ABC:
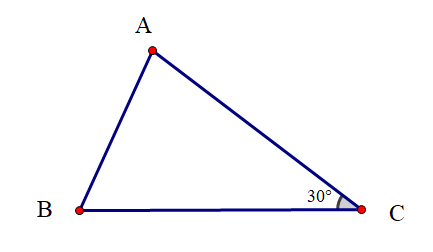
Vẽ đường thẳng m đi qua A và song song với BC?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Hình A cho thấy đường thẳng m đi qua A. Đồng thời m // AB vì có hai góc ở vị trí đồng vị đều bằng 30°.
Câu 7:
Cho hình vẽ sau:
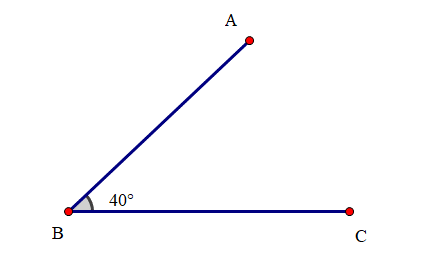
Vẽ đường thẳng d đi qua C và song song với AB?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Hình B cho thấy đường thẳng m đi qua C. Đường thẳng BC cắt hai đường thẳng AB, m và tạo thành hai góc ở vị trí trong cùng phía bù nhau nên AB và m song song với nhau.
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có thể vẽ một đường thẳng đi qua một điểm và song song với đường thẳng cho trước bằng: Thước kẻ, thước đo góc, ê ke.
Câu 9:
Cho hình vẽ sau:
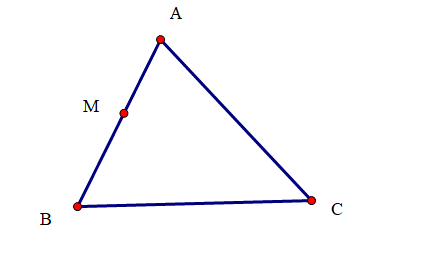
Vẽ đường thẳng MN song song với BC?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Hình A cho thấy đường thẳng MN đi qua M. Đường thẳng AC cắt hai đường thẳng BC, MN và tạo thành hai góc ở vị trí đồng vị bằng nhau nên MN song song với BC.
Câu 10:
Cho hình vẽ sau:
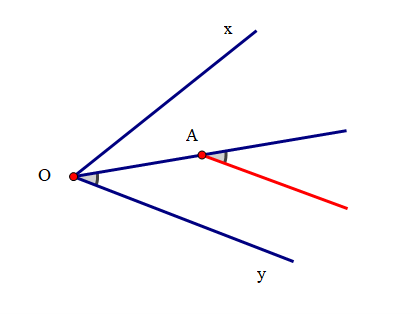
Vẽ đường thẳng đi qua A và song song với Ox?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Đường thẳng màu đỏ ở đáp án B đi qua A và song song với Ox.
Câu 11:
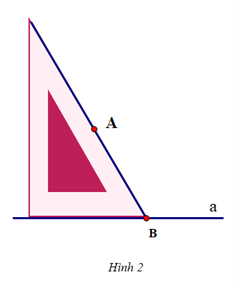
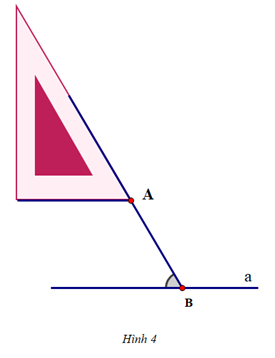
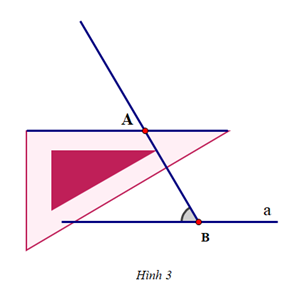
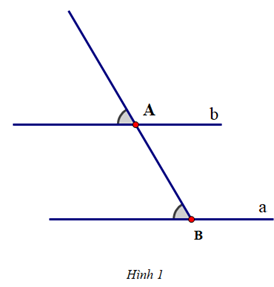
Cho ba hình vẽ sau:
Hình 1: 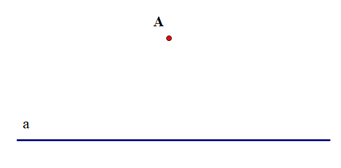
Hình 2: 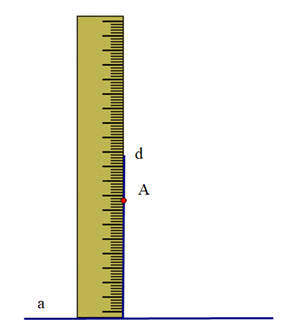
Hình 3: 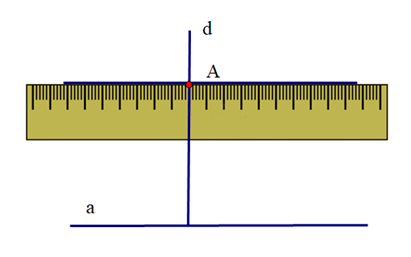
Sắp xếp các hình trên để được cách vẽ đường thẳng b đi qua A và song song với đường thẳng a:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Để vẽ đường thẳng b đi qua A và song song với đường thẳng a, ta thực hiện theo thứ tự:
Hình 1: 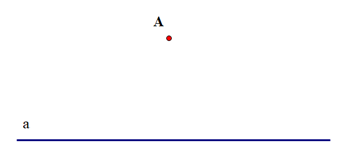
Hình 2: 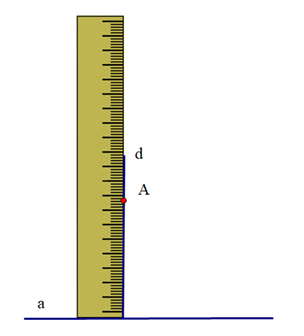
Hình 3: