Đề thi Học kì 1 Toán 7 Cánh diều có đáp án (Đề 2)
-
2056 lượt thi
-
17 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Cách viết – 0,5 ∈ ℚ là đúng vì – 0,5 = là số hữu tỉ.
Cách viết ∉ ℤ là đúng vì = – 1,5 không phải là số nguyên.
Cách viết –1 ∈ ℕ là sai vì –1 không phải là số tự nhiên.
Cách viết ∈ ℚ là đúng vì là số hữu tỉ.
Vậy ta chọn phương án C.
Câu 4:
Nhận định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
• Mọi số thập phân vô hạn không tuần hoàn là số thực, đây là khẳng định đúng.
• Mọi số thực đều là số vô tỉ, đây là khẳng định sai vì chẳng hạn số tự nhiên cũng là số thực nhưng không là số vô tỉ.
• Mọi số nguyên đều là số hữu tỉ, đây là khẳng định đúng vì mọi số nguyên a đều viết được dưới dạng , là số hữu tỉ.
• Số 0 là số hữu tỉ và cũng là số thực, đây là khẳng định đúng vì 0 = là số hữu tỉ, và cũng là số thực.
Vậy ta chọn phương án B.
Câu 5:
Khẳng đinh nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
• Giá trị của một số thực có thể là một số dương, một số âm hoặc số 0. Do đó A và B là khẳng định sai.
• Hai số đối nhau có giá trị tuyệt đối bằng nhau, đây là khẳng định đúng.
• Giá trị tuyệt đối của một số thực là số đối của nó, đây là khẳng định sai vì chỉ có giá trị tuyệt đối của một số âm mới là số đối của nó.
Vậy ta chọn phương án C.
Câu 6:
Dạng số thập phân vô hạn tuần hoàn của phân số là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có = –0,53333… = – 0,5(3).
Câu 7:
Nhận xét đúng về vị trí của các số thực 0; ; trên trục số là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: ![]()
Do đó trên trục số:

• Điểm nằm bên trái điểm . Do đó A đúng và B sai.
• Điểm nằm bên phải điểm 0. Do đó C sai.
• Điểm 0 nằm bên trái điểm . Do đó D sai.
Ta chọn phương án A.
Câu 8:
Tỉ lệ thức nào sau đây không được lập từ tỉ lệ thức ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Từ tỉ lệ thức , ta suy ra x . b = 2 . a.
Khi đó ta có các tỉ lệ thức sau:
⦁ . Suy ra phương án A đúng.
⦁ . Suy ra phương án C đúng.
⦁ . Suy ra phương án D đúng.
Do đó phương án B sai.
Vậy ta chọn phương án B.
Câu 9:
Phát biểu nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương án D sai vì hệ số tỉ lệ k ≠ 0.
Vậy ta chọn phương án D.
Câu 10:
Trong các hình khai triển dưới đây, có bao nhiêu hình gấp lại được thành một hình lăng trụ đứng?
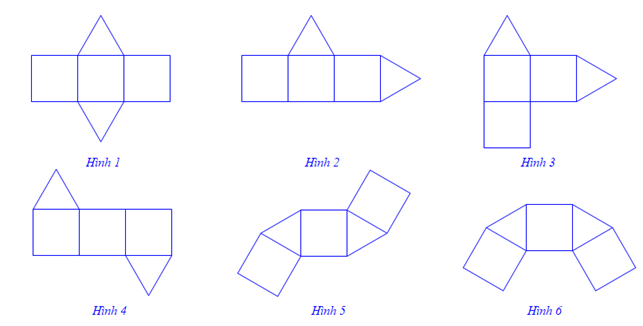
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trong các hình trên, Hình 1, Hình 4 và Hình 5 ghép lại được hình lăng trụ đứng tam giác.
Vậy có 3 hình.
Câu 11:
Cho hình vẽ sau:
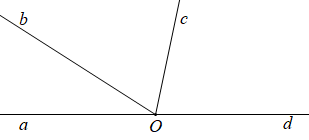
Số cặp góc kề bù (không kể góc không và góc bẹt) có trong hình vẽ trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Các cặp góc kề bù (không kể góc không và góc bẹt) có trong hình vẽ trên là: và ; và .
Vậy có 2 cặp góc kề bù với nhau.
Câu 12:
Cho ba điểm A, B, C. Qua điểm A vẽ đường thẳng a song song với đường thẳng BC. Qua điểm C vẽ đường thẳng b song song với đường thẳng AB. Hỏi vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
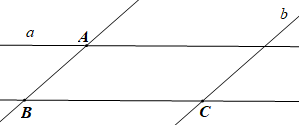
Theo Tiên đề Euclid:
• Qua điểm A chỉ vẽ được 1 đường thẳng a song song với đường thẳng BC;
• Qua điểm C chỉ vẽ được 1 đường thẳng b song song với đường thẳng AB.
Vậy ta chọn phương án A.
Câu 14:
Tìm x, biết:
a) (2x + 1)2 = 25;
b)
 Xem đáp án
Xem đáp án
a) (2x + 1)2 = 25
Trường hợp 1:
(2x + 1)2 = 25 = 52
2x + 1 = 5
2x = 4
x = 2.
Trường hợp 1:
(2x + 1)2 = 25 = (–5)2
2x + 1 = –5
2x = –6
x = –3.
Vậy x = 2 hoặc x = –3.
b) Từ tỉ lệ thức suy ra –3(2 – x) = 4(3x –1)
–3.2 –3.(–x) = 4.3x – 4.1
–6 + 3x = 12x – 4
3x – 12x = –4 + 6
–9x = 2
x = 2 : (–9)
Vậy .
Câu 15:
Trong dịp Tết vừa rồi, mẹ Hoa đã đi siêu thị Big C để mua bánh kẹo. Mẹ Hoa chọn ba loại bánh: bánh quy bơ Danisa giá 140 000 đồng 1 hộp, bánh Kitkat giá 80 000 đồng 1 hộp và bánh yến mạch giá 40 000 đồng một gói. Hỏi mẹ đã mua bao nhiêu hộp bánh Danisa biết số tiền mua mỗi loại bằng nhau và số hộp Kitkat ít hơn số gói yến mạch là 7 hộp?
 Xem đáp án
Xem đáp án
Gọi x, y, z (hộp) lần lượt là số hộp bánh Danisa, bánh Kitkat, bánh yến mạch mà mẹ Hoa đã mua.
Vì số hộp bánh Kitkat nhiều hơn bánh yến mạch 7 gói nên ta có z – y = 7.
Mẹ Hoa đã mua mỗi loại bánh với số tiền như nhau nên:
140 000x = 80 000y = 40 000z
Suy ra 14x = 8y = 4z
Do đó hay
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Khi đó:
• nên x = 4 (hộp);
• nên y = 7 (hộp);
• nên z = 14 (hộp).
Vậy số hộp bánh Danisa, bánh Kitkat, bánh yến mạch lần lượt là 4 hộp, 7 gói, 14 gói.
Câu 16:
Một nhóm thợ xây có 100 khối bê tông có dạng như hình dưới đây.
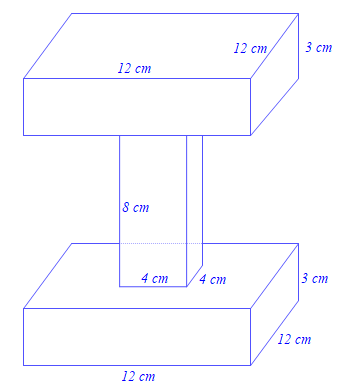
Người ta muốn sơn tất cả các mặt của từng khối bê tông. Hỏi số tiền sơn số bê tông đó là bao nhiêu đồng? Biết rằng số tiền để sơn 1 m2 bê tông là 100 000 đồng.
 Xem đáp án
Xem đáp án
Ta chia khối bê tông thành ba hình khối như hình vẽ dưới đây, trong đó hình (1) và hình (3) có diện tích tất cả các mặt bằng nhau.
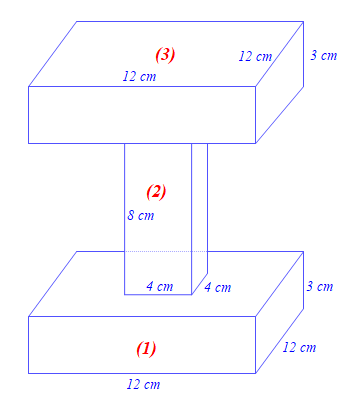
Diện tích xung quanh của hình hộp chữ nhật (1) là:
S1 = 2.(12 + 12).3 = 144 (cm2).
Diện tích một mặt đáy của hình hộp chữ nhật (1) là:
S2 = 12.12 = 144 (cm2).
Diện tích tiếp giáp giữa hình hộp chữ nhật (1) với hình hộp chữ nhật (2) chính là diện tích một mặt đáy của hình hộp chữ nhật (2) và bằng:
S3 = 4.4 = 16 (cm2).
Diện tích xung quanh của hình hộp chữ nhật (2) là:
S4 = 2.(4 + 4).8 = 128 (cm2).
Diện tích tiếp giáp giữa hình hộp chữ nhật (2) với hình hộp chữ nhật (3) bằng S3 = 16 (cm2).
Khi đó diện tích tất cả các mặt của khối bê tông là:
S = 2.[S1 + S2 + (S2 – S3)] + S4
= 2.[144 + 144 + (144 – 16)] + 128 = 960 (cm2) = 0,096 (m2).
Chi phí sơn một khối bê tông là: 0,096 . 100 000 = 9 600 (đồng)
Chi phí sơn 100 khối bê tông là: 9 600 . 100 = 960 000 (đồng).
Câu 17:
Cho hình vẽ dưới đây.
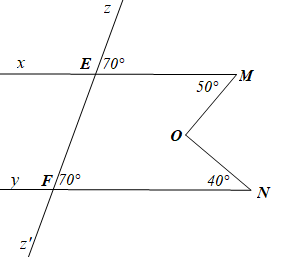
a) Vẽ lại hình và viết giả thiết kết luận.
b) Chứng minh Mx // Ny.
c) Tính số đo góc MON.
 Xem đáp án
Xem đáp án
Theo phương án 2 ta có: Số tiền nhận được vào ngày thứ nhất là 3 đồng; ngày thứ hai là 3 . 3 = 32 đồng; ngày thứ ba là 32 . 3 = 33 đồng; … ; ngày thứ mười bảy là 317 đồng.
Như vậy số tiền công nhận được theo phương án 2 là:
T = 3 + 32 + 33 + … + 317
Suy ra 3T = 3 . (3 + 32 + 33 + … + 317)
= 3. 3 + 3. 32 + 3 . 33 + … + 3 . 317
= 32 + 33 + 34 + … + 318
Do đó 3T – T = (32 + 33 + 34 + … + 318) – (3 + 32 + 33 + … + 317)
Hay 2T = 318 – 3 = 387 420 489 – 3 = 387 420 486 (đồng)
Suy ra T = 193 710 243 (đồng) > 170 000 000 (đồng).
Vậy nhóm kĩ thuật viên nên chọn phương án 2 để nhận được nhiều tiền công hơn.
