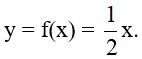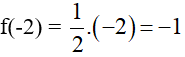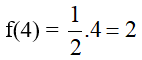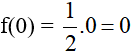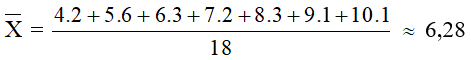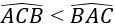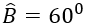Đề thi Toán lớp 7 Giữa kì 2 có đáp án (Đề 1)
-
1403 lượt thi
-
7 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Điền dấu “Đ, S” vào chỗ trống (…) một cách thích hợp.
1. -0.35 là một đơn thức (…)
2. Bậc của là 5 (…)
3. là đa thức bậc 2 (…)
4. Cho A = 3x + y và B = x – 3y thì A + B = 2x + 2y (…)
Xem đáp án
1. -0.35 là một đơn thức (Đ)
2. Bậc của là 5 (S)
3. là đa thức bậc 2 (Đ)
4. Cho A = 3x + y và B = x – 3y thì A + B = 2x + 2y (S)
Câu 2:
Điền dấu “Đ, S” vào chỗ trống (…) một cách thích hợp.
1. Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn (…)
2. Tam giác có cân có 1 góc bằng 600 là tam giác đều (…)
3. Ba đoạn thẳng 5cm, 3cm, 9cm có thể là 3 cạnh của tam giác (…)
4. Nếu ba góc của tam giác này bằng ba góc của tam giác kia thì 2 tam giác đó bằng nhau (…)
5. Trong tam giác ABC thì |BC - AB| < AC < BC + AC (…)
6. Trong tam giác ABC cân tại B, AC= 5cm, AB= 3cm thì chu vi tam giác là 13cm (…)
Xem đáp án
1. Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn (Đ)
2. Tam giác có cân có 1 góc bằng 600 là tam giác đều (Đ)
3. Ba đoạn thẳng 5cm, 3cm, 9cm có thể là 3 cạnh của tam giác (S)
4. Nếu ba góc của tam giác này bằng ba góc của tam giác kia thì 2 tam giác đó bằng nhau (S)
5. Trong tam giác ABC thì |BC - AB| < AC < BC + AC (Đ)
6. Trong tam giác ABC cân tại B, AC= 5cm, AB= 3cm thì chu vi tam giác là 13cm (S)
Câu 3:
Cho hàm số y = f(x) = ax, biết đồ thị của hàm số đi qua điểm A(2; 1).
a) Hãy xác định hệ số a.
b) Tính f(-2); f(4); f(0).
Xem đáp án
a) Đồ thị hàm số y = ax đi qua điểm A(2; 1) nên ta có: 1 = 2.a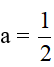 
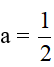
. Vậy thì đồ thị hàm số đi qua điểm A(2;1).
b) Với 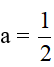thì 
Ta có: 
Câu 4:
Thời gian làm một bài tập Toán của một số học sinh lớp 7 (tính bằng phút) được thống kê bởi bảng sau:
| 5 5 6 | 6 8 5 | 7 8 5 | 4 8 5 | 5 9 4 | 6 7 10 |
a) Dấu hiệu ở đây là gì ? Số các giá trị là bao nhiêu?
b) Lập bảng tần số. Tính số trung bình cộng?
c) Tìm Mốt của dấu hiệu?
Xem đáp án
a) Dấu hiệu: Thời gian làm một bài tập Toán của mỗi học sinh lớp 7 (tính theo phút)
Số các giá trị là: 18
b) Lập bảng tần số.
| Giá trị | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Tần số | 2 | 6 | 3 | 2 | 3 | 1 | 1 | N = 18 |
Số trung bình cộng: 
c) Mốt của dấu hiệu là 5.
Câu 6:
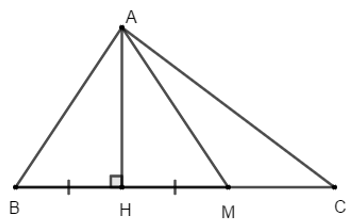
Cho tam giác ABC có ; AB= 7cm; BC= 15 cm. Vẽ AH vuông góc với BC (H thuộc BC). Lấy điểm M trên HC sao HM= HB.
a) So sánh góc BAC và ACB.
b) Chứng minh tam giác ABM đều.
c) Tam giác ABC có phải là tam giác vuông không? Vì sao?
Xem đáp án
Chứng minh
a) Trong tam giác ABC có: AB = 7 cm; BC = 15 cm nên AB < BC
Do đó: 
b) Xét tam giác ABH và tam giác AMH cùng vuông tại H có:
AH: cạnh chung
HB = HM (gt)
Do đó: (hai cạng góc vuông)
Suy ra: AB = AM (hai cạnh tương ứng)
Nên ABM cân tại A
Mà 
Do đó tam giác ABM đều.
c) Ta có: BM = AB = 7 cm ( tam giác ABM đều)
Suy ra BH = HM = 7/2 = 3,5 cm
HC = BC - BH = 15 - 3,5 = 11,5 cm
Áp dụng định lý Pytago trong tam giác ABH vuông tại H:
Áp dụng định lý Pytago trong tam giác ACH vuông tại H:
AC = 13 cm
Vì nên
Vậy tam giác ABC không phải là tam giác vuông.
