Giải SBT Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết có đáp án
Giải SBT Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết có đáp án
-
257 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
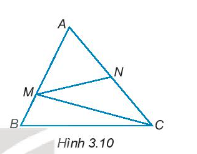
Cho Hình 3.10.
a) Viết tên góc so le trong với góc NMC.
b) Viết tên góc đồng vị với góc ACB, góc AMN.
Xem đáp án
Lời giải:
a) Góc so le trong với góc NMC là góc MCB.
b) Góc đồng vị với góc ACB là góc ANM;
Góc đồng vị với góc AMN là góc ABC.
Câu 2:
Vẽ đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng a đi qua M và song song với d.
Xem đáp án
Lời giải:
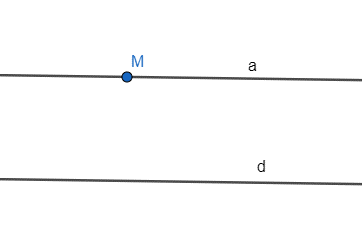
Câu 3:
Xem đáp án
Lời giải:
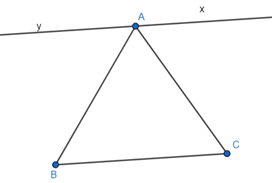
Câu 4:
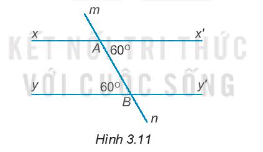
Xem đáp án
Lời giải:
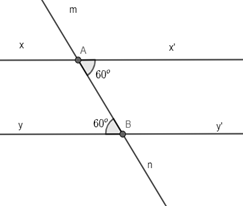
Ta có: Góc x’An và góc mBy là hai góc so le trong
Mặt khác \(\widehat {x'An} = \widehat {mBy} = 60^\circ \)
Do đó, hai đường thẳng xx’ và yy’ song song với nhau.
Câu 5:
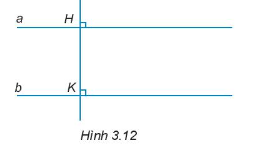
Xem đáp án
Lời giải:
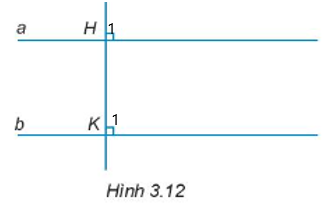
Vì HK vuông góc với a nên \(\widehat {{H_1}} = 90^\circ \);
Vì HK vuông góc với b nên \(\widehat {{K_1}} = 90^\circ \).
Mà \(\widehat {{H_1}};\widehat {{K_1}}\) là hai góc đồng vị.
Do đó, a // b.
Câu 6:
Xem đáp án
Lời giải:
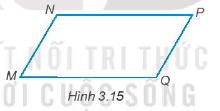
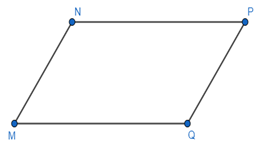
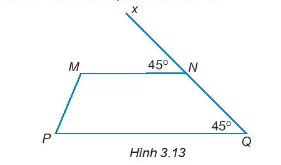
Đường thẳng QN cắt đường thẳng MN và PQ lần lượt tại N và Q.
Từ hình vẽ ta thấy: \(\widehat {xNM} = 45^\circ \); \[\widehat {NQP} = 45^\circ \]
Mà hai góc này ở vị trí đồng vị.
Do đó MN // PQ.
Câu 7:
Xem đáp án
Lời giải:
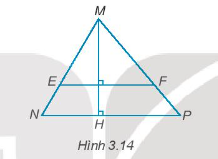
Từ hình vẽ ta thấy:
MH vuông góc với NP; MH vuông góc với EF nên EF // NP (quan hệ từ vuông góc đến song song).
Câu 9:
Xem đáp án
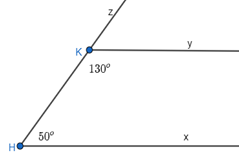
Vì góc \(\widehat {zKy}\) và góc \(\widehat {yKH}\) là hai góc kề bù.
Do đó, \(\widehat {zKy}\) + \(\widehat {yKH}\) = 180o
Thay số: \(\widehat {zKy}\) + 130o = 180o
\(\widehat {zKy}\) = 180o – 130o
\(\widehat {zKy}\) = 50o.
Vì \(\widehat {zKy}\) và \(\widehat {zKy}\) là hai góc đồng vị và \(\widehat {zKy}\) = \(\widehat {zKy}\) = 50o.
Do đó, Ky // Hx.