Giải VTH Toán 7 CTST Bài 4. Bài tập cuối chương 9 có đáp án
-
176 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Sử dụng các dữ kiện sau để trả lời các câu hỏi B1 – B3.
Gieo đồng thời hai con xúc xắc 6 mặt cân đối, đồng chất và khác màu. Xét biến cố sau:
E: “ Hai xúc xắc xuất hiện trên mặt có số chấm bằng nhau”.
F: “ Tổng số chấm xuất hiện trên hai xúc xắc lớn hơn 1”.
G: “ Hiệu số chấm xuất hiện trên hai xúc xắc bằng 6”.
H: “ Tổng số chấm xuất hiện trên 2 xúc xắc bằng 7.”
Có bao nhiêu biến cố chắc chắn trong các biến cố trên?
A. 0;
B. 1;
C. 2;
D. 3.
Xem đáp án
Lời giải
Biến cố E là biến cố ngẫu nhiên do hai xúc xắc có thể xuất hiện mặt có số chấm bằng nhau hoặc không, ta không thể biết trước được biến cố có xảy ra hay không.
Biến cố F là biến cố chắc chắn do tổng số chấm xuất hiện trên hai xúc xắc luôn lớn hơn 1 ( nhỏ nhất bằng 2).
Biến cố G là biến cố không thể do hiệu số chấm xuất hiện trên hai xúc xắc luôn nhỏ hơn 6 ( nhỏ nhất bằng 5).
Biến cố H là biến cố ngẫu nhiên do tổng số chấm xuất hiện trên hai xúc xắc có thể bằng 7 hoặc khác 7, ta không thể biết trước là nó có xảy ra hay không.
Vậy có 1 biến cố chắc chắn. Chọn đáp án B.
Câu 2:
Có bao nhiêu biến cố ngẫu nhiên trong các biến cố trên?
A. 0;
B. 1;
C. 2;
D. 3.
Xem đáp án
Lời giải
Biến cố E là biến cố ngẫu nhiên do hai xúc xắc có thể xuất hiện mặt có số chấm bằng nhau hoặc không, ta không thể biết trước được biến cố có xảy ra hay không.
Biến cố F là biến cố chắc chắn do tổng số chấm xuất hiện trên hai xúc xắc luôn lớn hơn 1 ( nhỏ nhất bằng 2).
Biến cố G là biến cố không thể do hiệu số chấm xuất hiện trên hai xúc xắc luôn nhỏ hơn 6 ( nhỏ nhất bằng 5).
Biến cố H là biến cố ngẫu nhiên do tổng số chấm xuất hiện trên hai xúc xắc có thể bằng 7 hoặc khác 7, ta không thể biết trước là nó có xảy ra hay không.
Vậy có 2 biến cố ngẫu nhiên. Chọn đáp án C.
Câu 3:
Hai biến cố nào đồng khả năng?
A. E và F;
B. F và G;
C. G và H;
D. E và H.
Xem đáp án
Lời giải
Biến cố E có 6 khả năng xảy ra, khi 2 xúc xắc xuất hiện mặt có các cặp số: 1 và 1; 2 và 2; 3 và 3; 4 và 4; 5 và 5; 6 và 6.
Biến cố F là biến cố chắc chắn nên có khả năng xảy ra cao hơn biến cố E, G, H.
Biến cố G là biến cố không thể, có 0 khả năng xảy ra.
Biến cố H có 6 khả năng xảy ra, khi 2 xúc xắc xuất hiện mặt có các cặp số: 1 và 6; 2 và 5; 3 và 4; 4 và 3; 5 và 2; 6 và 1.
Vậy biến cố E và H có đồng khả năng xảy ra. Đáp án đúng là D.
Câu 4:
Sử dụng dữ kiện sau để trả lời các câu hỏi B4 – B6.
Chọn ngẫu nhiên một chữ cái trong từ MILLION. Xét các biến cố sau:
E: “ Chọn được chữ I.”; F: “ Chọn được chữ M.”;
G: “ Chọn được chữ L.”; H: “ Chọn được một phụ âm.”.
Biến cố nào có khả năng xảy ra cao nhất?
A. E;
B. F;
C. G;
D. H.
Xem đáp án
Lời giải
Trong từ MILLION có 2 chữ I; 1 chữ M; 2 chữ L và 4 phụ âm (M, L, L, N).
Vậy biến cố H có khả năng xảy ra cao nhất. Chọn đáp án D.
Câu 5:
Trong các biến cố trên, hai biến cố nào là đồng khả năng?
A. E và F;
B. E và G;
C. F và G;
D. G và H.
Xem đáp án
Lời giải
Trong từ MILLION có 2 chữ I; 1 chữ M; 2 chữ L và 4 phụ âm (M, L, L, N).
Biến cố chọn được 1 chữ I và biến cố chọn được 1 chữ L có đồng khả năng xảy ra. Hay biến cố E và G có đồng khả năng xảy ra.
Chọn đáp án B.
Câu 6:
Biến cố F có xác suất bằng:
A. 0;
B. \(\frac{1}{6}\);
C. \(\frac{1}{7}\);
D. 1.
Xem đáp án
Lời giải
Từ MILLION có 7 chữ cái nên mỗi chữ cái có khả năng lựa chọn như nhau. Do đó xác suất của biến cố F là \(\frac{1}{7}\).
Vậy chọn đáp án C.
Câu 7:
Tung một đồng xu 2 lần thấy có mặt ngửa xuất hiện. Trong các biến cố sau, những biến cố nào có thể xảy ra?
A: “ Cả hai lần tung có cùng mặt xuất hiện.”
B: “ Mặt ngửa xuất hiện ở lần tung đầu tiên.”
C: “ Mặt sấp xuất hiện ở cả hai lần tung.”
Xem đáp án
Lời giải
Biến cố A có thể xảy ra. Cả hai lần tung đều thấy mặt ngửa.
Biến cố B có thể xảy ra. Mặt ngửa có thể xuất hiện ở lần tung đầu tiên.
Biến cố C không thể xảy ra do đồng xu được tung có mặt ngửa xuất hiện. Mặt sấp chỉ có thể xuất hiện 1 lần hoặc không xuất hiện.
Câu 8:
Quay vòng quay như hình bên một lần. Xét hai biến cố sau:
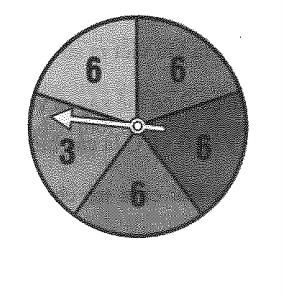
A: “ Mũi tên chỉ vào ô ghi số 3.”
B: “ Mũi tên chỉ vào ô ghi số 6.”
a) Trong hai biến cố A và B, biến cố nào có khả năng xảy ra cao hơn?
b) Tính xác suất của biến cố A. Để biến cố B có xác suất bằng 1 thì các số ghi trên vòng quay cần có thay đổi gì?
Xem đáp án
Lời giải
a) Biến cố B có khả năng xảy ra cao hơn vì vòng quay có 1 ô số 3 và 4 ô số 6.
b) Xác suất của biến cố A bằng \(\frac{1}{5}\).
Giải thích thêm: Khả năng quay vào các ô là như nhau nên có 5 ô và có 1 ô số 3 nên xác suất của biến cố A là \(\frac{1}{5}\).
Để biến cố B có xác suất bằng 1 thì vòng quay phải thay số 6 vào ô ghi số 3.
Câu 9:
Tàu du lịch trong khu vui chơi có 4 toa, mỗi toa chở tối đa 4 người. Có 14 em nhỏ vào chơi, chọn ngẫu nhiên tất cả các toa tàu để lên. Xét các biến cố:
E: “ Toa 1 có ít người nhất.”
F: “ Toa ít nhất cũng có 2 người.”
G: “ Số người trên 4 toa khác nhau.”
H: “ Có ít nhất 2 toa 4 người.”
a) Những biến cố nào là biến cố chắc chắn trong các biến cố trên?
b) Tính xác suất của biến cố G.
Xem đáp án
Lời giải
a)
- Nếu toa 1 có ít người nhất thì có thể có các trường hợp sau xảy ra:
TH1: Nếu toa 1 có 1 người thì 13 người còn lại xếp vào 3 toa, mỗi toa xếp tối đa 4 người thì có thể xếp được 12 người. Do đó TH này không thể xảy ra.
TH2: Nếu toa 1 có 2 người thì còn 12 người còn lại xếp vào 3 toa.
TH3: Nếu toa 1 có 3 hoặc 4 người thì chắc chắn sẽ có toa ít người hơn toa 1.
Vì vậy biến cố E là biến cố ngẫu nhiên.
- Nếu toa ít nhất có 1 người hoặc không có người nào, số người còn lại sẽ lớn hơn 12 người nên không thể chia vào 3 toa mỗi toa tối đa 4 người. Như vậy F là biến cố chắc chắn.
- Nếu số người trên 4 toa khác nhau, tức là 1 toa có 4 người, 1 toa có 3 người, 1 toa có 2 người, 1 toa có 1 người. Tổng số người trên tàu là 10 người, còn 4 người nữa chưa được lên. Như vậy biến cố G là biến cố không thể.
- Nếu xếp mỗi toa 3 người thì mới có 12 người được lên tàu. Như vậy còn 2 người xếp vào 2 toa bất kì. Suy ra có ít nhất 2 toa 4 người. Biến cố H là biến cố chắc chắn.
b) Biến cố G là biến cố không thể nên G có xác suất bằng 0.
Câu 10:
Viết ngẫu nhiên một số nguyên dương không lớn hơn 100. Xét các biến cố:
A: “Số vừa viết là bội chung nhỏ nhất của 12 và 15”
B: “Số vừa viết chia hết cho 4”.
C: “Số vừa viết là số nguyên tố”.
a) Tính xác suất của biến cố A;
Xem đáp án
Lời giải
a) A xảy ra khi viết ra số 60. Vậy xác suất của biến cố A bằng \(\frac{1}{{100}}\). (100 là số số nguyên dương không lớn hơn 100).
Câu 11:
Xem đáp án
Lời giải
b) Các số nguyên dương nhỏ hơn 100 chia hết cho 4 là: 4; 8; 12; 16; 20; 24; 28; 32; 36; 40; ...; 96; 100. Có tất cả 25 số.
Các số nguyên tố nhỏ hơn 100 là: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. Có tất cả 25 số.
Biến có B có thể xảy ra với 25 khả năng. Biến cố C có thể xảy ra với 25 khả năng. Vậy B và C là các biến cố đồng khả năng.
Câu 12:
Bạn Hải chơi trò chơi “Vòng quay tính điểm”. Mỗi lần quay, kim chỉ vào ô nào thì Hải sẽ nhận được số điểm bằng số ghi trên ô đó (hình bên). Xét các biến cố:
E: “ Kim chỉ ô ghi số 1000.”; F: “ Kim chỉ ô ghi số 750.” ;
G: “ Kim chỉ ô ghi số 500.” ; H: “ Kim chỉ ô ghi số 250.” .
a) Tính xác suất của biến cố E.
Xem đáp án
Lời giải
a) Kim có thể chỉ vào 10 ô trên vòng quay. Vậy xác suất của biến cố E bằng \(\frac{1}{{10}}\).
Câu 13:
Xem đáp án
Lời giải
b) Biến cố G có thể xảy ra với 2 khả năng; biến cố F có thể xảy ra với 3 khả năng; biến cố H có thể xảy ra với 4 khả năng. Vậy H là biến cố có khả năng xảy ra cao nhất.
Câu 14:
Một tòa nhà chung cư 25 tầng được đánh số lần lượt từ 1 đến 25. Bạn Sơn vào thang máy ở tầng 1, bấm ngẫu nhiên số của một tầng để đi lên tầng trên.
a) Tính xác suất Sơn lên đến tầng cao nhất của tòa nhà.
Xem đáp án
Lời giải
a) Sơn đi lên tầng cao nhất của tòa nhà, tức tầng 25. Biến cố này có xác suất bằng \(\frac{1}{{25}}\).
Câu 15:
b) Hai biến cố sau có đồng khả năng không?
B: “ Sơn đi lên tầng có số là một số chính phương.”
C: “ Sơn đi lên một trong các tầng nằm trên tầng 15.”
Xem đáp án
Lời giải
b) Biến cố B xảy ra khi Sơn lên tầng số 1, 4, 9, 16, 25.
Biến cố C xảy ra khi Sơn lên tầng số 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
Vậy biến cố B và C không đồng khả năng.
Câu 16:
Một xạ thủ cần tiêu diệt một mục tiêu. Khi có 3 viên đạn trúng liên tiếp, mục tiêu sẽ bị diệt và xạ thủ ngừng bắn. Quan sát thấy xạ thủ phải bắn hết 6 viên đạn mới tiêu diệt được mục tiêu. Xét các biến cố sau:
E: “ Ba viên đạn đầu tiên đều trượt mục tiêu.”
F: “ Viên đạn thứ hai và thứ 3 đều trúng mục tiêu.”
G: “ Viên đạn thứ 3 bắn trượt.”
a) Biến cố E có là biến cố ngẫu nhiên không?
Xem đáp án
Lời giải
a) Khi có 3 viên đạn trúng liên tiếp, mục tiêu mới bị diệt. Xạ thủ bắn hết 6 viên đạn mục tiêu mới bị diệt, nên viên đạn thứ 4, 5, 6 là 3 viên đạn liên tiếp bắn trúng mục tiêu.
Biến cố E là biến cố ngẫu nhiên do 3 viên đạn đầu tiên có thể đều trượt mục tiêu, hoặc có 1 viên trúng, hoặc nhiều nhất có 2 viên trúng, ta không biết trước được biến cố có xảy ra hay không.
Câu 17:
Xem đáp án
Lời giải
b) - Nếu viên đạn thứ 2 và thứ 3 đều trúng mục tiêu, ta có 3 viên 2, 3, 4 liên tiếp trúng mục tiêu và mục tiêu bị diệt ở viên đạn thứ 4, không đúng với đề bài là phải bắn hết 6 viên đạt. Nên F là biến cố không thể.
F là biến cố không thể nên F có xác suất bằng 0.
- Viên đạn thứ 3 luôn trượt vì để xạ thủ ngừng bắn ở viên thứ 6 thì ba viên đạn liên tiếp bắn trúng phải là viên thứ 4, 5, 6.
G là biến cố chắc chắn nên G có xác suất bằng 1.