Trắc nghiệm Toán 7 CTST Bài 3. Tam giác cân có đáp án (Phần 2) (Vận dụng)
-
606 lượt thi
-
3 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho ∆ABC cân tại A có CM là tia phân giác của \(\widehat {{\rm{ACB}}}\) và \(\widehat {\rm{A}} = 3\widehat {\rm{B}}\). Số đo của \(\widehat {{\rm{AMC}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
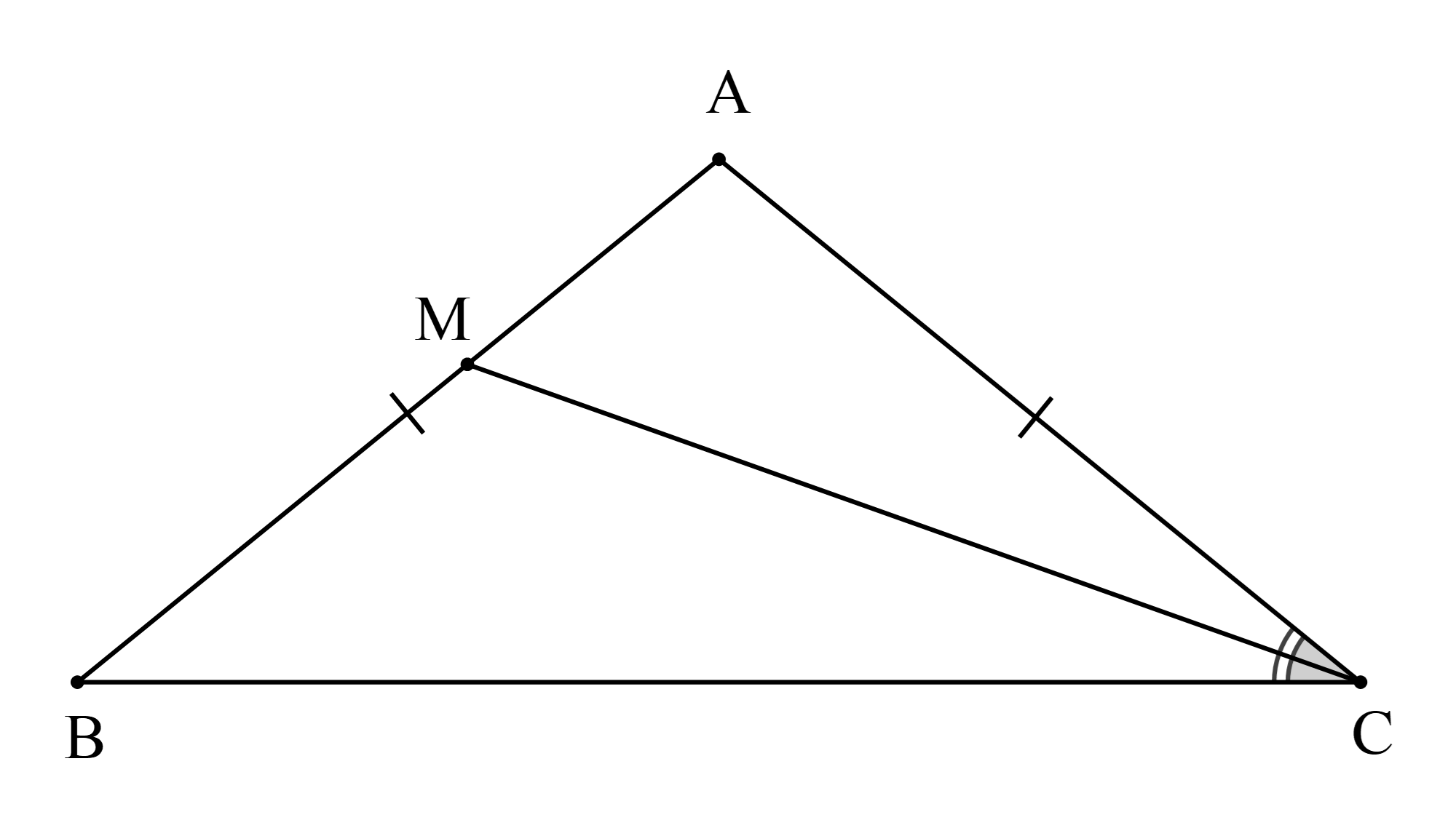
Theo bài ta có ∆ABC cân tại A nên \(\widehat {\rm{B}} = \widehat {{\rm{ACB}}}\) (tính chất tam giác cân)
Xét ∆ABC có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {{\rm{ACB}}} = 180^\circ \)(tổng ba góc trong tam giác bằng 180°) (1)
Mà \(\widehat {\rm{A}} = 3\widehat {\rm{B}}\) và \(\widehat {\rm{B}} = \widehat {{\rm{ACB}}}\)
Nên \(3\widehat {\rm{B}} + \widehat {\rm{B}} + \widehat {\rm{B}} = 180^\circ \)
Hay \(5\widehat {\rm{B}} = 180^\circ \)
Do đó \(\widehat {\rm{B}} = \frac{{180^\circ }}{5} = 36^\circ \)
Suy ra \(\widehat {\rm{B}} = \widehat {{\rm{ACB}}} = 36^\circ \); \(\widehat {\rm{A}} = 3\widehat {\rm{B}} = 3.36^\circ = 108^\circ \).
Ta lại có CM là tia phân giác của \(\widehat {{\rm{ACB}}}\)
Suy ra \(\widehat {{\rm{ACM}}} = \widehat {{\rm{CMB}}} = \frac{{\widehat {{\rm{ACB}}}}}{2} = \frac{{36^\circ }}{2} = 18^\circ \)
Xét ∆AMC có: \(\widehat {\rm{A}} + \widehat {{\rm{ACM}}} + \widehat {{\rm{AMC}}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(108^\circ + 18^\circ + \widehat {{\rm{AMC}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{AMC}}} = 180^\circ - 108^\circ - 18^\circ = 54^\circ \).
Vậy ta chọn phương án A.
Câu 2:
Cho hình vẽ
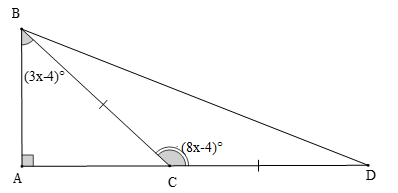
Số đo \(\widehat {{\rm{ABD}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì ∆ABC vuông tại A suy ra \(\widehat {{\rm{ABC}}} + \widehat {{\rm{ACB}}} = 90^\circ \) (tổng hai góc nhọn trong tam giác vuông bằng 90°).
Hay \(\widehat {{\rm{ACB}}} = 90^\circ - \widehat {{\rm{ABC}}} = 90^\circ - \left( {3x - 4} \right)^\circ = \left( {94 - 3x} \right)^\circ \).
Ta có \(\widehat {{\rm{ACB}}} + \widehat {{\rm{BCD}}} = 180^\circ \) (hai góc kề bù)
Hay \(\left( {94 - 3x} \right)^\circ + \left( {8x - 4} \right)^\circ = 180^\circ \)
Suy ra \[\left( {94 - 3x + 8x - 4} \right)^\circ = 180^\circ \]
Do đó 5x + 90 = 180
5x = 90
x = 18
Do đó \(\widehat {{\rm{BCD}}} = \left( {8.18 - 4} \right)^\circ = 140^\circ \).
Xét ∆BCD có CB = CD nên ∆BCD cân tại C.
Suy ra \(\widehat {{\rm{CBD}}} = \widehat {\rm{D}}\) (tính chất tam giác cân) (1)
Xét ∆BCD có \(\widehat {{\rm{BCD}}} + \widehat {{\rm{CBD}}} + \widehat {\rm{D}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Suy ra \(\widehat {{\rm{CBD}}} + \widehat {\rm{D}} = 180^\circ - \widehat {{\rm{BCD}}} = 180^\circ - 140^\circ = 40^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{CBD}}} = \widehat {\rm{D}} = \frac{{40^\circ }}{2} = 20^\circ \).
Vì ∆ABD vuông tại A suy ra \(\widehat {{\rm{ABD}}} + \widehat {\rm{D}} = 90^\circ \)
Suy ra \(\widehat {{\rm{ABD}}} = 90^\circ - 20^\circ = 70^\circ \).
Vậy ta chọn phương án B.
Câu 3:
Cho hình vẽ, biết rằng BC = 10 cm; AD = 16 cm và chu vi ∆ABC bằng 24 cm.
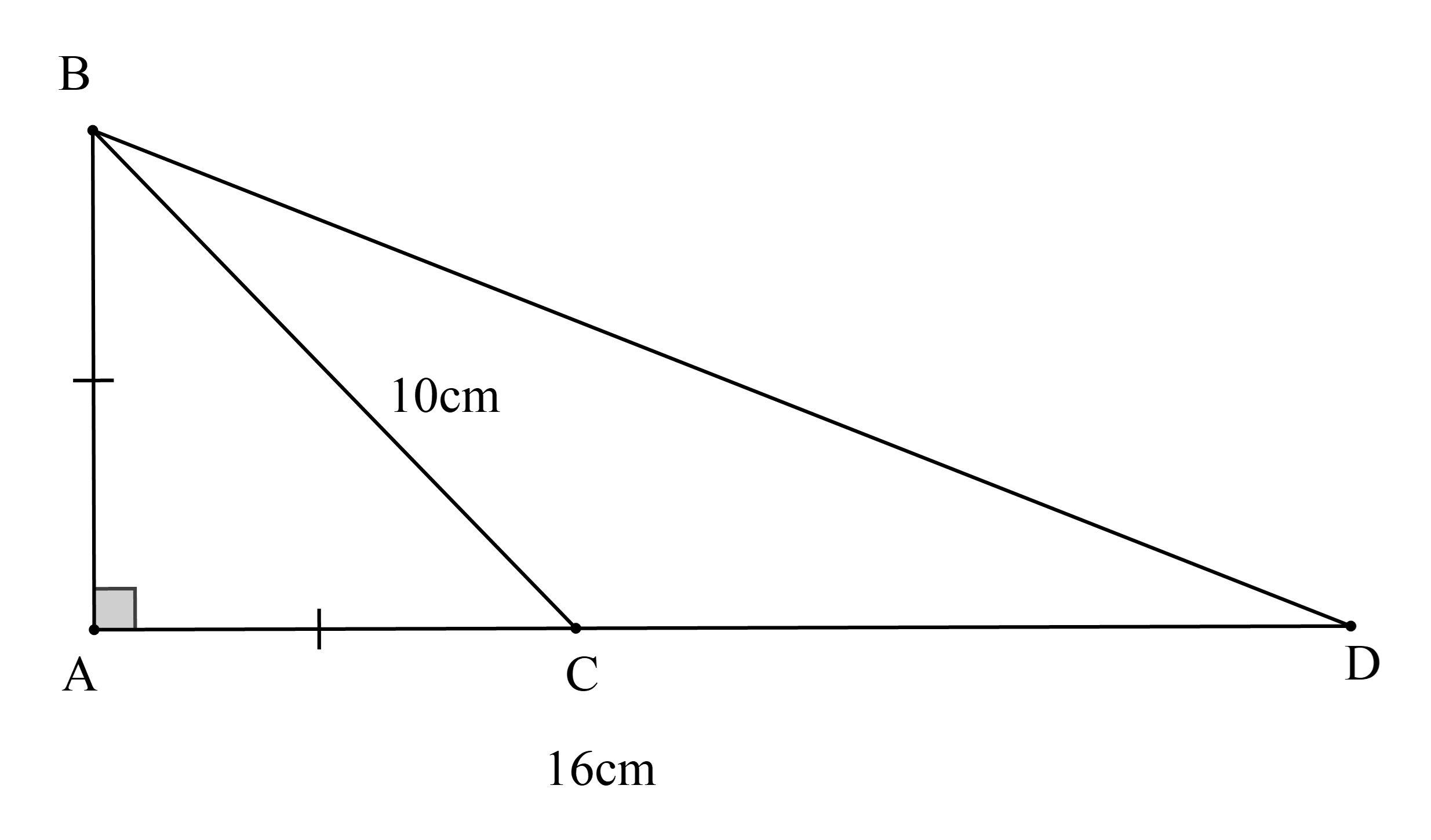
Diện tích ∆BCD là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì chu vi ∆ABC bằng 24 cm nên AB + AC + BC = 24 (cm).
Hay AB + AC = 24 – BC = 24 – 10 = 14 cm (1)
Mà AB = AC (2)
Từ (1) và (2) suy ra AB = AC = \(\frac{{14}}{2} = 7\) (cm).
Mặt khác AD = AC + CD
Hay 16 = 7 + CD nên CD = 9 (cm).
Diện tích tam giác BCD là: \({S_{BCD}} = \frac{1}{2}BA.CD = \frac{1}{2}.7.9 = 31,5\) (cm2).
Vậy ta chọn phương án B.
