Trắc nghiệm Toán 7 KNTT Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
Dạng 1. Vận dụng tiên đề Euclid về hai đường thẳng song song và chứng minh ba điểm thẳng hàng có đáp án
-
670 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
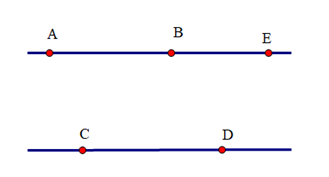
Cho AB // CD. Trên tia đối của tia BA lấy điểm E. Chứng minh BE // CD.
Xem đáp án
Hướng dẫn giải:
Ta có hai đường thẳng AB và CD song song với nhau.
Mà E nằm trên tia đối của tia BA.
Theo tiên đề Euclid ta có: Qua B chỉ kẻ được duy nhất một đường thẳng song song với CD.
Suy ra BE song song với CD.
Câu 2:
Xem đáp án
Hướng dẫn giải:
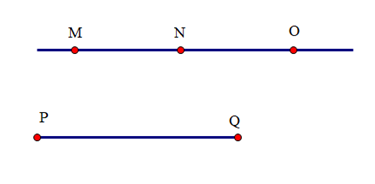
Theo tiên đề Euclid: chỉ có một đường thẳng đi qua N và song song với PQ.
Mà hai đường thẳng MN và NO đều đi qua N và song song với PQ.
Suy ra hai đường thẳng MN và NO trùng nhau.
Do đó ba điểm M, N, O thẳng hàng.
Vậy ba điểm M, N, O thẳng hàng.
Câu 3:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Tiên đề Euclid được phát biểu là: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Câu 4:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Phát biểu diễn đạt đúng nội dung tiên đề Euclid là: Cho điểm M nằm ngoài đường thẳng a, đường thẳng đi qua M và song song với a là duy nhất. Do đó A đúng.
Phương án B sai vì có vô số đường thẳng song song với đường thẳng cho trước.
Phương án C sai vì qua điểm M ở ngoài đường thẳng a, chỉ có duy nhất một đường thẳng song song với a.
Vậy ta chọn A.
Câu 5:
Cho hình vẽ sau:
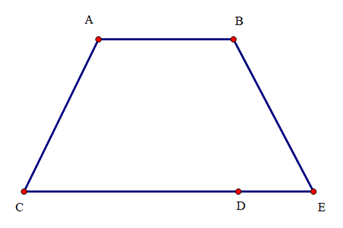
Biết AB // CD. Phát biểu đúng là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có AB // CD.
Mà CD và CE cùng đi qua điểm C nên theo tiên đề Euclid chỉ có một đường thẳng qua C và song song với AB.
Suy ra AB // CE.
Câu 6:
Cho MN // PQ. Gọi A là trung điểm của MN. Khi đó:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
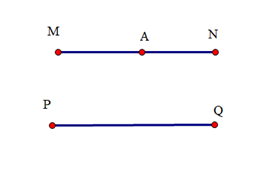
Ta có MN // PQ, A là trung điểm của MN nên A nằm trên đường thẳng MN.
Suy ra:
+ MA và AN trùng nhau. Do đó A sai.
+ MA // PQ (tiên đề Euclid). Do đó B đúng.
+ AN // PQ (tiên đề Euclid). Do đó C sai, D sai.
Vậy ta chọn B.
Câu 7:
Cho tam giác ABC. Qua đỉnh A vẽ đường thẳng a song song với BC, qua đỉnh B vẽ đường thẳng b song song với AC. Số đường thẳng a, b vẽ được lần lượt là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
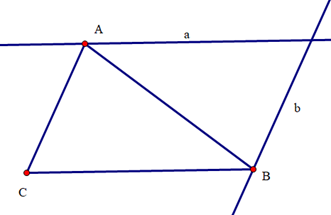
Theo tiên đề Ơclit về đường thẳng song song ta chỉ vẽ được một đường thẳng a qua A và song song với đường thẳng BC, một đường thẳng b qua B và song song với đường thẳng AC.
Vậy ta chọn phương án A.
Câu 8:
Cho đường thẳng c cắt hai đường thẳng song song a và b. Khi đó tiên đề Euclid suy ra tính chất nào sau đây:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Cho đường thẳng c cắt hai đường thẳng song song a và b. Khi đó tiên đề Euclid suy ra các tính chất:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau;
Vậy ta chọn phương án D.
Câu 9:
Cho tam giác ABC. Lấy hai điểm phân biệt M, N sao cho AM // BC; AN // BC như hình vẽ:
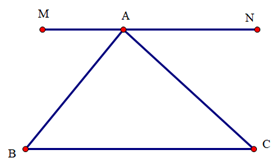
Khi đó:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Theo tiên đề Euclid: chỉ có một đường thẳng đi qua A và song song với BC
Mà hai đường thẳng AM và AN đều đi qua A và song song với BC
Suy ra hai đường thẳng AM và AN trùng nhau
Do đó ba điểm M, A, N thẳng hàng.
Vậy ta chọn phương án D.
Câu 10:
Cho hình vẽ và các khẳng định sau:
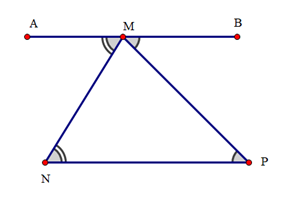
(I). AM // NP;
(II). MB // NP;
(III). A, M, B thẳng hàng.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
+ Ta có \(\widehat {AMN} = \widehat {MNP}\), mà hai góc \(\widehat {AMN}\) và \(\widehat {MNP}\) nằm ở vị trí so le trong
Suy ra AM // NP (dấu hiệu nhận biết)
Do đó (I) đúng.
+ Ta có \(\widehat {BMP} = \widehat {MPN}\), mà hai góc này nằm ở vị trí so le trong
Suy ra MB // NP (dấu hiệu nhận biết)
Do đó (II) đúng.
+ Theo tiên đề Euclid: chỉ có một đường thẳng đi qua M và song song với NP
Mà hai đường thẳng AM và MB đều đi qua M và song song với NP
Suy ra hai đường thẳng AM và MB trùng nhau
Nên ba điểm A, M, B thẳng hàng.
Do đó (III) đúng.
Vậy có ba khẳng định đúng trong các khẳng định trên.
Câu 11:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
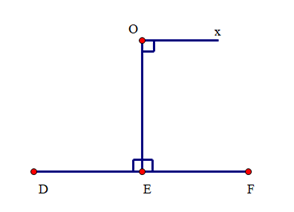
Vì OE ⊥ Ox; OE ⊥ EF nên EF // Ox (vì cùng vuông góc với OE)
Vì OE ⊥ Ox; OE ⊥ DE nên DE // Ox (vì cùng vuông góc với OE)
Theo tiên đề Euclid: chỉ có một đường thẳng đi qua E và song song với Ox
Mà hai đường thẳng DE và EF đều đi qua E và song song với Ox
Suy ra hai đường thẳng DE và EF trùng nhau
Do đó ba điểm D, E, F thẳng hàng.
Vậy ta chọn phương án A.
Câu 12:
Cho đường thẳng xy và một điểm A không thuộc đường thẳng xy. Lấy hai điểm B và C sao cho AB // xy, AC // xy. Khi đó khẳng định nào sau đây đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
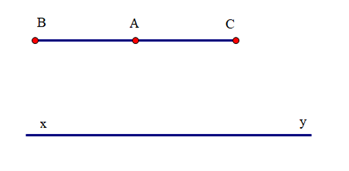
+ Theo tiên đề Euclid: chỉ có một đường thẳng đi qua A và song song với xy
Mà hai đường thẳng AB và AC đều đi qua A và song song với xy
Suy ra hai đường thẳng AB và AC trùng nhau.
Do đó ba điểm A, B, C thẳng hàng.
Suy ra các khẳng định A là đúng, B và D là sai.
Ta xét trường hợp B nằm giữa A và C (hình vẽ)
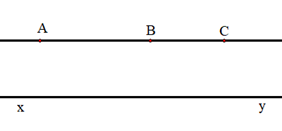
Vì B nằm giữa A và C (theo điều giả sử)
Suy ra AC = AB + BC.
Do đó khẳng định C là sai.
Vậy ta chọn phương án A.