7 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 KNTT Bài 12. Tổng các góc trong một tam giác (Thông hiểu) có đáp án

Trắc nghiệm Toán 7 KNTT Bài 12. Tổng các góc trong một tam giác (Phần 2) có đáp án

Trắc nghiệm Toán 7 KNTT Bài 12. Tổng các góc trong một tam giác (Thông hiểu) có đáp án

650 lượt thi
7 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

∆ABC có $\hat{A} = 75 °, \hat{B} = 45 °$ . Khi đó $\hat{C}$ có số đo bằng:

A. 90°;

B. 60°;

C. 45°;

D. 75°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - \hat{A} - \hat{B} = 180 ° - 75 ° - 45 ° = 60 °$ .

Vậy ta chọn phương án B.

Câu 2:

Cho ∆MNP có $\hat{M} = 80 °$ , biết $\hat{N} - \hat{P} = 40 °$ . Khi đó số đo của $\hat{N}$ bằng:

A. 75°;

B. 45°;

C. 70°;

D. 60°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\hat{N} - \hat{P} = 40 °$ . Suy ra $\hat{P} = \hat{N} - 40 °$ .

∆MNP có $\hat{M} + \hat{N} + \hat{P} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $80 ° + \hat{N} + \hat{N} - 40 ° = 180 °$ .

Do đó $2 \hat{N} = 180 ° - 80 ° + 40 ° = 140 °$ .

Vì vậy $\hat{N} = 140 ° : 2 = 70 °$ .

Vậy ta chọn phương án C.

Câu 3:

Cho ∆ABC có $\hat{A} = 75 °$ và $\hat{B} = 2 \hat{C}$ . Số đo của $\hat{C}$ bằng:

A. 70°;

B. 35°;

C. 40°;

D. 50°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $75 ° + 2 \hat{C} + \hat{C} = 180 °$ .

Do đó $3 \hat{C} = 180 ° - 75 ° = 105 °$ .

Vì vậy $\hat{C} = 105 ° : 3 = 35 °$ .

Vậy ta chọn phương án B.

Câu 4:

Cho hình vẽ bên.

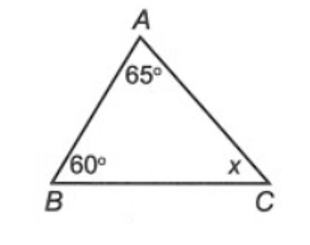
Số đo của x bằng:

A. 60°;

B. 30°;

C. 45°;

D. 55°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra 65° + 60° + x = 180°

Do đó x = 180° – 65° – 60° = 55°.

Vậy ta chọn phương án D.

Câu 5:

Cho hình vẽ bên.

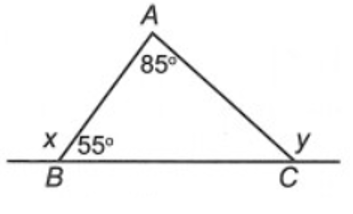
Số đo của x và y là:

A. x = 140° và y = 125°;

B. x = 55° và y = 40°;

C. x = 125° và y = 140°;

D. x = 40° và y = 55°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

⦁ Ta có y được gọi là góc ngoài tại đỉnh C của ∆ABC.

Suy ra $y = \hat{B A C} + \hat{A B C} = 85 ° + 55 ° = 140 °$ .

⦁ Lại có: $x + \hat{B} = 180 °$ (hai góc kề bù)

Suy ra $x = 180 ° - \hat{B} = 180 ° - 55 ° = 125 °$ .

Vậy x = 125° và y = 140°.

Do đó ta chọn phương án C.

Câu 6:

Cho ∆ABC có $\hat{B} = 30 °, \hat{C} = 40 °$ . Khi đó ∆ABC là:

A. Tam giác tù;

B. Tam giác nhọn;

C. Tam giác vuông;

D. Đáp án khác.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{A} = 180 ° - \hat{B} - \hat{C} = 180 ° - 30 ° - 40 ° = 110 ° > 90 °$ .

Vì vậy $\hat{A}$ là góc tù.

Do đó ∆ABC là tam giác tù.

Vậy ta chọn phương án A.

Câu 7:

Kết luận nào sau đây đúng?

A. Một tam giác chỉ có tối đa hai góc nhọn;

B. Một tam giác chỉ có nhiều nhất một góc tù;

C. Trong một tam giác, có ít nhất hai góc có số đo nhỏ hơn 60°;

D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo các góc còn lại.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

⦁ Ta có định nghĩa: Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

Do đó một tam giác có thể có ba góc nhọn.

Vì vậy phương án A sai.

⦁ Giả sử ∆ABC có $\hat{A}$ , $\hat{B}$ là góc tù. Tức là, $\hat{A} > 90 °, \hat{B} > 90 °$ .

Khi đó $\hat{A} + \hat{B} > 180 °$ (mâu thuẫn với định lí tổng ba góc của một tam giác).

Suy ra một tam giác chỉ có thể có một góc tù.

Vì vậy phương án B đúng.

⦁ Giả sử ∆ABC có $\hat{A} < 60 °, \hat{B} < 60 °, \hat{C} < 60 °$ .

Khi đó $\hat{A} + \hat{B} + \hat{C} < 60 ° + 60 ° + 60 ° = 180 °$ (mâu thuẫn với định lí tổng ba góc của một tam giác).

Suy ra, trong một tam giác, có nhiều nhất hai góc có số đo nhỏ hơn 60°.

Vì vậy phương án C sai.

⦁ Giả sử ∆ABC có $\hat{A}$ tù.

Khi đó góc ngoài tại đỉnh A của ∆ABC là góc nhọn.

Tức là, tổng $\hat{B} + \hat{C}$ luôn luôn nhỏ hơn 90°.

Mà $\hat{A} > 90 °$ .

Vì vậy $\hat{A} > 90 ° > \hat{B} + \hat{C}$ (mâu thuẫn với kết luận ở phương án D).

Do đó phương án D sai.

Vậy ta chọn phương án B.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 7 KNTT Bài 12. Tổng các góc trong một tam giác (Phần 2) có đáp án

Trắc nghiệm Toán 7 KNTT Bài 12. Tổng các góc trong một tam giác (Thông hiểu) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương