Cực trị của hàm số và cách giải bài tập – Toán lớp 12

A. LÝ THUYẾT

1. Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) và điểm $x_0\in (a;b)$ .

- Nếu tồn tại số h > 0 sao cho f (x) < f (x₀)  với mọi $x\in (x_0-h;x_0+h)$ và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực đại tại x₀ .

- Nếu tồn tại số h > 0 sao cho f (x) > f (x₀) với mọi $x\in (x_0-h;x_0+h)$ và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực tiểu tại x₀ .

2. Điều kiện cần để hàm số có cực trị.

Định lý 1: Giả sử hàm số f(x) đạt cực trị tại điểm x_o. Khi đó, nếu f(x) có đạo hàm tại điểm x_o thì f‘(x_o) = 0.

Lưu ý:

- Đạo hàm f‘(x) có thể bằng 0 tại điểm x_o nhưng hàm số f(x) không đạt cực trị tại điểm x_o.

- Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.

- Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0, hoặc tại đó hàm số không có đạo hàm.

- Hàm số đạt cực trị tại x_o và nếu đồ thị hàm số có tiếp tuyến tại điểm (x_o ; f(x_o)) thì tiếp tuyến đó song song với trục hoành.

Ví dụ : Hàm số y = |x| và hàm số y = x³

3. Điều kiện đủ để hàm số có cực trị.

Định lý 2: Giả sử hàm số y = f(x) liên tục trên K = ( x₀ -h: x₀ +h ) và có đạo hàm trên K hoặc trên$K\backslash \text{{}{x}_0\text{}}$ , với h >0 .

- Nếu f '(x) > 0 trên khoảng (x₀ - h; x₀) và  trên $(x_0;x_0+h)$ thì x₀ là một điểm cực đại của hàm số f(x) .

- Nếu f '(x) < 0  trên khoảng (x₀ - h; x₀) và f '(x) > 0 trên $(x_0;x_0+h)$ thì x₀ là một điểm cực tiểu của hàm số f(x) .

Minh họa bằng bảng biến thiến

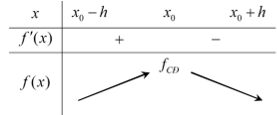
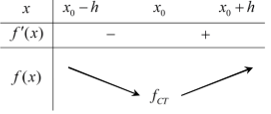
Lưu ý:

- Như vậy: Điểm cực trị phải là một điểm trong của tập hợp D (D ⊂ ℝ). Nếu f’(x) không đổi dấu thì hàm số không có cực trị.

(Nhấn mạnh: x_o ∈ (a; b)⊂ D nghĩa là x_o là một điểm nằm ở giữa trong của D).

Ví dụ: Hàm số  xác định trên D= [0,+∞). Ta có y ≥ y (0) với mọi x, nhưng x = 0 không phải là cực tiểu của hàm số vì D không chứa bất kì 1 lân cận nào của điểm 0.

^- Nếu hàm số y = f (x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f (x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là f _CĐ ( f_CT ), còn điểm M (x₀;f( x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

^- Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

- Giá trị cực đại (cực tiểu) f(x_o) nói chung không phải là GTLN (GTNN) của  f(x) trên tập hợp D.

- Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp D. Hàm số cũng có thể không có điểm cực trị.

- x_o là một điểm cực trị của hàm số f(x) thì điểm (x_o ; f(x_o)) được gọi là điểm cực trị của đồ thị hàm số f(x) .

4. Định lý 3: Giả sử hàm số f  có đạo hàm cấp một trên khoảng (a; b) chứa điểm x_o ;  f ‘(x_o) = 0 và f  có đạo hàm cấp hai khác 0 tại điểm x_o

a) Nếu f ”(x_o) < 0 thì hàm số f  đạt cực đại tại điểm x_o
b) Nếu f ”(x_o) < 0 thì hàm số f  đạt cực tiểu tại điểm x_o

Lưu ý:

- Không cần xét hàm số f(x) có hay không có đạo hàm tại điểm x = x_o nhưng không thể bỏ qua điều kiện hàm số liên tục tại điểm x_o.

B. CÁC KỸ NĂNG GIẢI TOÁN CƠ BẢN.

1. Quy tắc tìm cực trị của hàm số.

Quy tắc 1.

Bước 1:  Tìm tập xác định của hàm số.

Bước 2: Tính f '(x) . Tìm các điểm tại đó f '(x) bằng 0 hoặc f '(x) không xác định.

Bước 3: Lập bảng biến thiên.

Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2.

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính f '(x) . Giải phương trình f '(x) và ký hiệu x_i= $(i=1,2,3,\mathrm{...})$ là các nghiệm.

Bước 3: Tính  f ”(x) và f ”(x_i ) .

Bước 4: Dựa vào dấu của f ”(x_i ) suy ra tính chất cực trị của điểm x_i .

2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba 

 $y=a{x}^3+b{x}^2+cx+d$ ($a\ne 0$).

- Ta có $y^{\text{'}}=3a{x}^2+2bx+c$

Đồ thị hàm số có 2 điểm cực trị khi phương trình y' = 0 có hai nghiệm phân biệt .

$\iff b^2-3ac>0$

Và không có cực trị ⇔Δ’ = b²  − 3ac ≤ 0

- Cho hàm số $y=a{x}^3+b{x}^2+cx+d$ có hai điểm cực trị phân biệt là A, B . Khi đó:

Phương trình đường thẳng AB : y = $\frac{2}{3}$(c -$\frac{2b}{3a}$ )x + (d -$\frac{bc}{9a}$)

Độ dài đoạn thẳng AB = $\sqrt{\frac{4e+ 16e^3}{a}}$ với e = $\frac{b^2-3ac}{9a}$

Hoặc khi đó đường thẳng qua hai điểm cực trị liên quan tới: $y-\frac{y^{\text{'}}.y^{\text{'}\text{'}}}{18a}$ (CASIO hỗ trợ).

3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.

Cho hàm số: $y=a{x}^4+b{x}^2+c$ ($a\ne 0$) có đồ thị là (C) .

Ta có $y^{\text{'}}=4a{x}^3+2bx;$

$\hspace{0.17em}{y}^{\text{'}}=0\iff \left[\begin{array}{l}x=0\\ x^2=-\frac{b}{2a}\end{array}\right.$

(C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt $\iff -\frac{b}{2a}>0$ hay ab < 0

Hàm số có 3 cực trị là:

$$\begin{gathered} A(0;c), \\ B\left(-\sqrt{-\frac{b}{2a}};-\frac{\Delta }{4a}\right), \\ C\left(\sqrt{-\frac{b}{2a}};-\frac{\Delta }{4a}\right) \end{gathered}$$.

Độ dài các đoạn thẳng: 

$$\begin{gathered} AB=AC=\sqrt{\frac{b^4}{16a^2}-\frac{b}{2a}}, \\ BC=2\sqrt{-\frac{b}{2a}} \end{gathered}$$.

C. CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Tìm các điểm cực trị của hàm số.

1. Phương pháp giải.

Quy tắc 1: Áp dụng định lý 2

- Tìm  f’(x)

- Tìm các điểm x_i (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm

- Xét dấu của  f’(x). Nếu  f’(x) đổi dấu khi x qua điểm x_o  thì hàm số có cực trị tại điểm x_o

Quy tắc 2: Áp dụng định lý 3

- Tìm  f’(x)

- Tìm các nghiệm x_i (i = 1, 2, 3,…) của phương trình f ‘(x) = 0 

- Với mỗi x_i tính f ”(x_i)

- Nếu f ”(x_i) < 0 thì hàm số đạt cực đại tại điểm x_i

- Nếu f ”(x_i) > 0 thì hàm số đạt cực tiểu tại điểm x_i

2. Ví dụ minh hoạ.

Ví dụ 1. (Đề thi THPTQG năm 2021) Cho hàm số  có bảng biến thiên như sau:

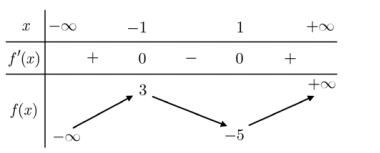
Giá trị cực đại của hàm số đã cho là

A. 3                          

B. -1                

C. -5                             

D. 1 

Lời giải

Dựa vào bảng biến thiên, giá trị cực đại của hàm số là $y=f(-1)=3$.

Chọn A.

Ví dụ 2. (Đề tốt nghiệp 2020 - Đợt 2 Mã đề 103) Cho hàm số  có đạo hàm . Số điểm cực đại của hàm số đã cho là:

A. 2                                     

B. 3

C. 4                      

D. 1

Lời giải

$$\begin{gathered} f^{\text{'}}\left(x\right)=0\iff x\left(x+1\right){\left(x-4\right)}^3=0 \\ \iff \left[\begin{array}{l}x=0\\ x=-1\\ x=4\end{array}\right. \end{gathered}$$

Lập bảng biến thiên của hàm số

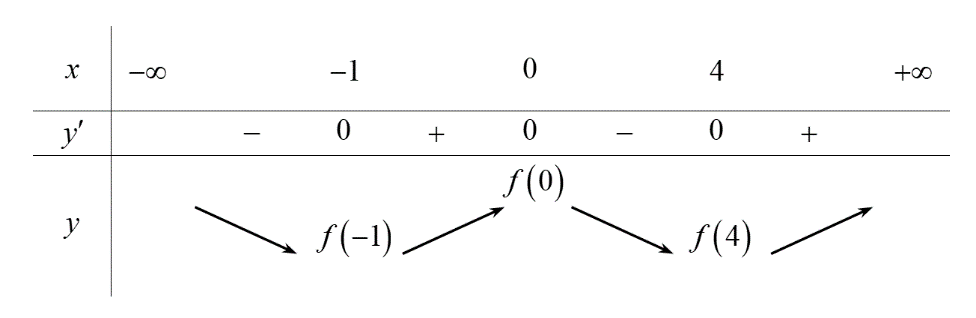
Vậy hàm số đã cho có một điểm cực đại.

Chọn D.

Ví dụ 3. (Đề tốt nghiệp 2020 - Đợt 1 Mã đề 101) Cho hàm số bậc bốn  có bảng biến thiên như sau:

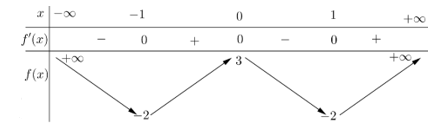
Số điểm cực trị của hàm số  là

A. 11                                    

B. 9                      

C. 7                       

D. 5

Lời giải

Ta chọn hàm $f\left(x\right)=5x^4-10x^2+3$.

Đạo hàm

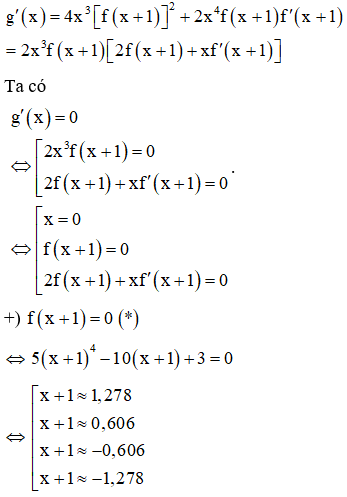
$\Rightarrow$Phương trình có bốn nghiệm phân biệt khác 0.

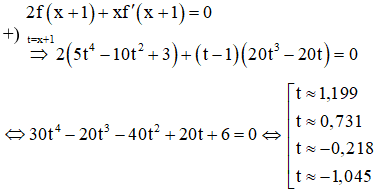
$\Rightarrow$Phương trình có bốn nghiệm phân biệt khác 0 và khác các nghiệm của phương trình ( *)

Vậy số điểm cực trị của hàm số g(x) là 9.

Chọn B.

Ví dụ 4. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=-2x^3+3x^2+1$.

A. $y=x-1.$

B. $y=x+1.$

C. $y=-x+1.$

D. $y=-x-1.$

Lời giải

Ta có :

$$\begin{gathered} y^{\text{'}}=-6x^2+6x;y^{\text{'}}=0 \\ \iff \left[\begin{array}{l}x=0\Rightarrow y=1\\ x=1\Rightarrow y=2\end{array}\right.. \end{gathered}$$

Suy ra đồ thị hàm số đã hai điểm cực trị là A(0;1) và B(1;2).

Khi đó, đường thẳng đi qua hai điểm cực trị chính là đường thẳng AB có phương trình  $y=x+1.$

Chọn B.

Cách 2. Lấy  chia cho , ta được :

$\iff y=\frac{1}{3}\left(x-\frac{1}{2}\right)y^{\text{'}}+x+1$

Suy ra phương trình đường thẳng đi qua hai điểm cực trị là phần dư trong phép chia, đó là $y=x+1$

3. Bài tập tự luyện.

Câu 1. Cho hàm số f(x) xác định, liên tục và có đạo hàm trên khoảng (a,b). Mệnh đề nào sau đây là sai?

A. Nếu f(x) đồng biến trên (a,b) thì hàm số không có cực trị trên (a,b).

B. Nếu f(x) nghịch biến trên (a,b) thì hàm số không có cực trị trên (a,b).

C. Nếu f(x) đạt cực trị tại điểm $x_0\in \left(a;b\right)$ thì tiếp tuyến của đồ thị hàm số tại điểm $M\left(x_0;f\left(x_0\right)\right)$ song song hoặc trùng với trục hoành.

D. Nếu f(x) đạt cực đại tại $x_0\in \left(a;b\right)$ thì f(x) đồng biến trên $\left(a;x_0\right)$ và nghịch biến trên $\left(x_0;b\right)$.

Câu 2. Cho khoảng (a,b) chứa điểm $x_0$, hàm số f(x) có đạo hàm trên khoảng (a,b) (có thể trừ điểm $x_0$ ). Mệnh đề nào sau đây là đúng?

A. Nếu f(x) không có đạo hàm tại $x_0$ thì f(x) không đạt cực trị tại $x_0$.

B. Nếu $f\text{'}\left(x_0\right)=0$ thì f(x) đạt cực trị tại điểm $x_0$.

C. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)=0$ thì f(x) không đạt cực trị tại điểm $x_0$.

D. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)\ne 0$ thì f(x) đạt cực trị tại điểm $x_0$.

Câu 3. Phát biểu nào sau đây là đúng?

A. Nếu $f\text{'}\left(x\right)$ đổi dấu từ dương sang âm khi x qua điểm $x_0$ và f(x) liên tục tại $x_0$ thì hàm số y= f (x) đạt cực đại tại điểm $x_0$.

B. Hàm số y= f (x) đạt cực trị tại $x_0$ khi và chỉ khi $x_0$ là nghiệm của $f\text{'}\left(x\right)=0.$

C. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)=0$ thì $x_0$ không là điểm cực trị của hàm số y= f (x).

D. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)>0$ thì hàm số đạt cực đại tại $x_0$.

Câu 4. Giả sử hàm số y= f (x) có đạo hàm cấp hai trong khoảng $\left(x_0-h;x_0+h\right),$ với h >0  Khẳng định nào sau đây là sai?

A. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)>0$ thì $x_0$ là điểm cực tiểu của hàm số.

B. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)<0$ thì $x_0$ là điểm cực đại của hàm số.

C. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)=0$ thì $x_0$ không là điểm cực trị của hàm số.

D. Nếu $f\text{'}\left(x_0\right)=0$ và $f\text{'}\text{'}\left(x_0\right)=0$ thì chưa kết luận được $x_0$ có là điểm cực trị của hàm số.

Câu 5. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Cho hàm số f(x) có bảng biến thiên như sau :

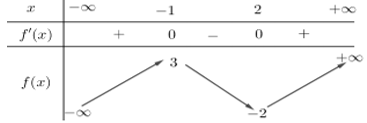
Điểm cực đại của hàm số đã cho là 

A. x = 3

B. x = 2

C. x = -2

D. x = -1

Câu 6. (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101) Cho hàm f(x) có bảng biến thiên như sau:

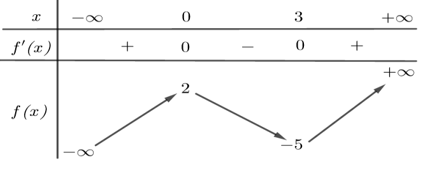
Giá trị cực tiểu của hàm số đã cho bằng

A. 3

B. -5

C.  0

D. 2

Câu 7. (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101) Cho hàm số f(x) liên tục trên $ℝ$ và có bảng xét dấu của $f^{\text{'}}\left(x\right)$ như sau:

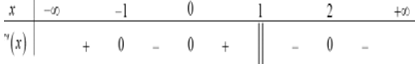
Số điểm cực đại của hàm số đã cho là

A. 4

B. 1

C. 2

D. 3

Câu 8. Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau:

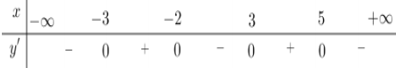
Số điểm cực trị của hàm số đã cho là

A. 5

B. 3

C. 2

D. 4.

Câu 9. Cho hàm số có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng:

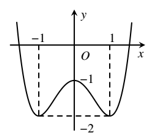
A. –1

B. –2.

C. 1.

D. 0.

Câu 10. Cho hàm số y=f(x) có đồ thị như hình vẽ. Đồ thị hàm số y=f(x) có mấy điểm cực trị?

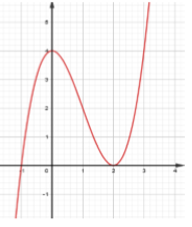
A. 0

B. 2

C. 1

D. 3

Câu 11. Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên.

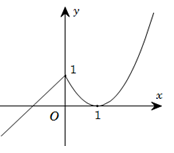
Hỏi hàm số có bao nhiêu điểm cực trị?

A. 0.

B. 1.

C. 3.

D. 2.

Câu 12. Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên.

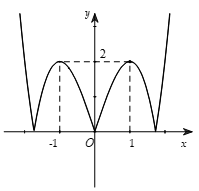
Hỏi hàm số có bao nhiêu điểm cực trị?

A. 2. 

B. 3.

C. 4.

D. 5.

Câu 13. Hàm số $y=2x^3-x^2+5$ có điểm cực đại là:

A. $x=\frac{1}{3}$

B. 5

C. 3

D. 0

Câu 14. Tìm số điểm cực trị của đồ thị hàm số $y=\frac{x-2}{x+1}$?

A.4.

B. 1.

C. 0.

D. 3.

Câu 15. Hàm số $y=-x^4-x^2+1$ có mấy điểm cực trị?

A. 3.

B. 0.

C. 1.

D. 2.

Câu 16. Gọi $x_1,x_2$ là hai điểm cực trị của hàm số $f\left(x\right)=\frac{1}{3}{x}^3-3x^2-2x$. Giá trị của $x_1^2+x_2^2$ bằng:

A. 13

B. 32

C. 4

D. 36

Câu 17. Điểm cực tiểu của đồ thị hàm số $y=3x^4-4x^3-6x^2+12x+1$ là điểm $M\left(x_0;y_0\right).$ Tính tổng  $T=x_0+y_0.$

A. T= 8

B. T=4

C. T=-11

D. T=3

Câu 18. Đồ thị hàm số nào sau đây có đúng 1 điểm cực trị?

A. $y=-x^4-3x^2+4$

B. $y=x^3-6x^2+9x-5$

C. $y=x^3-3x^2+3x-5$

D. $y=2x^4-4x^2+1$

Câu 19. Đồ thị hàm số  nào sau đây có 3 điểm cực trị?

A. $y=2x^4-4x^2+1.$

B. $y={(x^2+1)}^2.$

C. $y=x^3-6x^2+9x-5.$

D. $y=-x^4-3x^2+4.$

Câu 20. Cho hàm số $y=f\left(x\right)$liên tục trên R và có đạo hàm $f^{\text{'}}\left(x\right)=\frac{\left(x-1\right){\left(x-2\right)}^2{\left(x-3\right)}^5}{\sqrt[3]{x-4}}$. Hỏi hàm số  y= f(x) có bao nhiêu điểm cực trị?

A. 2

B. 4

C. 3

D. 5.

Câu 21. Gọi $y_1,y_2$ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số $y=x^3-3x^2-9x+4$. Tính $P=y_1.y_2.$

A. P=-302

B. P=- 82

C. P=-207

D.P= 25

Câu 22. Tính khoảng cách  giữa hai điểm cực trị của đồ thị hàm số $y=\left(x+1\right){\left(x-2\right)}^2$

A. $d=2\sqrt{5}$

B. $d=2$

C. $d=4$

D. $d=5\sqrt{2}$.

Câu 23. (ĐỀ CHÍNH THỨC 2016 – 2017) Đường cong ở hình bên là đồ thị của hàm số $y=a{x}^4+b{x}^2+c$ với a,b,c là các số thực.

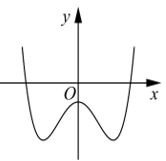
Mệnh đề nào dưới đây là đúng ?

A. Phương trình $y^{\text{'}}=0$ vô nghiệm trên tập số thực.

B. Phương trình $y^{\text{'}}=0$ có đúng một nghiệm thực.

C. Phương trình $y^{\text{'}}=0$ có đúng hai nghiệm thực phân biệt.

D. Phương trình  $y^{\text{'}}=0$có đúng ba nghiệm thực phân biệt.

Câu 24. Cho hàm số $y=f\left(x\right)$ liên tục tại $x_0$ và có bảng biến thiên sau:

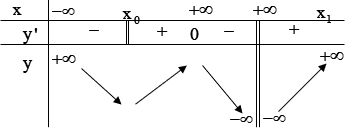
Mệnh đề nào sau đây là đúng?

A. Hàm số có hai điểm cực đại, một điểm cực tiểu.   

B. Hàm số có một điểm cực đại, không có điểm cực tiểu.

C. Hàm số có một điểm cực đại, hai điểm cực tiểu.   

D. Hàm số có một điểm cực đại, một điểm cực tiểu.

Câu 25*. Cho hàm số $y=f\left(x\right)$ có bảng biến thiên sau:

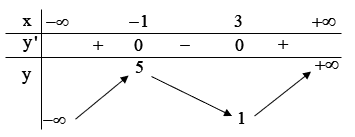
Hàm số $y=\left|f\left(x\right)\right|$ có bao nhiêu điểm cực trị ?

A. 5

B. 3

C. 4

D. 2

Câu 26. (ĐỀ THPT QG 2017)  Đồ thị của hàm số y = x³ – 3x² – 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?

A. $P(1;0)$

B. $M(0;-1)$

C. $N(1;-10)$

D. $Q(-1;10)$

Câu 27. (ĐỀ THPT QG 2017)  Đồ thị của hàm số y = – x³ + 3x² + 5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.

A. $60°$

B. $S=\frac{10}{3}$

C. $V=\frac{9a^3}{8}$

D. $V=\frac{a^3}{8}$

Câu 28. Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số $y=\left(x+1\right){\left(x-2\right)}^2$ là:

A. $2\sqrt{5}$

B. 2.

C. 4.

D. $5\sqrt{2}$.

Câu 29. Trong các đường thẳng dưới đây, đường thẳng nào đi qua trung điểm đoạn thẳng nối các điểm cực trị của đồ thị hàm số $y=x^3-3x^2+1$?

A. $y=2x-3$

B. $y=-\frac{x}{3}+\frac{1}{3}$

C. $y=2x+3$

D. $y=-2x-1$.

Câu 30. Đồ thị hàm số $y=x^4-x^2+1$ có bao nhiêu điểm cực trị có tung độ dương?

A. 1

B. 2

C. 3

D. 4.

Câu 31. Cho hàm số $f\left(x\right)={\left(x^2-3\right)}^2$. Giá trị cực đại của hàm số  bằng:

A. 8.

B. - 8

C. 0.

D. $\frac{1}{2}$.

Câu 32. Điểm cực trị của hàm số $y=\sin 2x-x$ là:

A. $x_{\text{CD}}=\frac{\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$

B. $x_{\text{CT}}=-\frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$.

C. $x_{\text{CD}}=\frac{\pi }{6}+k\pi ;x_{\text{CT}}=-\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$

D. $x_{\text{CD}}=\frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$.

Câu 33. Giá trị cực đại của hàm số $y=x+2\cos x$ trên khoảng $\left(0;\pi \right)$ là:

A. $\frac{5\pi }{6}+\sqrt{3}$

B. $\frac{5\pi }{6}-\sqrt{3}$

C. $\frac{\pi }{6}+\sqrt{3}$

D. $\frac{\pi }{6}-\sqrt{3}$.

Câu 34. Cho hàm số $y=\sin x-\sqrt{3}\cos x$. Khẳng định nào sau đây sai:

A. $x=\frac{5\pi }{6}$ là một nghiệm của phương trình.

B. Trên khoảng $\left(0;\pi \right)$ hàm số có duy nhất một cực trị.

C. Hàm số đạt cực tiểu tại $x=\frac{5\pi }{6}$.

D. $y+y\text{'}\text{'}=0,\forall x\in ℝ$.

Câu 35. Độ giảm huyết áp của một bệnh nhân được đo bởi công thức $G\left(x\right)=0,025x^2\left(30-x\right)$ trong đó x(mg) và x > 0 là liều lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng:

A. 15mg.

B. 30mg.

C. 40mg.

D. 20mg.

Câu 36. Hỏi hàm số $y={\left|x\right|}^3-3x+1$ có tất cả bao nhiêu điểm cực trị?

A. Không có điểm cực trị.

B. Có một điểm cực trị.

C. Có hai điểm cực trị.

D. Có ba điểm cực trị.

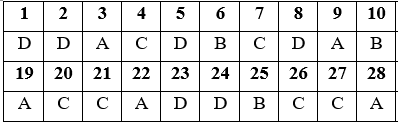
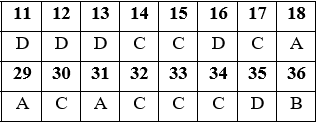
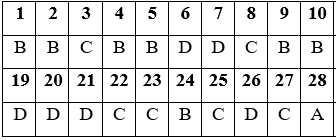
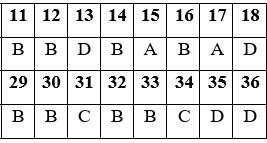
Đáp án

Dạng 2: Tìm điều kiện để hàm số có cực trị.

1. Phương pháp.

Sử dụng định lí 2 và định lí 3

a, Cực trị của hàm số bậc ba:

Cho hàm số y = ax³ + bx² + cx + d, a ≠ 0.

y’ = 0 ⇔ 3ax² + 2bx + c = 0 (1) ; Δ’_y’ = b² – 3ac

 - Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.

→ Hàm số bậc 3 không có cực trị ⇔ b² – 3ac ≤ 0

 - Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.

→ Hàm số bậc 3 có 2 cực trị ⇔ b² – 3ac > 0

b, Cực trị của hàm số bậc bốn trùng phương:

Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

y' = 4ax³ + 2bx;  y' = 0

⇔ $\left[\begin{array}{l}x=0\\ x^2=-\frac{b}{2a}\end{array}\right.$

- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Chú ý

* Hàm số f (xác định trên D) có cực trị ⇔ ∃ x_o ∈ D thỏa mãn hai điều kiện sau:

- Tại đạo hàm của hàm số tại x_o phải bằng 0 hoặc hàm số không có đạo hàm tại x_o

- f ‘(x) phải đổi dấu qua điểm x_o hoặc f ”(x_o) ≠ 0.

2. Ví dụ minh hoạ.

Ví dụ 1. Tìm tất cả các giá trị của tham số m để hàm số $y=x^3-3m{x}^2+6mx+m$ có hai điểm cực trị.

A. $m\in \left(0;2\right)$

B. $m\in \left(-\infty ;0\right)\cup \left(8;+\infty \right)$.         

C. $m\in \left(-\infty ;0\right)\cup \left(2;+\infty \right)$ q

D. $m\in \left(0;8\right)$.

Lời giải

Ta có $y\text{'}=3x^2-6mx+6m$

$=3\left(x^2-2mx+2m\right)$

Để hàm số có hai điểm cực trị $\iff x^2-2mx+2m=0$ có hai nghiệm phân biệt

$$\begin{gathered} \iff \Delta \text{'}=m^2-2m>0 \\ \iff \left[\begin{array}{l}m<0\\ m>2\end{array}\right.. \end{gathered}$$

Chọn C.

Ví dụ 2. Cho hàm số $y=a{x}^4+b{x}^2+c\left(a\ne 0\right)$ . Với điều kiện nào của các tham số a,b,c thì hàm số có ba điểm cực trị?

A.  a,b cùng dấu và c bất kì.

B. a,b trái dấu và c bất kì.

C. b=0 và a,c bất kì.

D. c=0 và a,b bất kì.

Lời giải

Ta có :

$$\begin{gathered} y\text{'}=4a{x}^3+2bx=2x\left(2a{x}^2+b\right); \\ y\text{'}=0\iff \left[\begin{array}{l}x=0\\ x^2=-\frac{b}{2a}\end{array}\right.. \end{gathered}$$

Để hàm số có ba điểm cực trị $\iff x^2=-\frac{b}{2a}$ có hai nghiệm phân biệt khác 0

$\iff -\frac{b}{2a}>0\iff ab<0$

Khi đó a,b trái dấu và c bất kì.

Chọn B.

Ví dụ 3. Tìm tất cả các giá trị thực của tham số m để hàm số $y=m{x}^4+\left(m+1\right)x^2+1$ có một điểm cực tiểu.

A. $m>0.$

B. $m\ge 0.$

C. $-1<m<0.$

D. $m>-1.$

Lời giải

TH1. Với $a=0\iff m=0$, khi đó $y=x^2+1$ có đồ thị là một parabol có bề lõm quay lên nên hàm số có duy nhất một điểm cực tiểu.

$\underset{}{\to }m=0$ thỏa mãn.

 

Chọn D.

Nhận xét. Bài toán hỏi hàm số có một điểm cực tiểu nên hàm số có thể có điểm cực đại hoặc không có điểm cực đại. Khi nào bài toán hỏi hàm số có đúng một cực tiểu và không có cực đại thì lúc đó ta chọn đáp án B.

Ví dụ 4. Cho hàm số $y=\frac{1}{3}{x}^3-\frac{1}{2}\left(3m+2\right)x^2+\left(2m^2+3m+1\right)x-4$. Tìm giá trị thực của tham số m để hàm số có hai điểm cực trị là x=3 và x=5.

A. m=0

B. m= 1

C. m=2

D. m=3.

Lời giải

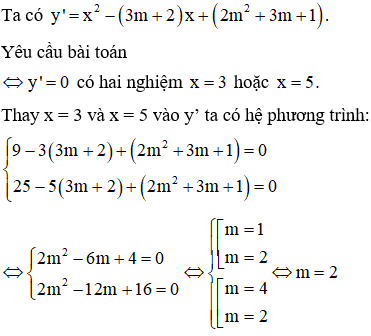
Chọn C.

Ví dụ 5. Cho hàm số $y=2x^3+b{x}^2+cx+1.$ Biết $M\left(1;-6\right)$ là điểm cực tiểu của đồ thị hàm số. Tìm toạ độ điểm cực đại N của đồ thị hàm số.

A. $N\left(2;21\right).$

B. $N\left(-2;21\right).$

C. $N\left(-2;11\right).$

D. $N\left(2;6\right).$

Lời giải

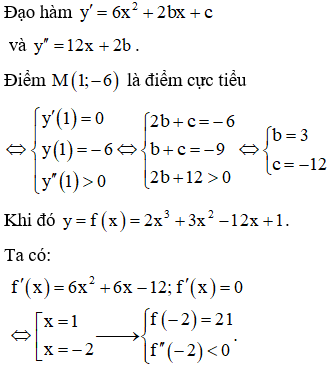
Suy ra N(-2;21) là điểm cực đại của đồ thị hàm số.

Chọn B.

3. Bài tập tự luyện.

Câu 1. Hàm số $y=x^3-(m+2)x+m$ đạt cực tiểu tại x = 1 khi:

A. m = -1

B. m = 2

C. m = -2

D. m = 1

Câu 2. Tìm giá trị thực của tham số m để hàm số $y=x^3-3x^2+mx$ đạt cực đại tại x =0 

A. m = 1

B. m = 2

C. m = -2

D. m = 0

Câu 3.  Biết rằng đồ thị hàm số $y=a{x}^4+b{x}^2+c\left(a\ne 0\right)$ có điểm đại $A\left(0;-3\right)$ và có điểm cực tiểu $B\left(-1;-5\right)$. Mệnh đề nào sau đây là đúng?

A. $\left\{\begin{array}{l}a=-3\\ b=-1\\ c=-5\end{array}\right..$

B. $\left\{\begin{array}{l}a=2\\ b=-4\\ c=-3\end{array}\right..$

C. $\left\{\begin{array}{l}a=2\\ b=4\\ c=-3\end{array}\right..$

D. $\left\{\begin{array}{l}a=-2\\ b=4\\ c=-3\end{array}\right..$

Câu 4. Cho hàm số $y=a{x}^4+b{x}^2+1$ (a ≠ 0). Để hàm số có một cực tiểu và hai cực đại thì a, b  cần thỏa mãn:

A. $a<0,b<0$

B. $a<0,b>0$

C. $a>0,b<0$

D. $a>0,b>0$

Câu 5. Cho hàm số $y=a{x}^4+b{x}^2+1$ (a ≠ 0). Để hàm số chỉ có một cực trị và là cực tiểu thì a, b cần thỏa mãn:

A. $a<0,b\le 0$

B. $a<0,b>0$

C. $a>0,b<0$

D. $a>0,b\ge 0$

Câu 6. Hàm số $y=x^4+2m{x}^2+m^2+m$ có ba cực trị khi:

A. $m=0.$

B. $m>0.$

C. $m<0.$

D. $m\ne 0.$

Câu 7. Đồ thị hàm số $y=x^4-3x^2+ax+b$ có điểm cực tiểu A(2;-2). Tìm tổng a + b.

A. - 14.

B. 14.

C. - 20.

D. 34.

Câu 8. Đồ thị hàm số $y=a{x}^4+b{x}^2+c$ có điểm đại A(0;-3) và có điểm cực tiểu  B(-1; - 5). Khi đó giá trị của a, b, c  lần lượt là:

A. $-3;-1;-5$

B. $2;-4;-3$

C. $2;4;-3$

D. $-2;4;-3$

Câu 9. Hàm số $y=\frac{x^2+mx-1}{x-1}$ có cực đại và cực tiểu thì điều kiện của m là:

A. $m<0$

B. $m=0$

C. $m\in ℝ$

D. $m>0$

Câu 10. Hàm số $y=\frac{x^2+mx+m}{x+m}$ đạt cực đại tại x= 2 khi giá trị thực m bằng:

A. -1

B. -3

C. 1

D. 3 .

Câu 11. Hàm số $y=\sin 3x+m\sin x$ đạt cực đại tại $x=\frac{\pi }{3}$ khi m bằng:

A. 5.

B. -6

C. 6.

D. -5.

Câu 12. Biết hàm số $y=a\sin x+b\cos x+x$ $\left(0<x<2\pi \right)$ đạt cực trị tại $x=\frac{\pi }{3};x=\pi$. Khi đó tổng a + b bằng:

A. 3.

B. $\frac{\sqrt{3}}{3}+1$

C. $\sqrt{3}+1$

D. $\sqrt{3}-1$ 

Câu 13. Tìm tất cả các giá trị của tham số m để hàm số $y=\frac{m}{3}{x}^3+x^2+x+2017$ có cực trị.

A. $m\in \left(-\infty ;1\right]$

B. $m\in \left(-\infty ;0\right)\cup \left(0;1\right)$

C. $m\in \left(-\infty ;0\right)\cup \left(0;1\right]$

D. $m\in \left(-\infty ;1\right)$

Câu 14. Biết rằng hàm số $y={\left(x+a\right)}^3+{\left(x+b\right)}^3-x^3$ có hai điểm cực trị. Mệnh đề nào sau đây là đúng?

A. $ab>0$

B. $ab<0$

C. $ab\ge 0$

D. $ab\le 0$.

Câu 15. Tìm các giá trị của tham số m để hàm số $y=\left(m-3\right)x^3-2m{x}^2+3$ không có cực trị.

A. m=3

B. m=3, m=0.

C. m=0

D. $m\ne 3$

Câu 16. Cho hàm số $y=a{x}^3+b{x}^2+cx+d$. Biết $M\left(0;2\right)$, $N\left(2;-2\right)$ là các điểm cực trị của đồ thị hàm số. Tính giá trị của hàm số tại $x=-2$.

A. $y\left(-2\right)=2$

B. $y\left(-2\right)=22$

C. $y\left(-2\right)=6$

D. $y\left(-2\right)=-18$

Câu 17. Biết rằng hàm số  $y=a{x}^3+b{x}^2+cx$  nhận $x=-1$ là một điểm cực trị. Mệnh đề nào sau đây là đúng?

A. $a+c=b$

B. $2a-b=0$

C. $3a+c=2b$

D.  $3a+2b+c=0$

Câu 18. Cho hàm số $y=\frac{x^3}{3}-\left(m+1\right)x^2+\left(m^2-3\right)x+1$ với m là tham số thực. Tìm tất cả các giá trị của m để hàm số đạt cực trị tại $x=-1$.

A. m=0

B. m=-2

C. m=0, m=-2

D. m=0, m= 2

Câu 19. Biết rằng hàm số $y=3x^3-m{x}^2+mx-3$ có một điểm cực trị $x_1=-1$. Tìm điểm cực trị còn lại $x_2$ của hàm số.

A. $x_2=\frac{1}{4}$

B. $x_2=\frac{1}{3}$

C.$x_2=-\frac{1}{3}$

D. $x_2=-2m-6.$

Câu 20. Cho hàm số $y=x^3-3m{x}^2+3\left(m^2-1\right)x-3m^2+5$ với m là tham số thực. Tìm tất cả các giá trị của m để hàm số đạt cực đại tại x=1.

A. m=0, m=2

B. m=2

C. m=1

D. m=0

Câu 21. Hàm số $y=x^3-3m{x}^2+6mx+m$ có hai điểm cực trị khi m thỏa mãn điều kiện:

A. $0<m<2$

B. $\left[\begin{array}{l}m<0\\ m>8\end{array}\right.$

C. $\left[\begin{array}{l}m<0\\ m>2\end{array}\right..$

D.$0<m<8$

Câu 22. Hàm số $y=\frac{m}{3}{x}^3+x^2+x+2017$ có cực trị khi và chỉ khi:

A. $m\le 1$

B. $\left\{\begin{array}{l}m<1\\ m\ne 0\end{array}\right.$

C. $\left\{\begin{array}{l}m\le 1\\ m\ne 0\end{array}\right.$

D. $m<1$

Câu 23. Với điều kiện nào của a và b để hàm số $y={\left(x+a\right)}^3+{\left(x+b\right)}^3-x^3$ đạt cực đại và cực tiểu ?

A. ab >0.

B. ab < 0.

C. ab ≥ 0.

D. ab ≤ 0.

Câu 24. Hàm số $y=\left(m-3\right)x^3-2m{x}^2+3$ không có cực trị khi:

A. m = 3.

B. m = 0 hoặc m = 3.

C. m = 0.

D. m ≠3.

Câu 25. Tìm tất cả các giá trị của m để hàm số $y=\frac{1}{3}{x}^3-\frac{1}{2}\left(3m+2\right)x^2+\left(2m^2+3m+1\right)x-4$ đạt cực trị tại x = 3 hoặc x = 5, ta được.

A. m = 0.

B. m = 1.

C. m = 2.

D. m = 3.

Câu 26. (ĐỀ THPT QG 2017) Tìm giá trị thực của tham số m để hàm số $y=\frac{1}{3}{x}^3-m{x}^2+\left(m^2-4\right)x+3$ đạt cực đại tại x = 3.

A. m = 0.

B. m = 3.

C. m = 5.

D. m = 1.

Câu 27. Tìm tất cả các giá trị thực của tham số m để hàm số $y=x^4+2m{x}^2+m^2+m$ có ba điểm cực trị.

A. $m=0.$

B. $m>0.$

C. $m<0.$

D. $m\ne 0.$

Câu 28. Tìm tất cả các giá trị của tham số m để hàm số $y=m{x}^4+\left(m-1\right)x^2+1-2m$ có đúng một điểm cực trị.

A. $m\in \left[1;+\infty \right)$

B. $m\in \left(-\infty ;0\right]$

C. $m\in \left[0;1\right]$

D. $m\in \left(-\infty 0\right]\cup \left[1;+\infty \right)$

Câu 29. Cho hàm số $y=x^3-3x^2-9x+m$. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.

A. $y=-8x+m$

B. $y=-8x+m-3$

C. $y=-8x+m+3$

D. $y=-8x-m+3$

Câu 30. Biết rằng đồ thị hàm số $y=x^4-3x^2+ax+b$ có điểm cực tiểu là $A\left(2;-2\right)$. Tính tổng $S=a+b.$

A. $S=-14$

B. $S=14$

C. $S=-20$

D. $S=34$

Đáp án

Dạng 3: Tìm điều kiện để các điểm cực trị của hàm số thỏa mãn điều kiện cho trước.

1. Phương pháp giải.

a, Hàm số bậc ba y = ax³ + bx² + cx + d (a ≠ 0, a, b, c, d phụ thuộc vào tham số)
Bước 1: Tính y’ = 3ax² + 2bx + c, y’ = 0  ⇔ 3ax² +2bx + c = 0 (1)

Để hàm số có cực đại, cực tiểu  ⇔ y’ = 0 có hai nghiệm phân biệt 

⇔ (1) có hai nghiệm phân biệt

⇔ Giá trị tham số thuộc miền D nào đó (*)

Bước 2: Từ điều kiện cho trước dẫn tới một phương trình hoặc một bất phương trình theo tham số, giải phương trình này ta được tham số sau đó đối chiếu với điều kiện (*) và kết luận.

Một số điều kiện thường gặp: (Không dùng dấu tương đương như vậy)

- Để hàm số y = f(x) có 2 cực trị ⇔ a ≠ 0, Δy′ > 0 hoặc a ≠ 0, Δ_y′ > 0

- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục hoành ⇔ y_CD.y_CT  < 0

- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục tung ⇔ x_CD.x_CT < 0

- Để hàm số y = f(x) có 2 cực trị nằm phía trên trục hoành ⇔ y_CD+y_CT > 0 và y_CD.y_CT > 0

- Để hàm số  y = f(x) có 2 cực trị nằm phía dưới trục hoành ⇔ y_CD+y_CT < 0 và y_CD.y_CT > 0

- Để hàm số  y = f(x) có cực trị tiếp xúc với trục hoành ⇔ y_CD.y_CT = 0

- Đồ thị có 2 điểm cực trị khác phía đối với đường thẳng d: Ax + By + C = 0

+ Gọi M₁(x₁; y₁) và M₂(x₂; y₂) là cực đại và cực tiểu của đồ thị hàm số.

+ Gọi t₁ và t₂ là các giá trị khi thay M₁ và M₂ vào đường thẳng d:

t₁ = Ax₁ + By₁ + C; t₂ = Ax₂ + By₂ + C

+ Đồ thị có 2 điểm cực đại, cực tiểu nằm ở hai phía của đường thẳng d:

⇔ y′ = 0 có 2 nghiệm phân biệt và t₁t₂ < 0

+ Đồ thị có 2 điểm cực đại, cực tiểu nằm ở cùng một phía của đường thẳng d:

⇔ y′ = 0 có 2 nghiệm phân biệt và t₁t₂ > 0

Chú ý: Khi thay đường thẳng d bằng trục Ox, Oy hoặc đường tròn thì vẫn áp dụng kết quả trên. Với các điều kiện khác thì tuỳ từng trường hợp.

b, Hàm trùng phương $y=a{x}^4+b{x}^2+c$ . Khi đó:

- Xét trường hợp có ba cực trị $\to$ toạ độ các điểm cực trị

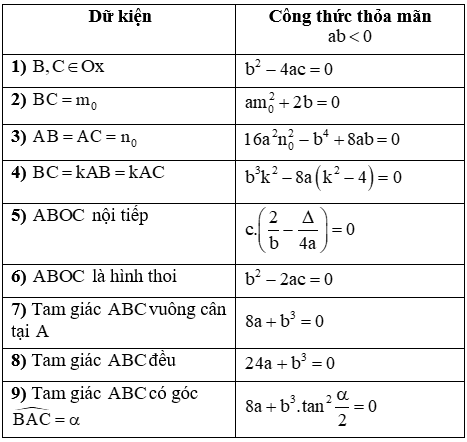
+ Đồ thị hàm số $y=a{x}^4+b{x}^2+c$ cắt trục hoành tại  điểm lập thành một cấp số cộng thì điều kiện là $\left\{\begin{array}{l}ac>0\\ ab<0\\ b^2=\frac{100}{9}ac\end{array}\right..$

2. Ví dụ minh hoạ.

Ví dụ 1. (ĐỀ CHÍNH THỨC 2016 – 2017) Tìm giá trị thực của tham số m để đường thẳng $d:y=\left(2m-1\right)x+3+m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=x^3-3x^2+1$.

A. $m=-\frac{1}{2}.$

B. $m=\frac{3}{2}.$

C.$m=\frac{1}{4}.$

D. $m=\frac{3}{4}.$

Lời giải

Xét hàm $y=x^3-3x^2+1$, có:

$$\begin{gathered} y^{\text{'}}=3x^2-6x\stackrel{}{\to }{y}^{\text{'}}=0 \\ \iff \left[\begin{array}{l}x=0\to y\left(0\right)=1\\ x=2\to y\left(2\right)=-3\end{array}\right.. \end{gathered}$$

Suy ra $A\left(0;1\right),B\left(2;-3\right)$ là hai điểm cực trị của đồ thị hàm số.

Suy ra đường thẳng AB có một VTCP là $\overrightarrow{AB}=\left(2;-4\right)\stackrel{}{\to }$VTPT $\overrightarrow{n_{AB}}=\left(2;1\right).$

Đường thẳng $d:y=\left(2m-1\right)x+3+m$ có một VTCP là $\overrightarrow{n_d}=\left(2m-1;-1\right).$

Yêu cầu bài toán  $\iff \overrightarrow{n_{AB}}.\overrightarrow{n_d}=0$

$\iff 2.\left(2m-1\right)-1=0\iff m=\frac{3}{4}.$

Chọn D.

Ví dụ 2. Cho hàm số $y=\frac{1}{4}{x}^4-\left(3m+1\right)x^2+2\left(m+1\right)$ với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ.

A. $m=-\frac{2}{3}$

B. $m=\frac{2}{3}$

C. $m=-\frac{1}{3}$

D. $m=\frac{1}{3}$.

Lời giải

Ta có

Chọn D.

Cách áp dụng công thức giải nhanh: Điều kiện để có ba cực trị $ab<0\iff m>-\frac{1}{3}.$

Yêu cầu bài toán:

$$\begin{gathered} G\equiv O\stackrel{}{\to }{b}^2-6ac=0 \\ \iff {\left(3m+1\right)}^2-6.\frac{1}{4}.2\left(m+1\right)=0 \\ \iff \left[\begin{array}{l}m=\frac{1}{3}\left(tm\right)\\ m=-\frac{2}{3}\left(loai\right)\end{array}\right.. \end{gathered}$$

3. Bài tập tự luyện.

Câu 1. Tìm m để đồ thị hàm số $y=x^4-2\left(m^2-m+1\right)x^2+m-1$ có một điểm cực đại, hai điểm cực tiểu và thỏa mãn khoảng cách giữa hai điểm cực tiểu ngắn nhất.

A. $m=-\frac{1}{2}$

B. $m=\frac{1}{2}$

C. $m=\frac{3}{2}$

D. $m=-\frac{3}{2}$.

Câu 2. Cho hàm số $y=-x^4+2m{x}^2-4$ có đồ thị là (C_m). Tìm các giá trị của m để tất cả các điểm cực trị của (C_m) đều nằm trên các trục tọa độ.

A. $m\le 0$

B. $m=2$

C. $m>0$

D. $m\le 0$ hoặc $m=2$.

Câu 3. Giá trị của tham số m bằng bao nhiêu để đồ thị hàm số $y=x^4-2m{x}^2+1$ có ba điểm cực trị A(0;1), B, C thỏa mãn BC = 4?

A. $m=\pm 4$

B. $m=\sqrt{2}$

C. $m=4$

D. $m=\pm \sqrt{2}$

Câu 4. Cho hàm số $y=x^4-2\left(m+1\right)x^2+m^2$, với m là tham số thực. Tìm m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.

A. m = -1

B. m = -0

C. m = 1

D. Đáp án khác.

Câu 5. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y=x^4+2m{x}^2+1$ có ba điểm cực trị tạo thành tam giác vuông cân.

A. $m=-\frac{1}{\sqrt[3]{9}}$

B. m = - 1

C. $m=\frac{1}{\sqrt[3]{9}}$

D. m = 1.

Câu 6. Tìm m để đồ thị hàm số $y=\frac{1}{4}{x}^4-\left(3m+1\right)x^2+2\left(m+1\right)$ có ba điểm cực trị tạo thành tam giác có trọng tâm là gốc tọa độ.

A. $m=-\frac{2}{3}$

B. $m=\frac{2}{3}$

C. $m=-\frac{1}{3}$

D. $m=\frac{1}{3}$

Câu 7. (ĐỀ THPT QG 2017)  Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=x^4-2m{x}^2$ có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

A. $m>0$

B. $m<1$

C. $0<m<\sqrt[3]{4}$

D. $0<m<1$

Câu 8. Tìm tất cả các giá trị của tham số m để hàm số $f\left(x\right)=2x^3-3x^2-m$ có các giá trị cực trị trái dấu:

A. – 1 và 0.

B. (-∞;0) và (-1;+ ∞).

C. (-1;0).

D. [0;1].

Câu 9. Cho hàm số $y=2x^3-3\left(m+1\right)x^2+6mx+m^3$. Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho độ dài AB = $\sqrt{2}$.

A. m = 0.

B. m = 0 hoặc m = 2

C. m = 1.

D. m = 2.

Câu 10. Gọi x₁, x₂ là hai điểm cực trị của hàm số $y=x^3-3m{x}^2+3\left(m^2-1\right)x-m^3+m$. Giá trị của m để $x_1^2+x_2^2-x_1{x}_2=7$ là:

A. $m=0$

B. $m=\pm \frac{9}{2}$

C. $m=\pm \frac{1}{2}$

D. $m=\pm 2$

Câu 11. (ĐỀ THPT QG 2017) Tìm giá trị thực của tham số m để đường thẳng $d:y=(2m-1)x+3+m$ vuông góc với đường thẳng đi qua hai điểm cực trị của hàm số $y=x^3-3x^2+1$.

A. $m=\frac{3}{2}$

B. $m=\frac{3}{4}$

C. $m=-\frac{1}{2}$

D. $m=\frac{1}{4}$

Câu 12. (ĐỀ THPT QG 2017)  Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x³ – 3mx² + 4m³  có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ.

A. $m=-\frac{1}{\sqrt[4]{2}};m=\frac{1}{\sqrt[4]{2}}$

B. $m=-1,m=1$

C.  $m=1$

D. $m\ne 0$

Câu 13. Nếu x = 1 là hoành độ trung điểm của đoạn thẳng nối hai điểm cực đại, cực tiểu của đồ thị hàm số $y=\frac{1}{3}{x}^3-\left(m+2\right)x^2+\left(2m+3\right)x+2017$ thì tập tất cả các giá trị của m là:

A. m = -1.

B. m ≠ -1.

C. $m=-\frac{3}{2}$

D. Không có giá trị m.

Câu 14. Giá trị của m để khoảng cách từ điểm M(0;3) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=x^3+3mx+1$ bằng $\frac{2}{\sqrt{5}}$ là:

A. $\left[\begin{array}{l}m=1\\ m=-1\end{array}\right.$

B. $m=-1$.            

C. $\left[\begin{array}{l}m=-1\\ m=3\end{array}\right.$

D. Không tồn tại m.

Câu 15. Cho hàm số $y=2x^3+3\left(m-1\right)x^2+6\left(m-2\right)x-1$. Xác định m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2;3).

A. $m\in \left(-1;3\right)\cup \left(3;4\right)$

B. $m\in \left(1;3\right)$

C. $m\in \left(3;4\right)$

D. $m\in \left(-1;4\right)$.

Câu 16. Để hàm số $y=x^3+6x^2+3\left(m+2\right)x-m-6$ có cực đại, cực tiểu tại $x_1,x_2$ sao cho $x_1<-1<x_2$ thì giá trị của m là:

A. $m>1$

B. $m<1$

C. $m>-1$

D. $m<-1$.

Câu 17. Tìm tất cả các giá trị của tham số m để hàm số $y=\frac{1}{3}{x}^3-m{x}^2+\left(m+2\right)x$ có hai điểm cực trị nằm trong khoảng (0;+∞)?

A. m > 2.

B. m < 2.

C. m = 2.

D. 0 < m < 2.

Câu 18. Với các giá trị nào của m thì hàm số $y=x^3-3x^2+3mx+1$ có các điểm cực trị nhỏ hơn 2?

A. $m>0$

B. $m<1$

C. $\left[\begin{array}{l}m<0\\ m>1\end{array}\right.$

D. $0<m<1$.

Câu 19. Cho hàm số $y=2x^3-3\left(2a+1\right)x^2+6a\left(a+1\right)x+2$. Nếu gọi x₁, x₂ lần lượt là hoành độ các điểm cực trị của đồ thị hàm số thì giá trị |x₁ – x₂| bằng:

A. a + 1.

B. a.

C. a – 1.

D. 1.

Câu 20. Cho hàm số $y=2x^3+m{x}^2-12x-13$. Với giá trị nào của m thì đồ thị hàm số có điểm cực đại, cực tiểu cách đều trục tung ?

A. 2.

B. - 1.

C. 1.

D. 0.

Câu 21. Đồ thị hàm số $y=-x^3+3m{x}^2-3m-1$ có hai điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng $d:x+8y-74=0$ thì tập tất cả các giá trị của m:

A. $m=1$

B. $m=-2$

C. $m=-1$

D. $m=2$

Câu 22. Cho hàm số $y=x^3+3x^2+mx+m-2$ với m là tham số, có đồ thị là $\left(C_m\right)$. Xác định m để (C_m) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành ?

A. $m<2$.

B. $m\le 3$

C. $m<3$

D. $m\le 2$

Câu 23. Cho hàm số $y=\frac{1}{3}{x}^3-m{x}^2+\left(2m-1\right)x-3$ với m là tham số, có đồ thị là (C_m). Xác định m để (C_m) có các điểm cực đại và cực tiểu nằm về cùng một phía đối với trục tung ?

A. $m\le \frac{1}{2}$

B. $m>1$

C. $\left\{\begin{array}{l}m>\frac{1}{2}\\ m\ne 1\end{array}\right.$

D. $\left\{\begin{array}{l}m>1\\ m\ne \frac{1}{2}\end{array}\right.$

Câu 24. Hàm số $y=a{x}^3+b{x}^2+cx+d$ đạt cực trị tại x₁, x₂ nằm hai phía trục tung khi và chỉ khi:

A. $a>0,b<0,c>0$

B. a và c trái dấu.

C. $b^2-12ac\ge 0$

D. $b^2-12ac>0$.

Câu 25. Cho hàm số $y=x^3-3m{x}^2+4m^2-2$. Tìm m để đồ thị hàm số có hai điểm cực trị A, B sao cho I(1;0) là trung điểm của AB.

A. $m=0$

B. $m=-1$

C. $m=1$

D. $m=2$

Câu 26. Với giá trị nào của tham số m thì đồ thị hàm số$y=x^3-3m{x}^2+2$  có hai điểm cực trị A, B sao cho A, B và M(1;-2) thẳng hàng.

A. $m=0$

B. $m=\sqrt{2}$

C. $m=-\sqrt{2}$

D. $m=\pm \sqrt{2}$

Câu 27. Với giá trị nào của tham số m thì đồ thị hàm số $y=-x^3+3mx+1$ có hai điểm cực trị A, B sao cho tam giác OAB vuông tại O, với O là gốc tọa độ ?

A. $m=-1.$

B. $m>0.$

C. $m=\frac{1}{2}.$

D.  $m=0.$

Câu 28. Cho hàm số $y=x^3-3x^2-mx+2$ với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng $d:x+4y-5=0$ một góc $\alpha ={45}^0.$

A. $m=-\frac{1}{2}.$

B. $m=\frac{1}{2}.$

C.  $m=0$

D. $m=\frac{\sqrt{2}}{2}.$

Câu 29. Cho hàm số $y=x^4-2m{x}^2+2$ với m là tham số thực. Có bao nhiêu giá trị nguyên của  để đồ thị hàm số có ba điểm cực trị $A,B,C$ thỏa mãn $OA.OB.OC=12$ với O là gốc toạ độ?

A. 2

B. 1

C. 0

D. 4

Câu 30. Cho hàm số $y=-x^4+2m{x}^2-4$ có đồ thị là $\left(C_m\right)$. Tìm tất cả các giá trị thực của tham số m để tất cả các điểm cực trị của $\left(C_m\right)$ đều nằm trên các trục tọa độ.

A. $m=\pm 2$

B. $m=2$

C. $m>0$

D. $m=-2$, $m>0$.

Câu 31. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=x^4-2m{x}^2+1$ có ba điểm cực trị A(0;1), B, C thỏa mãn BC=4.

A. $m=\pm 4$

B. $m=\sqrt{2}$

C. $m=4$

D. $m=\pm \sqrt{2}$.

Câu 32. Cho hàm số $y=x^4-2\left(m+1\right)x^2+m^2$ với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.

A. $m=-1$

B. $m=0$

C. $m=1$

D. $m>-1$.

Câu 33. (ĐỀ MINH HỌA 2016 – 2017) Tìm giá trị thực của tham số m sao cho đồ thị của hàm số $y=x^4+2m{x}^2+1$ có ba điểm cực trị tạo thành tam giác vuông cân.

A. $m=-\frac{1}{\sqrt[3]{9}}$

B. $m=-1$

C. $m=\frac{1}{\sqrt[3]{9}}$

D. $m=1$.

Câu 34. Cho hàm số $y=3x^4+2\left(m-2018\right)x^2+2017$ với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng ${120}^0$.

A. $m=-2018.$

B. $m=-2017$

C. $m=2017$

D. $m=2018.$

Câu 35. (ĐỀ CHÍNH THỨC 2016 – 2017) Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số $y=x^4-2m{x}^2$ có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

A. $m>0.$

B. $m<1.$

C. $0<m<\sqrt[3]{4}.$

D. $0<m<1.$

Câu 36. Cho hàm số $y=x^4-m{x}^2+m-2$ với m là tham số thực. Tìm giá trị của  để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn nội tiếp bằng 1.

A. $m=-2.$

B. $m=1.$

C. $m=2.$

D. $m=4$

Đáp án