Các công thức nguyên hàm cơ bản đầy đủ, chi tiết nhất - Toán lớp 12

1. Lý thuyết

a) Định nghĩa:

Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi $x\in K$.

Định lí:

1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó $F\left(x\right)+C,C\in ℝ$ là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu $\int f\left(x\right)d\text{x}=F\left(x\right)+C$.

b) Tính chất của nguyên hàm

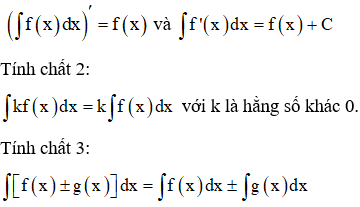
c) Sự tồn tại của nguyên hàm

Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

d. Bảng nguyên hàm của một số hàm số sơ cấp

Nhận xét. Khi thay x bằng (ax + b) thì lấy nguyên hàm nhân kết quả thêm $\frac{1}{a}\cdot$

2. Ví dụ minh họa

Ví dụ 1: Tính nguyên hàm của các hàm số sau:

a) f(x)= x³ + 3x + 2

b) $y=x^2-3x+\frac{1}{x}+\frac{1}{\sqrt[3]{x^2}}$

c) f(x) = (x + 1)(x + 2)

d) $f\left(x\right)=\frac{2}{5-2x}+\frac{2}{x}+\frac{3}{x^2}$

Lời giải

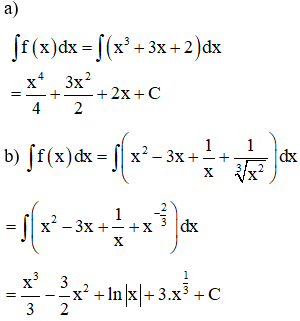
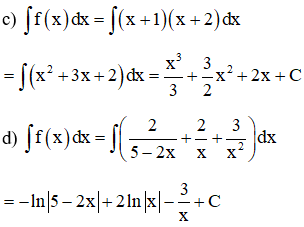
Ví dụ 2: Tính các nguyên hàm

a) $\int \left(\frac{1}{{\cos }^{2}x}+x^4\right)dx$

b) $\int \left(3\cos x-3^{x-1}\right)dx$

c) $\int \left(\frac{1}{x}-e^{x+1}\right)dx$

Lời giải

a) 

$$\begin{gathered} \int \left(\frac{1}{{\cos }^{2}x}+x^4\right)dx \\ =\int \frac{1}{{\cos }^{2}x}dx+\int x^{4}dx=\tan x+\frac{x^5}{5}+C \end{gathered}$$

b)

$$\begin{gathered} \int \left(3\cos x-3^{x-1}\right)dx \\ =\int 3\cos xdx-\int 3^{x-1}dx \\ =3\sin x-\frac{3^{x-1}}{\ln 3}+C \end{gathered}$$

c)

$$\begin{gathered} \int \left(\frac{1}{x}-e^{x+1}\right)dx \\ =\int \frac{1}{x}dx-\int e^{x-1}dx \\ =\ln \left|x\right|-e^{x-1}+C \end{gathered}$$