Công thức giải phương trình lôgarit chi tiết nhất - Toán lớp 12

1. Định nghĩa

- Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.

- Phương trình lôgarit cơ bản có dạng: ${\log }_{a}x=b\left(a>0,a\ne 1\right)$

Theo định nghĩa lôgarit ta có: ${\log }_{a}x=b\iff x=a^b$

Minh họa bằng đồ thị

Ta vẽ đồ thị hàm số $y={\log }_{a}x$ và đường thẳng $y=b$ trên cùng một hệ trục tọa độ

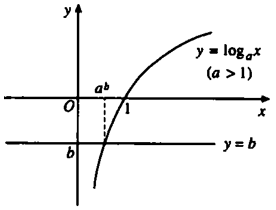
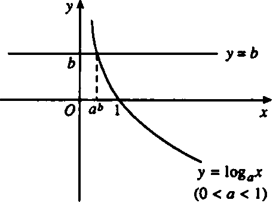
Dựa vào đồ thị ta thấy: Trong cả hai trường hợp thì đường thẳng $y=b$ luôn cắt nhau tại một điểm với mọi $b\in ℝ$.

Vậy ta có kết luận sau:

Phương trình ${\log }_{a}x=b\left(a>0,a\ne 1\right)$ luôn có nghiệm duy nhất $x=a^b\forall b$

- Chú ý: Khi giải một phương trình lôgarit ta cần tìm điều kiện của x

2. Cách giải một số phương trình lôgarit đơn giản

a. Đưa về cùng cơ số

- Áp dụng một số tính chất của lôgarit:

$$\begin{gathered} {\log }_a\left(x.y\right)={\log }_{a}x+{\log }_{a}y \\ {\log }_a\frac{x}{y}={\log }_{a}x-{\log }_{a}y \\ {\log }_a{b}^{\alpha }=\alpha .{\log }_{a}b \\ {\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a} \\ {\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b\left(\alpha \ne 0\right) \end{gathered}$$            

VD1. Giải các phương trình sau:

a. ${\log }_{3}x+{\log }_{9}x=6$

b. ${\log }_{2}x+{\log }_{4}x+{\log }_{8}x=11$

c. $\ln \left(2x^2-x\right)-\ln x=\ln 3$

Lời giải:

a. ${\log }_{3}x+{\log }_{9}x=6$. Điều kiện $x>0$

Phương trình

$$\begin{gathered} \iff {\log }_{3}x+\frac{1}{2}{\log }_{3}x=6 \\ \iff {\log }_{3}x=4\iff x=3^4 \end{gathered}$$

$\iff x=81$(Thỏa mãn)

Vậy phương trình đã cho có nghiệm là $x=81$

b. ${\log }_{2}x+{\log }_{4}x+{\log }_{8}x=11$. Điều kiện $x>0$

Phương trình

$$\begin{gathered} \iff {\log }_{2}x+\frac{1}{2}{\log }_{2}x+\frac{1}{3}{\log }_{2}x=11 \\ \iff \frac{11}{6}{\log }_{2}x=11 \\ \iff {\log }_{2}x=6\iff x=2^6\iff x=64 \end{gathered}$$

Vậy phương trình đã cho có nghiệm là x = 64

c. $\ln \left(2x^2-x\right)-\ln x=\ln 3$.

Điều kiện $x>\frac{1}{2}$

Phương trình

$$\begin{gathered} \iff \ln \frac{2x^2-x}{x}=\ln 3 \\ \begin{array}{l}\iff \frac{2x^2-x}{x}=3\\ \iff 2x^2-x=3x\\ \iff 2x^2-4x=0\iff \left[\begin{array}{l}x=0\\ x=2\end{array}\right.\left(L\right)\\ \iff x=2\end{array} \end{gathered}$$

Vậy phương trình đã cho có nghiệm $x=2$

b. Đặt ẩn phụ

VD2. Giải các phương trình sau

a. ${\log }_{{}_2}^{2}x-3{\log }_{2}x+2=0$

b. $\frac{1}{3-\log x}+\frac{3}{1+\log x}=2$

c. $1+2{\log }_{x+2}5={\log }_5\left(x+2\right)$

Lời giải:

a.

b.

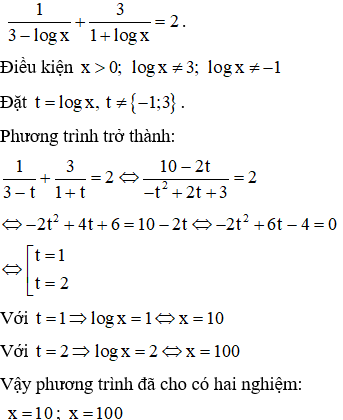
c. 

c. Mũ hóa.

VD3. Giải các phương trình sau:

a. ${\log }_2\left(5-2^x\right)=2-x$

b. ${\log }_3\left(2-9^x\right)=x$

c. $x^{\log 9}+9^{\log x}=6$

Lời giải:

a.

b.

c.

d. Đánh giá hàm số

VD4. Giải các phương trình sau:

a. ${\log }_{3}x=-x+11$

b. ${\log }_2\left(1+\sqrt{x}\right)={\log }_{3}x$

Lời giải:

a.

b.

${\log }_2\left(1+\sqrt{x}\right)={\log }_{3}x$

Điều kiện x >0

Đặt ${\log }_2\left(1+\sqrt{x}\right)={\log }_{3}x=t$

$\Rightarrow \left\{\begin{array}{l}1+\sqrt{x}=2^t\\ x=3^t\end{array}\right.\iff \left\{\begin{array}{l}x={\left(2^t-1\right)}^2\\ x=3^t\end{array}\right.$

Ta được phương trình:

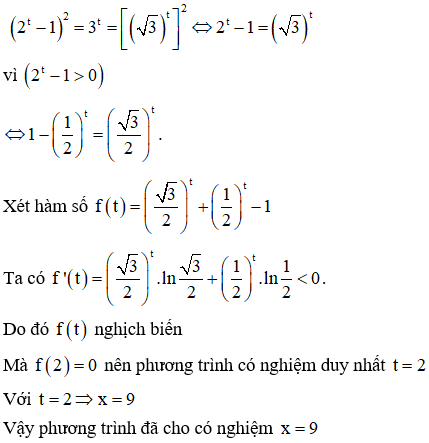
3. Luyện tập

Bài 1. Giải các phương trình sau:

a. ${\log }_3\left(5x+3\right)={\log }_3\left(7x+5\right)$

b. $\log \left(x-1\right)-\log \left(2x-11\right)=\log 2$

c. $\log \left(x^2-6x+7\right)=\log \left(x-3\right)$

Bài 2. Giải các phương trình sau:

a. $\frac{1}{2}\log \left(x^2+x-5\right)=\log 5x+\log \frac{1}{5x}$

b. ${\log }_{\sqrt{2}}x+4{\log }_{4}x+{\log }_{8}x=13$

c. ${\log }_4\left[\left(x+2\right)\left(x+3\right)\right]+{\log }_4\frac{x-2}{x+3}=2$

Bài 3. Giải các phương trình sau:

a. ${\log }_2\left(2^x+1\right).{\log }_2\left(2^{x+1}+2\right)=2$

b. $x^{3{\log }^{3}x-\frac{2}{3}\log x}=100.\sqrt[3]{10}$

Bài 4. Giải các phương trình sau:

a. ${\log }_{\frac{1}{3}}x=3x$

b. ${\log }_{4}x=\frac{4}{x}$

c. ${16}^x={\log }_{\frac{1}{2}}x$