Nguyên hàm và cách giải bài tập cơ bản - Toán lớp 12
Hamchoi.vn giới thiệu 50 Nguyên hàm và cách giải bài tập cơ bản - Toán lớp 12 lớp 12 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm. Bên cạnh có là 29 bài tập vận dụng để học sinh ôn luyện dạng Toán 12 này.
Nguyên hàm và cách giải bài tập cơ bản - Toán lớp 12
A. LÝ THUYẾT.
1. Khái niệm nguyên hàm.
- Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu với mọi x thuộc K.
, x K
Định lí:
1) Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng , với C là một hằng số.
Do đó là họ tất cả các nguyên hàm của f(x) trên K.
- Nếu F(x) có đạo hàm thì:
- với k là hằng số khác 0.
-
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm các hàm số thường gặp.




B. CÁC DẠNG BÀI TOÁN HAY GẶP VÀ VÍ DỤ.
Phương pháp giải: Áp dụng các công thức nguyên hàm cơ bản đã nêu ở phần lý thuyết để giải các bài toán sau.
Bài toán 1: Tìm nguyên hàm F(x) của hàm số f(x) trên .
Ví dụ 1. Cho hàm số . Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Lời giải
Chọn B.
Bài toán 2: Tìm F(x) là một nguyên hàm của hàm f(x) trên .
Ví dụ 2. Cho . Hỏi F(x) là nguyên hàm của hàm số nào dưới đây?
A.
B.
C.
D.
Lời giải
Ta có:
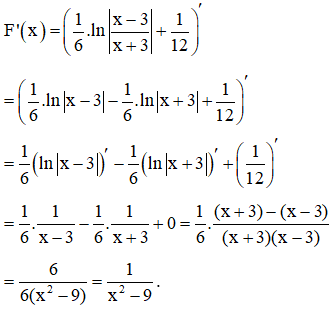
Chọn A.
Bài toán 3: Xác định nguyên hàm của một hàm số với điều kiện cho trước.
Ví dụ 3. Cho hàm số f(x) thỏa mãn và . Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Lời giải
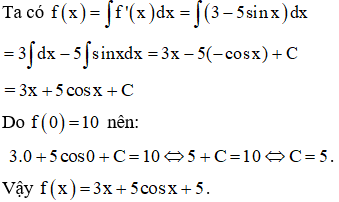
Chọn A.
Bài toán 4: Tìm giá trị của tham số để F(x) là một nguyên hàm của f(x).
Ví dụ 4. Cho kết quả của có dạng , trong đó a, b là hai số hữu tỉ. Giá trị a bằng:
A. 2 .
B. 1 .
C. 9 .
D. 32 .
Lời giải
Theo đề, ta cần tìm . Sau đó, ta xác định giá trị của a.
Ta có:
Suy ra để có dạng thì a = 1, b = 2.
Chọn B.
C. BÀI TẬP TỰ LUYỆN.
Câu 1. Nguyên hàm của hàm số là
A.
B.
C.
D.
Câu 2. Nguyên hàm của là:
A.
B.
C.
D.
Câu 3. Nguyên hàm của là:
A.
B.
C.
D.
Câu 4. Hàm số có nguyên hàm trên K nếu:
A. xác định trên K.
B. có giá trị lớn nhất trên K
C. có giá trị nhỏ nhất trên K
D. liên tục trên K
Câu 5. Mệnh đề nào sau đây sai?
A. Nếu là một nguyên hàm của trên và C là hằng số thì .
B. Mọi hàm số liên tục trên đều có nguyên hàm trên .
C. là một nguyên hàm của trên
D.
Câu 6. Gọi là nguyên hàm của hàm số , với m là tham số thực. Tìm một nguyên hàm của biết rằng và .
A.
B. .
C. .
D. Đáp án A và B.
Câu 7. Họ nguyên hàm của là:
A. .
B. .
C. .
D. .
Câu 8. Cho , trong đó a,b là hai số hữu tỉ. Biết rằng . Giá trị a,b lần lượt bằng:
A. .
B.
C.
D. 2; 4.
Câu 9. Tính
A.
B.
C.
D.
Câu 10. Nguyên hàm của hàm số là
A.
B.
C.
D.
Câu 11. Nguyên hàm của hàm số trên là:
A.
B.
C.
D.
Câu 12. Hàm số là một nguyên hàm của hàm số nào sau đây ?
A.
B.
C.
D.
Câu 13. Tính
A.
B.
C.
D.
Câu 14. Tính
A.
B.
C.
D.
Câu 15. Tính .
A.
B.
C.
D.
Câu 16. Tìm một nguyên hàm F(x) của biết F(1) = 0.
A.
B.
C.
D.
Câu 17. Tìm hàm số F(x) biết rằng F’(x) = 4x3 – 3x2 + 2 và F(-1) = 3.
A.
B.
C.
D.
Câu 18. Họ nguyên hàm của hàm số là :
A.
B.
C.
D.
Câu 19. Họ nguyên hàm của hàm số là :
A.
B.
C.
D.
Câu 20. Họ nguyên hàm của hàm số là :
A.
B.
C.
D.
Câu 21. Họ nguyên hàm của hàm số là :
A.
B.
C.
D.
Câu 22. Nguyên hàm của hàm số là hàm số
nào trong các hàm số sau?
A.
B.
C.
D.
Câu 23. Nguyên hàm của hàm số thỏa mãn điều kiện là:
A.
B.
C.
D. Đáp án khác.
Câu 24. Biết F(x) là nguyên hàm của hàm số và F(2) = 1. Khi đó F(3) bằng bao nhiêu:
A.
B.
C.
D.
Câu 25. Hàm số có nguyên hàm trên K nếu
A. xác định trên K
B. có giá trị lớn nhất trên K
C. có giá trị nhỏ nhất trên K
D. liên tục trên K
Câu 26. Cho hai hàm số là hàm số liên tục, có lần lượt là nguyên hàm của . Xét các mệnh đề sau:
(I): là một nguyên hàm của
(II): là một nguyên hàm của
(III): là một nguyên hàm của
Mệnh đề nào là mệnh đề đúng ?
A. I
B. I và II
C. I, II, III
D. II
Câu 27. Trong các khẳng định sau khẳng định nào sai?
A. ( là hằng số)
B. ( là hằng số)
C. ( là hằng số)
D. ( là hằng số)
Câu 28. bằng:
A.
B.
C.
D.
Câu 29. Trong các khẳng định sau, khẳng định nào sai?
A. là một nguyên hàm của .
B. là một nguyên hàm của .
C. Nếu và đều là nguyên hàm của hàm số thì (hằng số).
D.
Đáp án
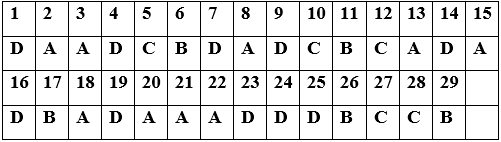
Bài viết liên quan
- Công thức giải bất phương trình lôgarit chi tiết nhất - Toán lớp 12
- Công thức tính trả góp vay vốn chi tiết nhất - Toán lớp 12
- Các phương pháp tính nguyên hàm và cách giải bài tập - Toán lớp 12
- Nguyên hàm của hàm số phân thức hữu tỉ và cách giải - Toán lớp 12
- Nguyên hàm của hàm số lượng giác và cách giải - Toán lớp 12
