Bài toán về cực trị tọa độ không gian và cách giải - Toán lớp 12
Hamchoi.vn giới thiệu 50 Bài toán về cực trị tọa độ không gian và cách giải - Toán lớp 12 lớp 12 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm. Bên cạnh có là 10 bài tập vận dụng để học sinh ôn luyện dạng Toán 12 này.
Bài toán về cực trị tọa độ không gian và cách giải - Toán lớp 12
I. LÝ THUYẾT
Với bài toán cực trị trong không gian Oxyz chúng ta thường xử lí theo một trong hai hướng sau:
Hướng 1: Đại số: Chuyển đại lượng cần tìm min, max về một biểu thức đại số và dùng các bất đẳng thức hoặc khảo sát hàm số để tìm min, max.
Hướng 2: Hình học: Với hướng này ta sử dụng các bất đẳng thức để đánh giá.
II. PHƯƠNG PHÁP GIẢI
Bài toán 1: Trong không gian Oxyz cho các điểm và mặt phẳng (P): ax + by + cz + d = 0. Tìm điểm sao cho
1. MA + MB nhỏ nhất.
2. |MA – MB| lớn nhất với .
Phương pháp:
+) Xét vị trí tương đối của các điểm A, B so với mặt phẳng (P).
+) Nếu:
thì hai điểm A, B cùng phía với mặt phẳng (P).
+) Nếu:
thì hai điểm A, B nằm khác phía với mặt phẳng (P).
1. MA + MB nhỏ nhất.
+) Trường hợp 1: Hai điểm A, B ở khác phía so với mặt phẳng (P)
Vì A, B ở khác phía so với mặt phẳng (P) nên MA + MB nhỏ nhất bằng AB khi và chỉ khi .
+) Trường hợp 2: Hai điểm A, B ở cùng phía so với mặt phẳng (P).
Gọi A’ đối xứng với A qua mặt phẳng (P) khi đó A’ và B ở khác phía (P) và MA MA’ nên
Vậy MA + MB nhỏ nhất bằng A’B khi
2. |MA – MB| lớn nhất.
+) Trường hợp 1: Hai điểm A, B ở cùng phía so với mặt phẳng (P).
Vì A, B ở cùng phía so với mặt phẳng (P) nên |MA – MB| lớn nhất bằng AB khi và chỉ khi .
+) Trường hợp 2: Hai điểm A, B ở khác phía so với mặt phẳng (P).
Gọi A’ đối xứng với A qua mặt phẳng (P), khi đó A’ và B ở cùng phía (P) và
MA = MA’ nên
Vậy |MA – MB| lớn nhất bằng A’B khi .
Bài toán 2: Lập phương trình mặt phẳng (P) biết
1. (P) đi qua đường thẳng và khoảng cách từ đến (P) lớn nhất.
2. (P) đi qua và tạo với mặt phẳng (Q) một góc nhỏ nhất.
3. (P) đi qua và tạo với đường thẳng d một góc lớn nhất.
Phương pháp:
Cách 1: Dùng phương pháp đại số
1. Giả sử đường thẳng
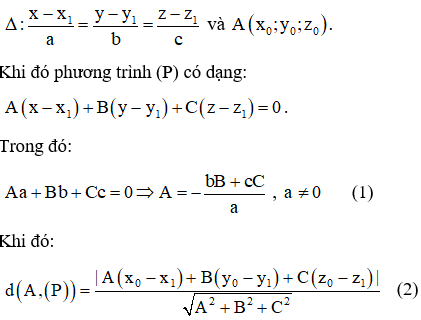
Thay (1) vào (2) và đặt , ta đươc .
Trong đó , khảo sát hàm ta tìm được max f(t). Từ đó suy ra được sự biểu diễn của A, B qua C rồi cho C giá trị bất kì ta tìm được A, B.
2. và 3. làm tương tự
Cách 2: Dùng hình học
1. Gọi K, H lần lượt là hình chiếu của A lên và (P), khi đó ta có:
, mà AK không đổi. Do đó d (A, (P)) lớn nhất .
Hay (P) là mặt phẳng đi qua K, nhận làm vectơ pháp tuyến.
2. Nếu:
nên ta xét và (Q) không vuông góc với nhau.
+) Gọi (B) là một điểm nào đó thuộc , dựng đường thẳng qua B và vuông góc với (Q). Lấy điểm C cố định trên đường thẳng đó. Hạ . Góc giữa mặt phẳng (P) và mặt phẳng (Q) là .Ta có
Mà không đổi, nên nhỏ nhất khi .
+) Mặt phẳng (P) cần tìm là mặt phẳng chứa và vuông góc với mặt phẳng (BCK). Suy ra là VTPT của (P).
3. Gọi M là một điểm nào đó thuộc , dựng đường thẳng d’ qua M và song song với d. Lấy điểm A cố định trên đường thẳng đó. Hạ . Góc giữa mặt phẳng (P) và đường thẳng d’ là . Ta có
Mà không đổi, nên lớn nhất khi
+) Mặt phẳng (P) cần tìm là mặt phẳng chứa và vuông góc với mặt phẳng . Suy ra là VTPT của (P).
III. VÍ DỤ MINH HỌA
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz cho hai điểm A (1; 0; 2), B (0; -1; 2) và mặt phẳng (P): x + 2y – 2z + 12 = 0. Tìm tọa độ điểm M thuộc (P) sao cho MA + MB nhỏ nhất?
A. M (2; 2; 9)
B.
C.
D.
Hướng dẫn giải
Thay tọa độ A (1; 0; 2), B (0; -1; 2) vào phương trình mặt phẳng (P), ta được P(A).P(B) > 0 hai điểm A, B cùng phía với đối với mặt phẳng (P).
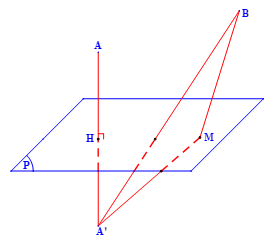
Gọi A’ là điểm đối xứng của A qua (P). Ta có
Nên min(MA + MB) = A’B khi và chỉ khi M là giao điểm của A’B với (P).
Phương trình (AA’ đi qua A (1; 0; 2) và có véctơ chỉ phương ).
Gọi H là giao điểm của AA’ trêN (P), suy ra tọa độ của H là H (0; -2; 4), suy ra A’ (-1; -4; 6), nên phương trình .
Vì M là giao điểm của A’B với (P) nên ta tính được tọa độ
Chọn D.
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz cho điểm E (8; 1; 1).Viết phương trình mặt phẳng qua E và cắt nửa trục dương Ox, Oy, Oz lần lượt tại A, B, C sao cho OG nhỏ nhất với G là trọng tâm tam giác ABC.
A. x + y + 2z – 11 = 0.
B. 8x + y + z – 66 = 0
C. 2x + y + z – 18 = 0.
D. x + 2y + 2z – 12 = 0.
Hướng dẫn giải
Gọi A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c > 0.
Theo đề bài ta có: . Cần tìm giá trị nhỏ nhất của .
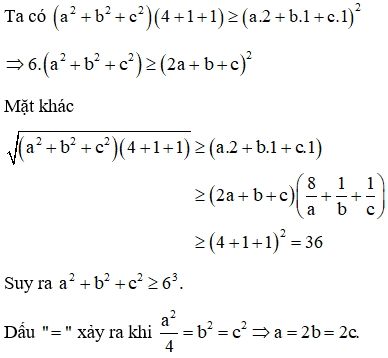
Vậy đạt giá trị nhỏ nhất bằng 216 khi a = 12, b = c = 6.
Vậy phương trình mặt phẳng là : hay x + 2y + 2z – 12 = 0.
Chọn D.
Ví dụ 3 : Trong không gian với hệ tọa độ Oxyz, cho điểm M (1; 2; 1). Mặt phẳng (P) thay đổi đi qua M lần lượt cắt các tia Ox, Oy, Oz tại A, B, C khác O. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC.
A. 54
B. 6
C. 9
D. 18
Hướng dẫn giải
Gọi A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c > 0.
Phương trình mặt phẳng

Chọn C.
IV. BÀI TẬP ÁP DỤNG
Câu 1: Trong không gian Oxyz, cho điểm và mặt cầu . Đường thẳng d thay đổi, đi qua điểm M, cắt mặt cầu (S) tại hai điểm A, B phân biệt. Tính diện tích lớn nhất S của tam giác OAB.
A.
B. S = 4.
C.
D.
Câu 2: Phương trình của mặt phẳng nào sau đây đi qua điểm M (1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất?
A. 6x + 3y + 2z + 18 = 0
B. 6x + 3y + 3z – 21 = 0
C. 6x + 3y + 3z + 21 = 0
D. 6x + 3y + 2z – 18 = 0
Câu 3: Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 3x + y – z + 5 = 0 và hai điểm A (1; 0; 2), B (2; -1; 4). Tìm tập hợp các điểm M (x; y; z) nằm trên mặt phẳng (P) sao cho tam giác MAB có diện tích nhỏ nhất.
A.
B.
C.
D.
Câu 4: Trong không gian với hệ tọa độ Oxyz, cho hai điểm M (-2; -2; 1), A (1; 2; -3) và đường thẳng . Tìm vectơ chỉ phương của đường thẳng đi qua M, vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất.
A.
B.
C.
D.
Câu 5 : Trong không gian với hệ toạ độ Oxyz, cho 4 điểm A (2; 4 ; -1), B (1; 4; -1), C (2; 4; 3), D (2; 2; -1). Biết M (x; y; z), để đạt giá trị nhỏ nhất thì x + y + z bằng
A. 7
B. 8
C. 9
D. 6
Câu 6 : Trong không gian với hệ trục toạ độ Oxyz, cho tứ diện ABCD có điểm A (1 ; 1 ; 1), B (2 ; 0 ; 2), C (-1 ; -1 ; 0), D (0 ; 3 ; 4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B’, C’, D’ thỏa mãn : . Viết phương trình mặt phẳng (B’C’D’) biết tứ diện AB’C’D’ có thể tích nhỏ nhất ?
A. 16x + 40y – 44z + 39 = 0
B. 16x + 40y + 44z – 39 = 0
C. 16x – 40y – 44z + 39 = 0
D. 16x – 40y – 44z – 39 = 0
Câu 7: Trong không gian với hệ tọa độ Oxyz gọi d đi qua điểm A (1; -1; 2), song song với (P): 2x – y – z + 3 = 0, đồng thời tạo với đường thẳng một góc lớn nhất. Phương trình đường thẳng d là
A.
B.
C.
D.
Câu 8: Trong không gian với hệ tọa độ Oxyz gọi d đi qua A (-1; 0; -1), cắt , sao cho góc giữa d và là nhỏ nhất. Phương trình đường thẳng d là
A.
B.
C.
D.
Câu 9: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (0; -2; -1), B (-2; -4; 3), C (1; 3; -1) và mặt phẳng (P): x + y – 2z – 3 = 0. Biết điểm thỏa mãn đạt giá trị nhỏ nhất. Tính S = a + b + c.
A. S = -2
B. S = 0
C. S = 1
D.
Câu 10: Trong không gian Oxyz, cho hai điểm A (2; 1; -2), B (-1; 0; 3), (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) lớn nhất. Khi đó khoảng cách từ gốc tọa độ đến (P) bằng
A.
B. 3
C. 1
D.
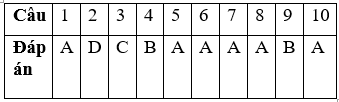
ĐÁP ÁN
Bài viết liên quan
- Các dạng toán về phương trình đường thẳng và cách giải - Toán lớp 12
- Các dạng toán về phương trình mặt cầu và cách giải - Lớp 12
- Bài toán về vị trí tương đối trong tọa độ không gian và cách giải - Toán lớp 12
- Các bài toán về góc trong không gian và cách giải - Toán lớp 12
- Các bài toán về khoảng cách trong không gian và cách giải - Toán lớp 12
