Các bài toán về khoảng cách trong không gian và cách giải - Toán lớp 12
Hamchoi.vn giới thiệu 50 Các bài toán về khoảng cách trong không gian và cách giải lớp 12 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm. Bên cạnh có là 10 bài tập vận dụng để học sinh ôn luyện dạng Toán 12 này.
Các bài toán về khoảng cách trong không gian và cách giải - Toán lớp 12
I. LÝ THUYẾT
1. Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng.
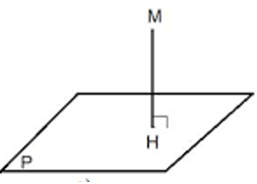
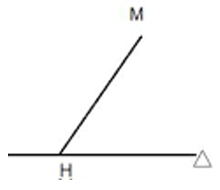
Khoảng cách từ một điểm M đến một mặt phẳng (P) (hoặc đến đường thẳng ∆) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P) (hoặc trên đường thẳng ∆).
+ Kí hiệu khoảng cách từ M đến (P) là d (M, (P))
+ Kí hiệu khoảng cách từ M đến ∆ là d (M, ∆)
2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.
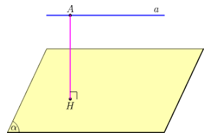
a) Khoảng cách giữa đường thẳng a và mặt phẳng song song với a là khoảng cách từ một điểm bất kì của a tới mặt phẳng cụ thể với A thuộc a.
Ta có: d(a, (α)) = d(A, (α)) = AH
với A thuộc a và H là hình chiếu của A lên mặt phẳng
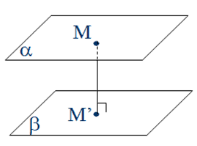
b) Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này tới mặt phẳng kia, cụ thể với M thuộc mặt phẳng .
3. Khoảng cách giữa hai đường thẳng chéo nhau
Đường thẳng MN cắt và vuông góc với cả a và b gọi là đường vuông góc chung của a và b.
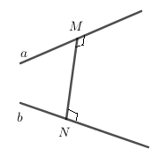
Khoảng cách giữa hai đường thẳng chéo nhau bằng độ dài đoạn vuông góc chung của hai đường thẳng chéo nhau đó. Cụ thể: d (a, b) = MN.
II. PHƯƠNG PHÁP GIẢI VÀ VÍ DỤ MINH HỌA
1. Khoảng cách từ một điểm đến mặt phẳng.
Phương pháp giải:
Khoảng cách từ đến mặt phẳng (P): Ax + By + Cz + D = 0 là:
Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x + 2y – 2z + 5 = 0 và điểm M (0; 2; 4). Tính d (M; (P)).
A.
B.
C.
D.
Hướng dẫn giải:
Ta có :
Chọn A.
2. Khoảng cách giữa hai mặt phẳng song song.
Phương pháp giải:
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia. Cụ thể, để tính khoảng cách giữa hai mặt phẳng song song (P) và (Q) ta thực hiện các bước như sau:
+) Lấy điểm M thuộc mặt phẳng (P).
+) Tính khoảng cách từ điểm M đến mặt phẳng (Q) (áp dụng công thức khoảng cách từ một điểm đến mặt phẳng).
Hướng dẫn giải:
Ví dụ 2: Khoảng cách giữa hai mặt phẳng song song (P): 4x – 3y + z – 2 = 0 và (Q): 12x – 9y + 3z + 1 = 0 là
A.
B. 1.
C.
D.
Hướng dẫn giải:
Lấy điểm
Chọn D.
3. Khoảng cách từ một điểm đến một đường thẳng
Phương pháp giải:
Khoảng cách từ điểm M đến một đường thẳng d đi qua điểm A có vectơ chỉ phương được xác định bởi công thức:
Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz khoảng cách từ điểm M (2; 0; 1) đến đường thẳng là
A.
B.
C.
D.
Hướng dẫn giải:
Đường thẳng d đi qua A (1; 0; 2) có một vectơ chỉ phương là .
Ta có:
Suy ra :
Khoảng cách từ điểm M (2; 0; 1) đến đường thẳng là:
Chọn C.
4. Khoảng cách giữa hai đường thẳng song song
Phương pháp giải:
Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia. Cụ thể, để tính khoảng cách giữa hai đường thẳng song song d và d’ ta thực hiện như sau:
+) Lấy M thuộc đường thẳng d.
+) Tính khoảng cách từ M đến đường thẳng d’ (bằng công thức khoảng cách từ một điểm đến một đường thẳng).
Ví dụ 4: Trong không gian Oxyz cho hai đường thẳng có phương trình lần lượt là
và . Tính khoảng cách giữa hai đường thẳng đó.
Hướng dẫn giải:
Ta lấy M (1; 2; 3) thuộc đường thẳng
Ta có đi qua A (3; 2; 5) và có một vectơ chỉ phương là .
Khi đó:
Vì song song nên ta có:
5. Khoảng cách giữa hai đường thẳng chéo nhau:
Phương pháp giải:
d đi qua điểm A và có vectơ chỉ phương và d’ đi qua điểm B và có vectơ chỉ phương là:
Ví dụ 5: Tính khoảng cách giữa hai đường thẳng chéo nhau và
A.
B.
C.
D.
Hướng dẫn giải:
Đường thẳng có vectơ chỉ phương là và đi qua điểm .
Đường thẳng có vectơ chỉ phương là và đi qua điểm .
Ta có:
,
Khoảng cách giữa hai đường thẳng và là
Chọn D.
6. Khoảng cách giữa đường thẳng d song song với mặt phẳng (P)
Phương pháp giải:
Khoảng cách giữa đường thẳng d song song với mặt phẳng (P) là khoảng cách từ một điểm M thuộc đường thẳng d đến mặt phẳng (P), cụ thể:
với (P): ax + by + cz + d = 0
Ví dụ 6: Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): x + 2y – 2z + 1 = 0. Khoảng cách giữa đường thẳng d và mặt phẳng (P) bằng
A.
B.
C.
D. 0
Hướng dẫn giải:
Đường thẳng d đi qua M (1; 0; -3) và nhận làm véc tơ chỉ phương.
Mặt phẳng (P) nhận làm véc tơ pháp tuyến.
Ta có:
Vậy :
Chọn B.
III. BÀI TẬP ÁP DỤNG
Câu 1: Trong không gian Oxyz, khoảng cách từ điểm A (1; 2; 2) đến mặt phẳng : x + 2y – 2z – 4 = 0 bằng:
A. 3
B. 1
C.
D.
Câu 2: Tính khoảng cách giữa hai mặt phẳng song song (P): 2x – y – 2z – 4 = 0 và (Q): 2x – y – 2z = 2 = 0.
A. 2
B. 6
C.
D.
Câu 3: Tính khoảng cách giữa mặt phẳng (P): 2x – y – 2z – 4 = 0 và đường thẳng d:
A.
B.
C. 0.
D. 2.
Câu 4: Khoảng cách từ điểm E (1; 1; 3) đến đường thẳng , bằng
A.
B.
C.
D. 0.
Câu 5: Trong không gian Oxyz khoảng cách từ điểm M (3; -4; 1) tới mặt phẳng (Oyz) bằng
A. 1.
B. 14.
C. 4
D. 3.
Câu 6: Tính khoảng cách h từ điểm A (2; 1; 4) đến đường thẳng
A.
B. h = 2.
C.
D. h = 5.
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + m = 0 và điểm A (1; 1; 1). Khi đó m nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng (P) bằng 1?
A. -2
B. -8
C. -2 hoặc - 8
D. 3.
Câu 8: Trong không gian Oxyz, khoảng cách từ điểm M (1; 3; 2) đến đường thẳng là
A.
B. 3.
C.
D. 2.
Câu 9: Khoảng cách giữa hai đường thẳng chéo nhau và là
A.
B.
C.
D.
Câu 10: Tính khoảng cách giữa hai đường thẳng chéo nhau và
A.
B.
C.
D.
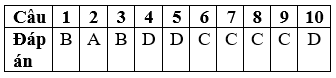
ĐÁP ÁN
Bài viết liên quan
- Các dạng toán về phương trình đường thẳng và cách giải - Toán lớp 12
- Các dạng toán về phương trình mặt cầu và cách giải - Lớp 12
- Bài toán về vị trí tương đối trong tọa độ không gian và cách giải - Toán lớp 12
- Các bài toán về góc trong không gian và cách giải - Toán lớp 12
- Bài toán về cực trị tọa độ không gian và cách giải - Toán lớp 12
