Công thức biện luận số nghiệm của phương trình dựa vào đồ thị chi tiết nhất - Toán lớp 12

1. Lí thuyết

Cho hai hàm số $y=f\left(x\right)$ có đồ thị $\left(C_1\right)$ và $y=g\left(x\right)$ có đồ thị $\left(C_2\right)$. Khi đó số nghiệm của phương trình $f\left(x\right)=g\left(x\right)$ sẽ bằng số giao điểm của $\left(C_1\right)$ và $\left(C_2\right)$

2. Áp dụng vào biện luận số nghiệm phương trình

Cho phương trình $f\left(x\right)=m$. Số nghiệm của phương trình đã cho phụ thuộc vào số giao điểm của đường thẳng $y=m$ với đồ thị hàm số $y=m$. Trong đó đường thẳng $y=m$ tịnh tiến trên trục Oy.

3. Cách biện luận số nghiệm phương trình $f\left(x\right)=m$

a. Cách 1: Khi bài toán cho sẵn đồ thị hàm số $y=f\left(x\right)$

- Ta dựa vào sự tịnh tiến của đường thẳng $y=m$ xem nó cắt đồ thị $y=f\left(x\right)$ tại mấy điểm, từ đó biện luận phương trình có 1 nghiệm; 2 nghiệm; ... hoặc vô nghiệm khi nào tùy thuộc vào khoảng giá trị của m.

 - Hình bên là đồ thị hàm số $y=x^3+3x^2-2$

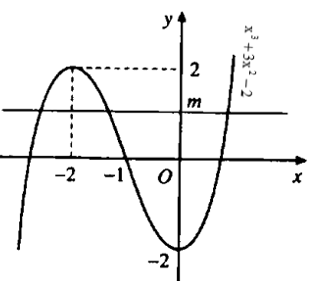
Ta biện luận số nghiệm của $x^3+3x^2-2=m$ như sau:

+ Phương trình có 1 nghiệm $\iff \left[\begin{array}{l}m>2\\ m<-2\end{array}\right.$

+ Phương trình có 2 nghiệm $m=\pm 2$

+ Phương trình có 3 nghiệm $\iff -2<m<2$

b. Cách 2: Khi bài toán không cho đồ thị

- Với cách này thì ta lập bảng biến thiên của hàm số $y=f\left(x\right)$

Sau đó ta biện luận tương tự như cách 1

- Cách này sẽ thuận tiện với những bài toán chưa có sẵn đồ thị

4. Ví dụ

VD1. Cho đồ thị hàm số $x^3-3x+m=0$ như hình bên.

a. Từ đồ thị hãy chỉ ra khoảng đồng biến, nghịch biến

b. Biện luận số nghiệm của phương trình $x^3-3x+m=0$

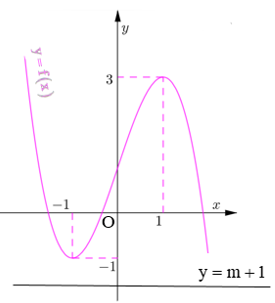
Lời giải:

a. Dựa vào đồ thị ta thấy

- Hàm số nghịch biến trên 2 khoảng $\left(-\infty ;-1\right)$ và $\left(1;+\infty \right)$

- Hàm số đồng biến trên trên khoảng $\left(-1;1\right)$

b. $x^3-3x+m=0$

$\iff -x^3+3x+1=m+1$(1)

Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị hàm số $y=f\left(x\right)$ và đường thẳng $y=m+1$

- Đường thẳng $y=m+1$ là đường thẳng song song với trục Ox. Tịnh tiến đường thẳng ta được:

+ phương trình (1) có 1 nghiệm: $\iff \left[\begin{array}{l}m+1>3\\ m+1<-1\end{array}\right.\iff \left[\begin{array}{l}m>2\\ m<-2\end{array}\right.$

+ phương trình (1) có 2 nghiệm $\iff m=\pm 2$

+ phương trình (1) có 3 nghiệm:

$$\begin{gathered} \iff -1<m+1<3 \\ \iff -2<m<2 \end{gathered}$$

VD2. Tìm m để phương trình $x^3+3x^2+2-m=0$ có 3 nghiệm thực phân biệt.

Lời giải:

$x^3+3x^2+2-m=0$

$\iff x^3+3x^2+2=m$(1)

- Số nghiệm của phương trình (1) bằng số giao điểm của $y=x^3+3x^2+2$ và $y=m$

- Xét hàm số $y=x^3+3x^2+2$ ta có:

$$\begin{gathered} y\text{'}=3x^2+6x=0 \\ \iff \left[\begin{array}{l}x=0\\ x=-2\end{array}\right. \end{gathered}$$

Bảng biến thiên:

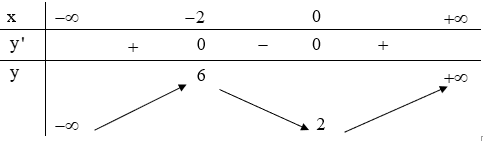
Dựa vào bảng biến thiên ta thấy, (1) có 3 nghiệm phân biệt $\iff 2<m<6$

5. Luyện tập

Bài 1.

Cho hàm số $y=-x^4+4x^2+2$ có đồ thị như hình bên.

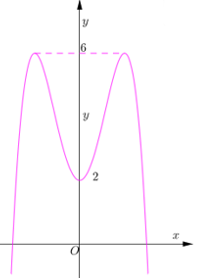
Biện luận số nghiệm của phương trình $x^4-4x^2+m-3=0$ theo m

Bài 2. Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như hình dưới.

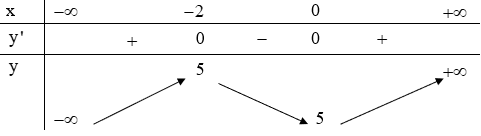
Biện luận số nghiệm của phương trình $2f\left(x\right)-m=0$

Bài 3.

Cho hàm số $y=f\left(x\right)$ liên tục trên $\left[-2;2\right]$ và có đồ thị là hình cong bên.

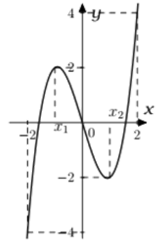
Số nghiệm của phương trình $\left|f\left(x\right)\right|=1$ trên đoạn $\left[-2;2\right]$ bằng?

Bài 4. Tìm m để phương trình $\left|x^2-4x+3\right|=m$ có 4 nghiệm phân biệt.

Bài 5. Tìm m để bất phương trình $x^3-3x^2+1-m<0$ nghiệm đúng với mọi $x\in \left[-1;1\right]$.