Công thức tính bán kính hình trụ chi tiết nhất - Toán lớp 12

1. Định nghĩa hình trụ tròn xoay

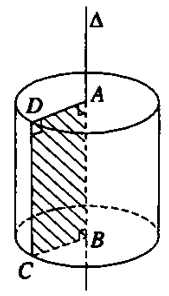
Ta xét hình chữ nhật ABCD. Khi quay hình đó xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh AB thì đường gấp khúc ADCB tạo thành một hình được gọi là hình trụ tròn xoay hay còn được gọi tắt là hình trụ.

Khi quay quanh AB, hai cạnh AD và BC sẽ vạch ra hai hình tròn bằng nhau gọi là hai đáy của hình trụ.

Độ dài đoạn CD gọi là độ dài đường sinh của hình trụ

Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh CD khi quay quanh AB gọi là mặt xung quanh của hình trụ.

Khoảng cách AB giữa hai mặt phẳng song song chứa hai đáy là chiều cao của hình trụ.

2. Công thức tính bán kính đáy của hình trụ

a. Công thức tính chu vi đường tròn; diện tích hình tròn

Đường tròn có chu vi $C=2\pi r\Rightarrow r=\frac{C}{2\pi }$

Hình tròn đáy có diện tích $S=\pi r^2\Rightarrow r=\sqrt{\frac{S}{\pi }}$

VD. Tính bán kính đáy của hình trụ trong các trường hợp sau:

a. Chu vi đường tròn đáy là $6\pi$

b. Diện tích đáy là $25\pi$

Lời giải:

a. Bán kính đường tròn đáy là $r=\frac{C}{2\pi }=\frac{6\pi }{2\pi }=3$

b. Bán kính đường tròn đáy là $r=\sqrt{\frac{S}{\pi }}=\sqrt{\frac{25\pi }{\pi }}=5$

b. Đáy là đường tròn ngoại tiếp đa giác

- Ngoại tiếp tam giác bất kì: 

$$\begin{gathered} R=\frac{abc}{4S} \\ =\frac{abc}{4\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}} \end{gathered}$$

Trong đó: a, b, c là độ dài 3 cạnh tam giác

p là nửa chu vi tam giác: $p=\frac{a+b+c}{2}$

- Ngoại tiếp tam giác vuông:$R=\frac{1}{2}.$cạnh huyền

Ngoại tiếp tam giác đều:

$R=\mathrm{canh}\cdot \frac{\sqrt{3}}{3}$

Ngoại tiếp hình vuông:

$\mathrm{R}=\mathrm{canh}\cdot \frac{\sqrt{2}}{2}$

VD1. Tính bán kính đáy của khối trụ ngoại tiếp khối chóp đều S.ABC trong các trường hợp sau:

a. ABC là tam giác vuông tại A có $AB=a$ và $AC=a\sqrt{3}$

b. ABC có $AB=5;AC=7;BC=8$

Lời giải:

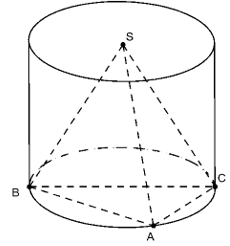
a. Cạnh huyền :

$$\begin{gathered} BC=\sqrt{A{B}^2+AC{\text{}}^2} \\ =\sqrt{a^2+3a^2}=2a \end{gathered}$$

Do ABC vuông tại A nên bán kính $R=\frac{1}{2}BC=a$

b. Nửa chu vi tam giác ABC là $p=\frac{5+7+8}{2}=10$

$$\begin{gathered} \Rightarrow S=\sqrt{10.\left(10-5\right)\left(10-7\right)\left(10-8\right)} \\ =10\sqrt{3} \\ \Rightarrow R=\frac{abc}{4S}=\frac{\mathrm{5.7.8}}{40\sqrt{3}}=\frac{7\sqrt{3}}{3} \end{gathered}$$

VD2. Cho khối trụ ngoại tiếp hình lập phương cạnh 2a. Bán kính khối trụ đã cho bằng?

Lời giải:

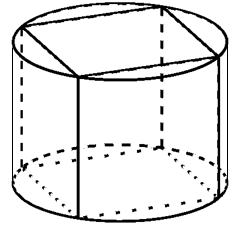
Bán kính khối trụ đã cho là: 

$R=\frac{2a\sqrt{2}}{2}=a\sqrt{2}$

c. Đáy là đường tròn nội tiếp đa giác

- Nội tiếp tam giác bất kì: $R=\frac{S}{p}$ với S là diện tích tam giác và p là nửa chu vi

- Nội tiếp tam giác đều: $R=\mathrm{canh}\cdot \frac{\sqrt{3}}{6}$

- Nội tiếp hình vuông: $\mathrm{R}=\frac{\text{ canh }}{2}$

VD1. Cho hình trụ nội tiếp trong một hình lập phương có cạnh a. Tính bán kính của hình trụ đó. 

Lời giải:

Bán kính hình trụ là $R=\frac{a}{2}$

VD2. Cho lăng trụ đều ABC.A’B’C’ có $AA\text{'}=a$, thể tích $\frac{a^3\sqrt{3}}{2}$ ngoại tiếp khối trụ. Tính bán kính khối trụ đó.

Lời giải:

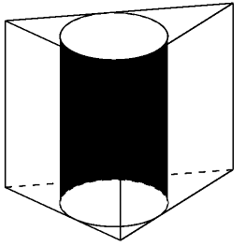
Thể tích khối lăng trụ là :

$$\begin{gathered} V=h.S_d\iff \frac{a^3\sqrt{3}}{2}=a.S_d \\ \Rightarrow S_d=\frac{a^2\sqrt{3}}{2} \end{gathered}$$

Đáy lăng trụ đều là tam giác đều nên :

$$\begin{gathered} {\mathrm{S}}_{\mathrm{d}}={\mathrm{canh}}^2\frac{\sqrt{3}}{4} \\ \Rightarrow \mathrm{canh}=\mathrm{a}\sqrt{2} \end{gathered}$$

Do vậy bán kính đáy hình trụ là: $R=\frac{a\sqrt{2}.\sqrt{3}}{6}=\frac{a}{\sqrt{6}}$

d. Thiết diện qua trục là hình vuông; hình chữ nhật

VD. Tính bán kính hình trụ chiều cao $h=3$ trong các trường hợp sau:

a. Thiết diện qua trục là hình vuông

b. Thiết diện qua trục là hình chữ nhật có diện tích là 15.

Lời giải:

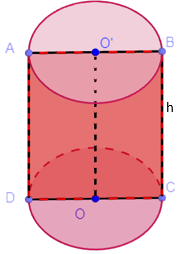
Ta hình dung thiết diện qua trục chính là tứ giác ABCD

a. Do ABCD là hình vuông nên $CD=h=3$

$\Rightarrow$Bán kính hình trụ là $R=\frac{1}{2}CD=\frac{3}{2}$

b. Chiều dài của hình chữ nhật là $CD=15:3=5$

Suy ra bán kính hình trụ là $R=\frac{CD}{2}=\frac{5}{2}$