Giá trị lớn nhất, giá trị nhỏ nhất của hàm số và cách giải - Toán lớp 12

A. LÝ THUYẾT

1. Định nghĩa

Giả sử hàm số f(x) xác định trên tập K ( $K\subset R$) Khi đó:

a)  Nếu tồn tại một điểm $x_0\in K$ sao cho $f\left(x\right)\le f\left(x_0\right),\forall x\in K$ thì số $M=f\left(x_0\right)$  được gọi là giá trị lớn nhất của hàm số f(x) trên K. Kí hiệu: $M=\underset{x\in D}{\max }f\left(x\right)$ .

b)  Nếu tồn tại một điểm $x_0\in K$ sao cho $f\left(x\right)\ge f\left(x_0\right),\forall x\in K$ thì số $m=f\left(x_0\right)$ được gọi là giá trị nhỏ nhất của hàm số f(x) trên K. Kí hiệu: $M=\underset{x\in D}{\min }f\left(x\right)$.

2. Nhận xét.

- Như vậy để có được M (hoặc m) là giá trị lớn nhất (giá trị nhỏ nhất) của hàm số f(x) trên K ta phải chỉ ra được:

a) $f\left(x\right)\le M$ (hoặc $f\left(x\right)\ge m$) với mọi $x\in K$.

b) Tồn tại ít nhất một điểm $x_0\in K$ sao cho $f\left(x_0\right)=M$ (hoặc $f\left(x_0\right)=m$ ).

- Chú ý khi nói đến giá trị lớn nhất hay giá trị nhỏ nhất của hàm số f(x) (mà không nói rõ “trên tập K’’) thì ta hiểu đó là giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.

- Mỗi hàm số liên tục trên đoạn [a;b] thì đạt được giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

Hơn nữa:

a) Nếu hàm số f(x) đồng biến trên đoạn [a;b] thì $\underset{x\in D}{\max }f\left(x\right)=f\left(b\right)$ và $\underset{x\in D}{\min }f\left(x\right)=f\left(a\right)$

b) Nếu hàm số f(x) nghịch biến trên đoạn [a;b] thì $\underset{x\in D}{\min }f\left(x\right)=f\left(b\right)$ và $\underset{x\in D}{max}f\left(x\right)=f\left(a\right)$

- Cho phương trình $f\left(x\right)=m$ với $y=f\left(x\right)$ là hàm số liên tục trên D thì phương trình có nghiệm khi $\underset{D}{\min }f\left(x\right)\le m\le \underset{D}{\max }f\left(x\right)$.

- Một hàm số có thể đồng thời đạt được giá trị lớn nhất và giá trị nhỏ nhất trên một tập K hoặc chỉ đạt được giá trị nhỏ nhất hoặc chỉ đạt được giá trị lớn nhất hoặc không tồn tại cả hai giá trị này. Chẳng hạn:

a) Xét hàm số bậc hai $y=a{x}^2+bx+c$ trên tập xác định K = R.

+ Khi a > 0 thì hàm số có đạt được giá trị nhỏ nhất tại $x=\frac{-b}{2a}$ đồng thời bằng giá trị cực tiểu của hàm số tại $x=\frac{-b}{2a}$.

 + Khi a < 0 thì hàm số có đạt được giá trị lớn nhất tại $x=\frac{-b}{2a}$ đồng thời bằng giá trị cực đại của hàm số tại $x=\frac{-b}{2a}$ .

b) Xét trên tập K = R hàm số bậc ba $y=a{x}^3+b{x}^2+cx+d$ không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.

c) Xét trên $K=ℝ\backslash \left\{\frac{-c}{d}\right\}$ hàm số $y=\frac{ax+b}{cx+d}$ không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.

d) Xét hàm số trùng phương $y=a{x}^4+b{x}^2+c$ trên tập xác định K = R.

+ Khi a > 0 thì hàm số đạt được giá trị nhỏ nhất đồng thời bằng giá trị cực tiểu của hàm số.

+ Khi a < 0 thì hàm số đạt được giá trị lớn nhất đồng thời bằng giá trị cực đại của hàm số.

B. CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.

Dạng 1. Tìm GTLN, GTNN của hàm số trên 1 đoạn.

1. Phương pháp giải.

Phương pháp: Cho hàm số $y=f\left(x\right)$ xác định và liên tục trên $\left[a;b\right]$.

Bước 1. Tính đạo hàm $f^{\text{'}}\left(x\right)$.

Bước 2. Tìm tất cả các nghiệm $x_i\in [a;b]$ của phương trình $f^{\text{'}}\left(x\right)=0$ và tất cả các điểm ${\alpha }_i\in [a;b]$ làm cho $f^{\text{'}}\left(x\right)$ không xác định.

Bước 3. Tính $f\left(a\right)$, $f\left(b\right)$, $f\left(x_i\right)$, $f\left({\alpha }_i\right)$.

Bước 4. So sánh các giá trị tính được và kết luận $M=\underset{\left[a;b\right]}{\max }f\left(x\right)$, $m=\underset{\left[a;b\right]}{\min }f\left(x\right)$.

Lưu ý:

- Đối với bài toán tìm GTLN, GTNN trên khoảng, nửa đoạn làm tương tự.

- Trong trường hợp trên khoảng đó không tồn tại giá trị f’(x) = 0 hoặc không xác định thì kết luận không tìm được GTLN, GTNN trên khoảng đó.

- Đối với bài toán xét trên cả tập xác định, tham khảo phần A.5 Lý thuyết.

2. Ví dụ minh hoạ.

Ví dụ 1. Giá trị nhỏ nhất của hàm số $f\left(x\right)=x^4-10x^2-2$ trên đoạn $\left[0;9\right]$ bằng:

A. -2

B. -11

C. -26

D. -27

Lời giải

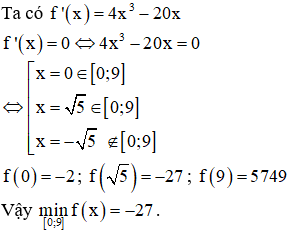
Chọn D.

Ví dụ 2. Trên đoạn $[-2;1]$, hàm số $y=x^3-3x^2-1$ đạt giá trị lớn nhất tại điểm:

A. $x=-2$

B. $x=0$

C. $x=-1$

D. $x=1$ .

Lời giải

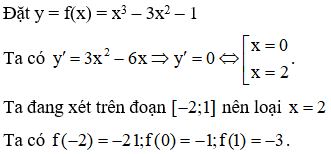
Do đó giá trị lớn nhất của hàm số trên đoạn $[-2;1]$ là -1, tại  x =0.

Chọn B.

Ví dụ 3. Tìm giá trị lớn nhất  của hàm số $f\left(x\right)=\sqrt{x-1}+\sqrt{3-x}-2\sqrt{-x^2+4x-3}$

A. $M=0.$

B. $M=-\sqrt{2}.$

C. $M=\sqrt{2}.$

D. $M=\frac{9}{4}.$

Lời giải

TXĐ: Đặt  $\text{D}=\left[1;3\right].$

Chọn C.

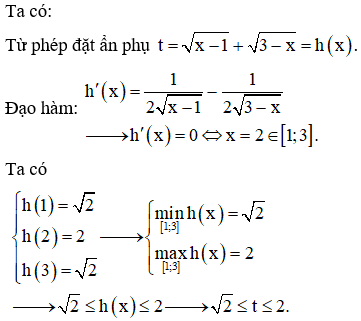
Ví dụ 4. Tìm giá trị lớn nhất M của hàm số $f\left(x\right)=\left|-x^2-4x+5\right|$ trên đoạn $\left[-6;6\right]$.

A. $M=0.$

B. $M=9$

C. $M=55$

D. $M=110.$

Lời giải

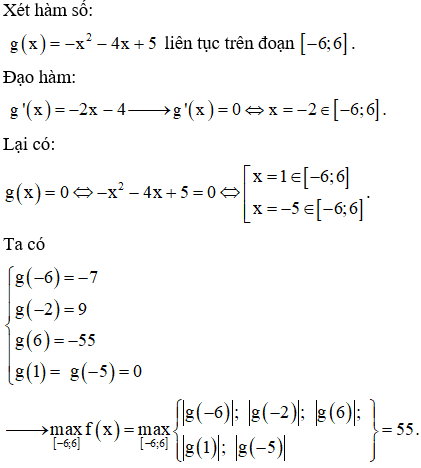
Chọn C.

Lưu ý: Hàm trị tuyệt đối không âm.

Ví dụ 5. Tìm giá trị nhỏ nhất m của hàm số $f\left(x\right)=2{\cos }^{3}x-\frac{9}{2}{\cos }^{2}x+3\cos x+\frac{1}{2}$

A. $m=-24.$

B. $m=-12$

C. $m=-9.$

D. $m=-1$

Lời giải

Đặt $t=\cos x\left(-1\le t\le 1\right).$

Khi đó, bài toán trở thành Tìm giá trị nhỏ nhất của hàm số $g\left(t\right)=2t^3-\frac{9}{2}{t}^2+3t+\frac{1}{2}$ trên đoạn $\left[-1;1\right]\text{'}\text{'}$.

Đạo hàm:

$$\begin{gathered} g\text{'}\left(t\right)=6t^2-9t+3\stackrel{}{\to }g\text{'}\left(t\right)=0 \\ \iff \left[\begin{array}{l}t=1\in \left[-1;1\right]\\ t=\frac{1}{2}\in \left[-1;1\right]\end{array}\right.. \end{gathered}$$

Ta có :

$$\begin{gathered} \left\{\begin{array}{l}g\left(-1\right)=-9\\ g\left(\frac{1}{2}\right)=\frac{9}{8}\\ g\left(1\right)=1\end{array}\right.\stackrel{}{\to }\underset{\left[-1;1\right]}{\min }g\left(t\right) \\ =g\left(-1\right)=-9\stackrel{}{\to }\underset{x\in ℝ}{\min }f\left(x\right)=-9. \end{gathered}$$

Chọn C.

Ví dụ 6. Giá trị lớn nhất của hàm số $f\left(x\right)=\frac{x-m^2}{x+1}$ trên đoạn $\left[0;1\right]$ bằng:

A. $\frac{1+m^2}{2}$

B. $-m^2$

C. $\frac{1-m^2}{2}$

D. $m^2$

Lời giải

Đạo hàm :

$f\text{'}\left(x\right)=\frac{1+m^2}{{\left(x+1\right)}^2}>0,\forall x\in \left[0;1\right]$

Suy ra hàm số $f\left(x\right)$ đồng biến trên [ 0;1]

$\left[0;1\right]\stackrel{}{\to }\underset{\left[0;1\right]}{\max }f\left(x\right)=f\left(1\right)=\frac{1-m^2}{2}.$

Chọn C.

3. Bài tập tự luyện.

Câu 1. Giá trị nhỏ nhất của hàm số $f\left(x\right)=x^3-21x$ trên đoạn [2;19] bằng:

A. 36.

B. $-14\sqrt{7}$

C. $14\sqrt{7}$

D. -34.

Câu 2. Giá trị nhỏ nhất của hàm số $f\left(x\right)=x^3-24x$ trên đoạn $\left[2;19\right]$bằng:

A. $32\sqrt{2}$

B. -40

C. $-32\sqrt{2}$

D. -45

Câu 3. Tìm giá trị lớn nhất  M của hàm số $y=x^4-2x^2+3$ trên đoạn $\text{[}0;\sqrt{3}\text{]}$:

A. 3.

B. -6.

C. 10.

D. 6.

Câu 4. Tìm giá trị nhỏ nhất m của hàm số $y=x^4-x^2+13$ trên đoạn [0;4]:

A. $m=\frac{51}{4}$

B. $m=\frac{49}{4}$

C. m = 13

D.  $m=\frac{51}{2}$

Câu 5. Tìm giá trị nhỏ nhất m của $y=x^2+\frac{2}{x}$  trên đoạn  $\left[\frac{1}{2};2\right]$ .

A. $m=\frac{17}{4}$

B. $m=10$

C. $m=5$

D. $m=3$

Câu 6. Gọi $M,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right)=2x^3+3x^2-1$ trên đoạn $\left[-2;-\frac{1}{2}\right]$. Tính $P=M-m$.

A. $P=-5$

B. $P=1$

C. $P=4$

D. $P=5$

Câu 7. Xét hàm số $y=\sqrt{4-3x}$ trên đoạn $\left[-1;1\right]$. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên đoạn $\left[-1;1\right]$.

B. Hàm số có cực trị trên khoảng $\left(-1;1\right)$.

C. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn $\left[-1;1\right]$.

D. Hàm số có giá trị nhỏ nhất bằng 1 khi x = 1, giá trị lớn nhất bằng $\sqrt{7}$ khi x = - 1.

Câu 8. Khi tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\sqrt{-x^2+3x+4}$, một học sinh làm như sau:

 (1). Tập xác định $D=\left[-1;4\right]$ và $y\text{'}=\frac{-2x+3}{\sqrt{-x^2+3x+4}}$.

(2). Hàm số không có đạo hàm tại $x=-1;x=4$ và $\forall x\in \left(-1;4\right):y\text{'}=0\iff x=\frac{3}{2}$.

(3). Kết luận: Giá trị lớn nhất của hàm số bằng $\frac{5}{2}$ khi  $x=\frac{3}{2}$ và giá trị nhỏ nhất bằng 0 khi $x=-1;x=4$.

Cách giải trên:

A. Sai ở bước (3).

B. Sai từ bước (1).

C. Sai từ bước (2).

D. Cả ba bước  (1), (2), (3) đều đúng.

Câu 9. Khi tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=x+\sqrt{2-x^2}$, một học sinh làm như sau:

 (1). Tập xác định: $D=\left[-\sqrt{2};\sqrt{2}\right]$ và $y\text{'}=\frac{\sqrt{2-x^2}-x}{\sqrt{2-x^2}}$.

 (2).

$y\text{'}=0\iff \sqrt{2-x^2}-x=0$

$\iff \left\{\begin{array}{l}x\ge 0\\ 2-x^2=x^2\end{array}\right.\iff x=1$

 (3). Kết luận: Giá trị lớn nhất của hàm số bằng 2 khi x = 1 và giá trị nhỏ nhất bằng $-\sqrt{2}$ khi $x=-\sqrt{2}$.

Cách giải trên:

A. Sai từ bước (1).

B. Sai từ bước (2).

C. Sai ở bước (3).

D. Cả ba bước (1), (2), (3) đều đúng.

Câu 10. Tìm giá trị nhỏ nhất của hàm số $y=\frac{x^2+3}{x-1}$ trên đoạn [2;4].

A. $\underset{\left[2;4\right]}{\min y}=6$

B. $\underset{\left[2;4\right]}{\min y}=-2$

C. $\underset{\left[2;4\right]}{\min y}=-3$

D. $\underset{\left[2;4\right]}{\min y}=\frac{19}{3}$

Câu 11. Giá trị lớn nhất của hàm số $f\left(x\right)=\left|x^2-3x+2\right|-x$ trên đoạn $\left[-4;4\right]$ bằng:

A. 2.

B. 17.

C. 34.

D. 68.

Câu 12. Trên nửa khoảng $\left[0;+\infty \right)$, hàm số $f\left(x\right)=x^3+x-\cos x-4$:

A. Có giá trị lớn nhất là - 5, không có giá trị nhỏ nhất.

B. Không có giá trị lớn nhất, có giá trị nhỏ nhất là - 5.

C. Có giá trị lớn nhất là , giá trị nhỏ nhất là .

D. Không có giá trị lớn nhất, không có giá trị nhỏ nhất.

Câu 13. Hàm số nào sau đây không có giá trị nhỏ nhất và giá trị lớn nhất trên $\left[-2;2\right]$

A. $y=x^3+2$

B. $y=x^4+x^2$

C. $y=\frac{x-1}{x+1}$

D. $y=-x+1$

Câu 14. Biết rằng hàm số $f\left(x\right)=x^3-3x^2-9x+28$ đạt giá trị nhỏ nhất trên đoạn $\left[0;4\right]$ tại $x_0$. Tính  $P=x_0+2018.$

A. $P=3.$

B. $P=2019.$

C. $P=2021.$

D. $P=2018.$

Câu 15. Tìm giá trị nhỏ nhất của hàm số $f\left(x\right)=\frac{x^2+3}{x-1}$ trên đoạn $\left[2;4\right]$.

A. $\underset{\left[2;4\right]}{\min }f\left(x\right)=6$

B. $\underset{\left[2;4\right]}{\min }f\left(x\right)=-2$

C. $\underset{\left[2;4\right]}{\min }f\left(x\right)=-3$

D. $\underset{\left[2;4\right]}{\min }f\left(x\right)=\frac{19}{3}$

Câu 16. Tập giá trị của hàm số $f\left(x\right)=x+\frac{9}{x}$ với $x\in \left[2;4\right]$ là đoạn $\left[a;b\right]$. Tính $P=b-a$.

A. $P=6$

B. $P=\frac{13}{2}$

C. $P=\frac{25}{4}$

D. $P=\frac{1}{2}$

Câu 17. Cho hàm số $f\left(x\right)=\frac{2x^2+x+1}{x+1}$. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn $\left[0;1\right].$

A. $M=\sqrt{2};m=1.$

B. $M=2;m=1.$

C.  $M=1;m=-2.$

D. $M=2;m=\sqrt{2}.$

Câu 18. Cho hàm số $y=f\left(x\right)$ và có bảng biến thiên trên $\left[-5;7\right)$ như sau: 

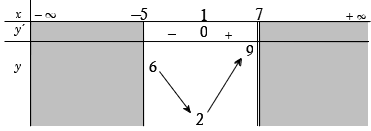
Mệnh đề nào sau đây là đúng?

A. $\underset{\left[-5;7\right)}{\min }f\left(x\right)=2$  và hàm số không đạt giá trị lớn nhất trên $\left[-5;7\right)$.

 B. $\underset{\left[-5;7\right)}{\max }f\left(x\right)=6$  và $\underset{\left[-5;7\right)}{\min }f\left(x\right)=2$.

C.  $\underset{\left[-5;7\right)}{\max }f\left(x\right)=9$ và $\underset{\left[-5;7\right)}{\min }f\left(x\right)=2$.

D. $\underset{\left[-5;7\right)}{\max }f\left(x\right)=9$  và $\underset{\left[-5;7\right)}{\min }f\left(x\right)=6$.

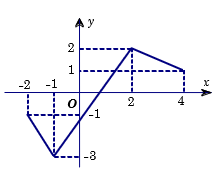
Câu 19. Cho hàm số $y=f\left(x\right)$ có đồ thị trên đoạn $\left[-2;4\right]$ như hình vẽ. Tìm giá trị lớn nhất M của hàm số $y=\left|f\left(x\right)\right|$ trên đoạn  $\left[-2;4\right]$

A. $M=2.$

B. $M=\left|f\left(0\right)\right|.$

C. $M=3$

D. $M=1$

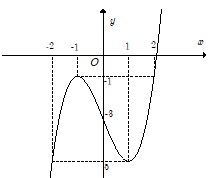
Câu 20. Cho hàm số $y=f\left(x\right)$ xác định và liên tục trên R, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số $y=f\left(x\right)$ trên đoạn $\left[-2;2\right]$.

A.  $m=-5,M=0.$

B. $m=-5,M=-1.$

C. $m=-1,M=0.$

D. $m=-2,M=2.$

Câu 21. Tìm giá trị lớn nhất M của hàm số $f\left(x\right)=\frac{\sin x+1}{{\sin }^{2}x+\sin x+1}$.

A. $M=1.$

B. $M=\frac{90}{91}.$

C. $M=\frac{110}{111}.$

D. $M=\frac{70}{79}.$

Câu 22. Tìm giá trị lớn nhất M của hàm số $f\left(x\right)={\sin }^{3}x+\cos 2x+\sin x+3$.

A. $M=0.$

B. $M=5$

C. $M=4$

D. $M=\frac{112}{27}.$

Câu 23. Cho hàm số $y=f\left(x\right)$ xác định, liên tục trên R và có bảng biến thiên như sau:

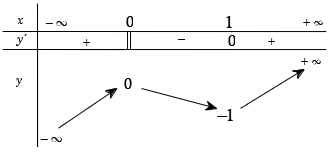
Khẳng định nào sau đây là đúng ?

A. Hàm số có đúng một cực trị.

B. Hàm số có giá trị cực tiểu bằng 1.

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.

D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1.

Câu 24. Tìm giá trị thực của tham số a để hàm số $f\left(x\right)=-x^3-3x^2+a$ có giá trị nhỏ nhất trên đoạn $\left[-1;1\right]$ bằng 0.

A. $a=2.$

B. $a=6$

C. $a=0$

D. $a=4$

Câu 25. Giá trị lớn nhất của hàm số $y=\frac{x-m^2}{x+1}$trên $\left[0;1\right]$ bằng:

A. $\frac{1+m^2}{2}$

B. $-m^2$

C. $\frac{1-m^2}{2}$

D. Đáp án khác.

Câu 26. Cho hàm số $f\left(x\right)=x^3+\left(m^2+1\right)x+m^2-2$ với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn $\left[0;2\right]$ bằng 7 

A. $m=\pm 1$

B. $m=\pm \sqrt{7}$

C. $m=\pm \sqrt{2}$

D. $m=\pm 3$

Câu 27. Cho hàm số $y=\frac{x+m}{x-1}$ (với  là tham số thực) thỏa mãn $\underset{\left[2;4\right]}{\min }y=3$. Mệnh đề nào dưới đây là đúng?

A. $3<m\le 4.$

B. $1\le m<3.$

C. $m>4.$

D. $m<-1.$

Câu 28. Cho hàm số $y=\frac{x+m}{x+1}$ (m là tham số thực) thoả mãn $\underset{\left[1;2\right]}{\min }y+\underset{\left[1;2\right]}{\max }y=\frac{16}{3}$. Mệnh đề nào dưới đây đúng ?

A. m = 1.

B. m = 5.

C. m = 3.

D. m = 2.

Câu 29. Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số$f\left(x\right)=\frac{x-m^2+m}{x+1}$  trên đoạn [0;1] bằng - 2?

A. $\left[\begin{array}{l}m=1\\ m=2\end{array}\right.$

B. $\left[\begin{array}{l}m=1\\ m=-2\end{array}\right.$

C. $\left[\begin{array}{l}m=-1\\ m=-2\end{array}\right.$

D. $\left[\begin{array}{l}m=-1\\ m=2\end{array}\right.$

Câu 30. Cho hàm số $f\left(x\right)=\frac{2\sqrt{x}+m}{\sqrt{x+1}}$ với m là tham số thực. Tìm tất cả các giá trị của m >1 để hàm số có giá trị lớn nhất trên đoạn $\left[0;4\right]$ nhỏ hơn  3.

A. $m\in \left(1;3\right).$

B. $m\in \left(1;3\sqrt{5}-4\right).$

C. $m\in \left(1;\sqrt{5}\right).$

D. $m\in \left(1;3\right].$

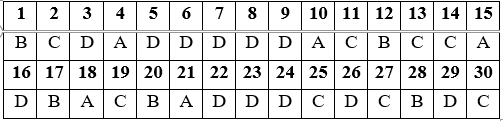
Đáp án

Dạng 2. Ứng dụng GTLN, GTNN của hàm số vào bài toán thực tế.

1. Phương pháp giải:

Bước 1: Từ các điều kiện của bài toán xây dựng hàm số.

Bước 2: Tìm tập xác định của hàm số.

Bước 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số vừa xây dựng trên tập xác định của nó phù hợp với yêu cầu bài toán.

Bước 4:  Kết luận.

2. Ví dụ minh hoạ.

Ví dụ 1. Trong tất cả các hình chữ nhật có cùng diện tích  thì hình chữ nhật có chu vi nhỏ nhất bằng bao nhiêu?

A. $2\sqrt{S}$

B. $4\sqrt{S}$

C. $2S$

D. $4S$

Lời giải

Gọi $a,b>0$ lần lượt là chiều dài và chiều rộng của hình chữ nhật cần tìm.

Diện tích của hình chữ nhật: $S=ab$.

Chu vi hình chữ nhật:  

$C=2\left(a+b\right)=2a+\frac{2S}{a}.$

Khảo sát hàm $f\left(a\right)=2a+\frac{2S}{a}$ trên $\left(0;+\infty \right)$, ta được $\min f\left(a\right)=4\sqrt{S}$ khi $a=\sqrt{S}$. 

Chọn B.

Cách 2. Ta có :

$$\begin{gathered} P=2\left(a+b\right)\ge 2.2\sqrt{ab} \\ =4\sqrt{ab}=4\sqrt{S} \end{gathered}$$

Dấu " = " xảy ra $\iff a=b$.

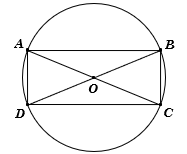
Ví dụ 2. Một mảnh vườn hình chữ nhật có diện tích $961{\text{m}}^{\text{2}}$, người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm của hình chữ nhật (xem hình minh họa). Tính diện tích nhỏ nhất $S_{\min }$ của 4 phần đất được mở rộng.

A. $S_{\min }=961\pi -961\left({\text{m}}^{\text{2}}\right).$

B. $S_{\min }=1922\pi -961\left({\text{m}}^{\text{2}}\right).$

C. $S_{\min }=1892\pi -946\left({\text{m}}^{\text{2}}\right).$

D. $S_{\min }=480,5\pi -961\left({\text{m}}^{\text{2}}\right).$

Lời giải

Gọi  $x\left(\text{m}\right),y\left(\text{m}\right)$ $\left(x>0,y>0\right)$ lần lượt là hai kích thước mảnh vườn hình chữ nhật; $R\left(\text{m}\right)$ là bán kính hình tròn ngoại tiếp mảnh vườn $\stackrel{}{\to }{R}^2=O{B}^2=\frac{x^2+y^2}{4}.$

Theo đề bài, ta có $xy=961{\text{m}}^{\text{2}}$.

Diện tích 4 phần đất mở rộng:

$S=S_{\text{tron}}-S_{ABCD}=\pi R^2-xy$

$$\begin{gathered} =\pi .\frac{\left(x^2+y^2\right)}{4}-xy\stackrel{\text{Cosi}}{\ge }\pi .\frac{2xy}{4}-xy \\ =480,5\pi -961. \end{gathered}$$

Chọn D.

Nhận xét. Dấu "=" xảy ra khi ABCD là hình vuông. Nếu phát hiện đều này thì làm trắc nghiệm rất nhanh.

3. Bài tập vận dụng.

Câu 1. Trong tất cả các hình chữ nhật có cùng chu vi bằng 16cm thì hình chữ nhật có diện tích lớn nhất bằng:

A. $36{\text{cm}}^{\text{2}}$

B. $20{\text{cm}}^{\text{2}}$

C. $16{\text{cm}}^{\text{2}}$

D. $30{\text{cm}}^{\text{2}}$

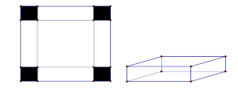
Câu 2. Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left(\text{cm}\right)$, rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

A. $x=6$

B. $x=3$

C. $x=2$

D. $x=4$

Câu 3. Tính diện tích lớn nhất $S_{\max }$ của hình chữ nhật nội tiếp trong nửa đường tròn có bán kính 10cm, biết một cạnh của hình chữ nhật nằm dọc theo đường kính của đường tròn.

A. $S_{\max }=80{\text{cm}}^{\text{2}}.$

B. $S_{\max }=100{\text{cm}}^{\text{2}}.$

C. $S_{\max }=160{\text{cm}}^{\text{2}}.$

D. $S_{\max }=200{\text{cm}}^{\text{2}}.$

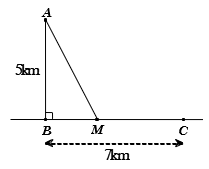
Câu 4. Một ngọn hải đăng đặt ở vị trí  cách bờ biển một khoảng $AB=5\text{km}$. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7km. Người canh hải đăng có thể chèo đò từ A đến vị trí M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Vị trí của điểm M cách B một khoảng gần nhất với giá trị nào sau đây để người đó đến kho nhanh nhất?

A. $3,0\text{km}.$

B. $7,0\text{km}.$

C. $4,5\text{km.}$

D.  $2,1\text{km}.$   

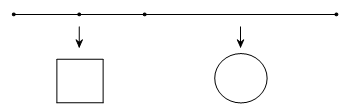
Câu 5. Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh a, đoạn dây thứ hai uốn thành đường tròn bán kính r. Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì tỉ số $\frac{a}{r}$ bằng:

A. $\frac{a}{r}=1.$

B. $\frac{a}{r}=2.$

C. $\frac{a}{r}=3.$

D. $\frac{a}{r}=4.$

Câu 6. Một mảnh giấy hình chữ nhật có chiều dài 12cm và chiều rộng 6cm. Thực hiện thao tác gấp góc dưới bên phải sao cho đỉnh được gấp nằm trên cạnh chiều dài còn lại. Hỏi chiều dài L tối thiểu của nếp gấp là bao nhiêu?

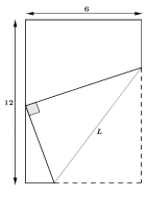
A. $\min L=6\sqrt{2}\text{ cm}$

B. $\min L=\frac{9\sqrt{3}}{2}\text{ cm}$

C. $\min L=\frac{7\sqrt{3}}{2}\text{ cm}$

D. $\min L=9\sqrt{2}\text{ cm}$                             

Đáp án