Công thức lũy thừa đầy đủ, chi tiết nhất - Toán lớp 12

1. Lí thuyết

a. Lũy thừa với số mũ nguyên

- Lũy thừa với số mũ nguyên dương

Cho $a\in ℝ$, $n\in {\mathbb{N}}^{*}$. Khi đó: $a^n=\underset{nsôa}{\underbrace{a.a\mathrm{...}a}}$

- Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0

Cho $a\ne 0$. Khi đó: $a^{-n}=\frac{1}{a^n};a^0=1$

VD: $2^{-3}=\frac{1}{2^3}=\frac{1}{8}$

- Chú ý: Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa với số mũ nguyên dương.

+ $0^0$ và $0^{-n}$ không có nghĩa.

b. Căn bậc n

- Cho số thực b và số nguyên dương $n\ge 2$.

Số a được gọi là căn bậc n của số b nếu $a^n=b$

VD: 4 là căn bậc ba của 64 vì $4^3=64$

- Khi n lẻ, $b\in ℝ$: Tồn tại duy nhất $\sqrt[n]{b}$

c. Lũy thừa với số mũ hữu tỉ

- Cho số thực $a>0$ và số hữu tỉ $r=\frac{m}{n}$, trong đó $m\in \mathbb{Z},n\ge 2$

Khi đó: $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$. VD: $2^{\frac{1}{3}}=\sqrt[3]{2}$

d. Lũy thừa với số mũ vô tỉ

- Giả sử a là một số dương, $\alpha$ là một số vô tỉ, $\left(r_n\right)$ là một dãy số hữu tỉ sao cho $\underset{n\to +\infty }{\lim }{r}_n=\alpha$. Khi đó: $a^{\alpha }=\underset{n\to +\infty }{\lim }{a}^{r_n}$

2. Các tính chất của lũy thừa

Cho 2 số dương a, b; $m,n\in ℝ$. Khi đó:

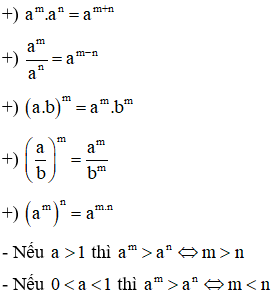
3. Ví dụ

VD1. Cho a, b là các số dương. Hãy viết rút gọn các biểu thức sau dưới dạng lũy thừa:

a. $a^{\frac{1}{3}}.\sqrt{a}$

b. $b^{\frac{1}{2}}.b^{\frac{1}{3}}.\sqrt[6]{b}$

c. $\sqrt[3]{b}:b^{\frac{1}{6}}$

Lời giải:

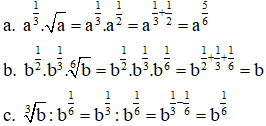
VD2. Tìm x biết:

a. $x^8-15x^4-16=0$

b. $x^6+6x^3-16=0$

Lời giải:

VD3. Cho a và b là các số dương. Rút gọn các biểu thức

a. $A=\frac{a^{\frac{4}{3}}\left(a^{-\frac{1}{3}}+a^{\frac{2}{3}}\right)}{a^{\frac{1}{4}}\left(a^{\frac{3}{4}}+a^{-\frac{1}{4}}\right)}$

b. $B=\left(\sqrt[3]{a}+\sqrt[3]{b}\right).\left(a^{\frac{2}{3}}+b^{\frac{2}{3}}-\sqrt[3]{ab}\right)$

Lời giải:

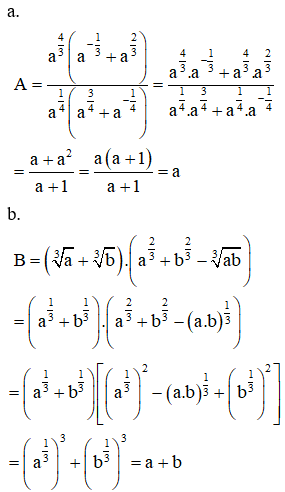
4. Luyện tập

Bài 1. Tính

a. $2^{2-3\sqrt{5}}{.8}^{\sqrt{5}}$

b. $3^{1+2\sqrt[3]{2}}:9^{\sqrt[3]{2}}$

c. $\left(4^{2\sqrt{3}}-4^{\sqrt{3}-1}\right){.2}^{-2\sqrt{3}}$

Bài 2. Rút gọn và tính giá trị của biểu thức

a. $A=\sqrt[3]{a}.\sqrt[6]{a}$ với $a=0,09$

b. $\frac{\sqrt{b}.\sqrt[3]{b^2}}{\sqrt[6]{b}}$ với $b=1,3$

c. $C=\frac{\sqrt[3]{a}.\sqrt[4]{a}.\sqrt[12]{a^5}}{a^{-\frac{1}{3}}}$ với $a=2,7$

Bài 3. Cho x và y là 2 số dương. Rút gọn các biểu thức sau:

a. $\frac{x^{\frac{1}{3}}\sqrt{y}+y^{\frac{1}{3}}\sqrt{x}}{\sqrt[6]{x}+\sqrt[6]{y}}$

b. $\left(x^{\frac{1}{3}}+y^{\frac{1}{3}}\right):\left(2+\sqrt[3]{\frac{x}{y}}+\sqrt[3]{\frac{y}{x}}\right)$

Bài 4. So sánh các số sau với 1

a. $3^{-2}$

b. ${\left(\frac{1}{2}\right)}^{\sqrt{5}}$

c. ${\left(\frac{\pi }{3}\right)}^{\sqrt{5}-2}$

Bài 5. So sánh các cặp số sau:

a. $\sqrt{17}$ và  $\sqrt[3]{28}$

b. $\sqrt[4]{13}$ và $\sqrt[5]{23}$

c. ${\left(\frac{2}{3}\right)}^{\sqrt{3}}$ và ${\left(\frac{2}{3}\right)}^{\sqrt{2}}$

d. $3^{\sqrt{5}}$ và $3^{\sqrt{3}+1}$

Bài 6. Giải phương trình

a. $x^{10}-x^5-2=0$

b. $x^9-7x^3+6=0$