33 câu hỏi trắc nghiệm thuộc Đề số 1

Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề số 1

6650 lượt thi
33 câu hỏi
90 phút

Danh sách câu hỏi

Câu 1:

Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là

\frac{4}{3} B h

B. $3 B h$

C. $\frac{1}{3} B h$

D. $B h$

Xem đáp án

Đáp án D

Theo công thức tính thể tích lăng trụ.

Câu 2:

Cho cấp số cộng với $u_{1} = 3$ và $u_{2} = 9.$ Công sai của cấp số cộng đã cho bằng

A. $- 6.$

B. 3.

C. 12.

D. 6.

Xem đáp án

Đáp án D

Ta có: $d = u_{2} - u_{1} = 6.$

Câu 3:

Cho hàm số $f (x)$ có bảng biến thiên:

Hàm số đã cho đồng biến trên khoảng:

(- \infty; - 1)

(3; + \infty)

(- 2; 2)

D. $(- 1; 3)$

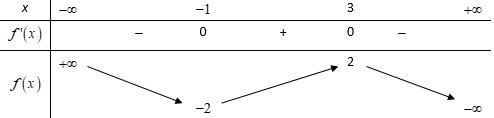
Xem đáp án

Chọn D

Dựa vào BBT ta thấy hàm số $y = f (x)$ đồng biến trên $(- 1; 3)$

Câu 4:

Thể tích của khối hình hộp chữ nhật có các cạnh lần lượt là a, 2a, 3a bằng

6 a^{3}

B. $3 a^{3}$ .

C. $a^{3}$ .

D. $2 a^{3}$ .

Xem đáp án

V = a .2 a .3 a = 6 a^{3}

(đvtt)

Chọn đáp án A

Câu 5:

Số cách chọn 2 học sinh từ 7 học sinh là

A. $2^{7} .$

B. $A_{7}^{2} .$

C. $C_{7}^{2} .$

D. $7^{2} .$

Xem đáp án

Đáp án C

Mỗi cách chọn 2 học sinh từ 7 học sinh là một tổ hợp chập 2 của 7 phần tử. Số cách chọn 2 học sinh của 7 học sinh là: $C_{7}^{2} .$

Câu 6:

Tính tích phân $I = \int_{- 1}^{0} (2 x + 1) d x \frac{1}{2}$ .

I = 0

B. $I = 1$

C. $I = 2$

D. $I = - \frac{1}{2}$

Xem đáp án

Đáp án A

$I = \int_{- 1}^{0} (2 x + 1) d x = {(x^{2} + x)|}_{- 1}^{0} = 0 - 0 = 0$

Câu 7:

Cho hàm số $y = f (x)$ có bảng biến thiên như hình vẽ bên. Giá trị cực tiểu của hàm số là số nào sau đây?

A. $- 4$

B. 3

C. 0

D. $- 1$

Xem đáp án

Chọn A

Dựa vào đồ thị hàm số ta thấy giá trị cực tiểu của hàm số là

- 4

Câu 8:

Cho

\int_{0}^{1} f (x) d x = 3, \int_{0}^{1} g (x) d x = - 2

. Tính giá trị của biểu thức

I = \int_{0}^{1} [2 f (x) - 3 g (x)] d x

A. 12

B. 9

C. 6

D. $- 6$

Xem đáp án

Chọn A

Ta có: $I = \int_{0}^{1} [2 f (x) - 3 g (x)] d x = 2 \int_{0}^{1} f (x) d x - 3 \int_{0}^{1} g (x) d x = 2.3 - 3. (- 2) = 12$

Câu 9:

Tính thể tích của khối nón có chiều cao bằng 4 và độ dài đường sinh bằng 5

A. $12 π$

B. $36 π$

C. $16 π$

D. $48 π$

Xem đáp án

Đáp án A

Bán kính đường tròn đáy của khối nón là $r = \sqrt{l^{2} - h^{2}} = 3$

Vậy thể tích của khối nón là $V = \frac{1}{3} π r^{2} h = 12 π$

Câu 10:

Cho hai số phức $z_{1} = 2 - 3 i$ và $z_{2} = 1 - i$ . Tính $z = z_{1} + z_{2}$ .

A. $z_{1} + z_{2} = 3 + 4 i$

B. $z_{1} + z_{2} = 3 - 4 i$

C. $z_{1} + z_{2} = 4 + 3 i$

D. $z_{1} + z_{2} = 4 - 3 i$

Xem đáp án

Đáp án B

Ta có: $z_{1} + z_{2} = 3 - 4 i$ .

Câu 11:

Nghiệm của phương trình $2^{2 x - 1} = 8$ là

A. $x = \frac{3}{2}$

B. $x = 2$

C. $x = \frac{5}{2}$

D. $x = 1$

Xem đáp án

Đáp án B

Ta có: $2^{2 x - 1} = 8 \Leftrightarrow 2 x - 1 = 3 \Leftrightarrow x = 2$

Câu 12:

Cho số phức z có điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm $M (3; - 5)$ . Xác định số phức liên hợp $\bar{z}$ của z.

A. $\bar{z} = 3 + 5 i .$

B. $\bar{z} = - 5 + 3 i .$

C. $\bar{z} = 5 + 3 i .$

D. $\bar{z} = 3 - 5 i .$

Xem đáp án

Chọn A

$M (3; - 5)$ là điểm biểu diễn của số phức $z = 3 - 5 i$ .

Số phức liên hợp $\bar{z}$ của z là: $\bar{z} = 3 + 5 i .$

Câu 13:

Số phức nghịch đảo của số phức $z = 1 + 3 i$ là

A. $\frac{1}{10} (1 - 3 i)$

B. $1 - 3 i$

C. $\frac{1}{\sqrt{10}} (1 + 3 i)$

D. $\frac{1}{10} (1 + 3 i)$

Xem đáp án

Chọn A

Câu 14:

Biết $F (x)$ là một nguyên hàm của $f (x) = \frac{1}{x + 1}$ và $F (0) = 2$ thì $F (1)$ bằng.

A. $\ln 2$

B. $2 + \ln 2$

C. 3.

D. 4.

Xem đáp án

Đáp án B

$F (x) = \int \frac{1}{x + 1} d x = \ln |x + 1| + C$ mà $F (0) = 2$ nên $F (x) = \ln |x + 1| + 2$ .

Do đó $F (1) = 2 + \ln 2$ .

Câu 15:

Cho số phức

z

thỏa mãn

z (1 + i) = 3 - 5 i

. Tính môđun của

z

A. $|z| = 4$

B. $|z| = \sqrt{17}$

C. $|z| = 16$

D. $|z| = 17$

Xem đáp án

Chọn B

Ta có:

z (1 + i) = 3 - 5 i

\Leftrightarrow z = \frac{3 - 5 i}{1 + i}

= - 1 - 4 i

\Rightarrow |z| = \sqrt{{(- 1)}^{2} + {(- 4)}^{2}}

= \sqrt{17}

Câu 16:

Cho hàm số $f (x)$ thỏa mãn $f^{'} (x) = 27 + \cos x$ và $f (0) = 2019.$ Mệnh đề nào dưới đây đúng?

A. $f (x) = 27 x + \sin x + 1991$

B. $f (x) = 27 x - \sin x + 2019$

C. $f (x) = 27 x + \sin x + 2019$

D. $f (x) = 27 x - \sin x - 2019$

Xem đáp án

Chọn C

$f^{'} (x) = 27 + \cos x \Rightarrow \int f^{'} (x) d x = \int (27 + \cos x) d x \Rightarrow f (x) = 27 x + \sin x + C$

Mà $f (0) = 2019 \Rightarrow 27.0 + \sin 0 + C = 2019 \Leftrightarrow C = 2019 \Rightarrow f (x) = 27 x + \sin x + 2019$

Câu 17:

Trong không gian với hệ tọa độ $O x y z,$ cho ba điểm $A (1; 3; 5), B (2; 0; 1), C (0; 9; 0) .$ Tìm trọng tâm $G$ của tam giác $A B C .$

A. $G (1; 5; 2)$

B. $G (1; 0; 5)$

C. $G (1; 4; 2)$

D. $G (3; 12; 6)$

Xem đáp án

Chọn C

Theo công thức tọa độ trọng tâm ta có

\{\begin{cases} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} = \frac{1 + 2 + 0}{3} = 1 \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} = \frac{3 + 0 + 9}{3} = 4 \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} = \frac{5 + 1 + 0}{3} = 2 \end{cases}

\Rightarrow G (1; 4; 2)

Câu 18:

Đồ thị hàm số $y = - \frac{x^{4}}{2} + x^{2} + \frac{3}{2}$ cắt trục hoành tại mấy điểm?

A. 0

B. 2

C. 4

D. 3

Xem đáp án

Chọn B

Xét phương trình

$- \frac{x^{4}}{2} + x^{2} + \frac{3}{2} = 0 \Leftrightarrow x^{4} - 2 x^{2} - 3 = 0 \Leftrightarrow (x^{2} + 1) (x^{2} - 3) = 0 \Leftrightarrow [\begin{array}{l} x^{2} + 1 = 0 \\ x^{2} - 3 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x^{2} = - 1 (V N) \\ x = \sqrt{3} \\ x = - \sqrt{3} \end{array}$

Vậy đồ thị hàm số $y = - \frac{x^{4}}{2} + x^{2} + \frac{3}{2}$ cắt trục hoành tại hai điểm.

Câu 19:

Xác định tọa độ điểm I là giao điểm của hai đường tiệm cận của đồ thị hàm số

y = \frac{2 x - 3}{x + 4} .

A. $I (2; 4)$

B. $I (4; 2)$

B. $I (2; - 4)$

D. $I (- 4; 2)$

Xem đáp án

Chọn D

Đồ thị hàm số $y = \frac{2 x - 3}{x + 4}$ có TCN $y = 2$ và TCĐ $x = - 4$ . Vậy tọa độ điểm I là giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 3}{x + 4}$ là: $I (- 4; 2)$ .

Câu 20:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

A. $y = x^{3} - 3 x^{2} + 3.$

B. $y = - x^{3} + 3 x^{2} + 3.$

C. $y = x^{4} - 2 x^{3} + 3.$

D. $y = - x^{4} + 2 x^{3} + 3.$

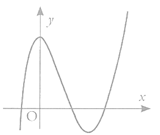
Xem đáp án

Đáp án A

Dạng hàm bậc ba nên loại C và loại D

Từ đồ thị ta có $a > 0$ do đó loại B

Câu 21:

Với a và b là hai số thực dương tùy ý và $a \neq 1, \log_{\sqrt{a}} (a^{2} b)$ bằng

A. $4 + 2 \log_{a} b$

B. $1 + 2 \log_{a} b$

C. $1 + \frac{1}{2} \log_{a} b$

D. $4 + \frac{1}{2} \log_{a} b$

Xem đáp án

Đáp án A

Ta có

\log_{\sqrt{a}} (a^{2} b) = 2 \log_{a} (a^{2} b) = 2 [\log_{a} a^{2} + \log_{a} b] = 2 (2 + \log_{a} b) = 4 + 2 \log_{a} b

Câu 22:

Một hình trụ có bán kính đáy $r = 5 c m$ , chiều cao $h = 7 c m$ . Diện tích xung quanh của hình trụ này là:

A. $35 π {cm}^{2}$

B. $70 π {cm}^{2}$

C. $\frac{70}{3} π {cm}^{2}$

D. $\frac{35}{3} π {cm}^{2}$

Xem đáp án

Đáp án B

$S_{x q} = 2 π r h = 70 π (c m^{2})$

Câu 23:

Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{x^{3}}{3} + 2 x^{2} + 3 x - 4$ trên $[- 4; 0]$ lần lượt là $M$ và $m$ . Giá trị của $M + m$ bằng

A. $\frac{4}{3}$

B. $- \frac{28}{3}$

C. $- 4$

D. $- \frac{4}{3}$

Xem đáp án

Chọn B

Hàm số $y = \frac{x^{3}}{3} + 2 x^{2} + 3 x - 4$ xác định và liên tục trên $[- 4; 0]$ .

$y^{'} = x^{2} + 4 x + 3$ $y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = - 1 (n) \\ x = - 3 (n) \end{array}$ $f (0) = - 4$ , $f (- 1) = - \frac{16}{3}$ , $f (- 3) = - 4$ , $f (- 4) = - \frac{16}{3}$

Vậy $M = - 4$ , $m = - \frac{16}{3}$ nên $M + m = - \frac{28}{3}$

Câu 24:

Số nghiệm của phương trình

\log {(x - 1)}^{2} = 2

A. 2.

B. 1.

C. 0.

D. một số khác

Xem đáp án

Chọn A

Ta có

\log {(x - 1)}^{2} = 2 = \log 10^{2} \Leftrightarrow {(x - 1)}^{2} = 100 \Leftrightarrow [\begin{array}{l} x = 11 \\ x = - 9 \end{array}

Câu 25:

Viết biểu thức $P = \sqrt[3]{x . \sqrt[4]{x}}$ ( $x > 0$ ) dưới dạng luỹ thừa với số mũ hữu tỷ.

A. $P = x^{\frac{1}{12}}$

B. $P = x^{\frac{5}{12}}$

C. $P = x^{\frac{1}{7}}$

D. $P = x^{\frac{5}{4}}$

Xem đáp án

Chọn B

Ta có:

P = {(x . x^{\frac{1}{4}})}^{\frac{1}{3}} = {(x^{\frac{5}{4}})}^{\frac{1}{3}} = x^{\frac{5}{12}}

Câu 26:

Trong không gian Oxyz, đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z}{3}$ đi qua điểm nào dưới đây

A. $(3; 1; 3)$

B. $(2; 1; 3)$

C. $(3; 1; 2)$

D. $(3; 2; 3)$

Xem đáp án

Chọn A

Thế vào.

Câu 27:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 3 = 0$ . Bán kính của mặt cầu bằng:

A. $R = 3$

B. $R = 4$

C. $R = 2$

D. $R = 5$

Xem đáp án

Chọn C

Mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 3 = 0$ có a = 1; b = 0; c = 0; d = -3 $\Rightarrow R = \sqrt{1^{2} + 0^{2} + 0^{2} - (- 3)} = 2$

Câu 28:

Tính đạo hàm của hàm số

y = 3^{x + 1}

A. $y' = 3^{x + 1} \ln 3$

B. $y' = (1 + x) {.3}^{x}$

C. $y' = \frac{3^{x + 1}}{\ln 3}$

D. $y' = \frac{3^{x + 1} . \ln 3}{1 + x}$

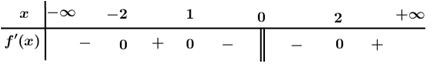
Xem đáp án

Chọn A

Ta có:

y' = (3^{x + 1})' = 3^{x + 1} \ln 3

Câu 29:

Cho hàm số

f (x)

liên tục trên

ℝ

, bảng xét dấu của

f^{'} (x)

như sau

Hàm số có bao nhiêu điểm cực tiểu

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Chọn B

Nhận thấy $y^{'}$ đổi dấu từ $-$ sang $+$ 2 lần $\Rightarrow$ Hàm số có 2 điểm cực tiểu

Câu 30:

Tập nghiệm S của bất phương trình

5^{1 - 2 x} > \frac{1}{125}

là:

A. $S = (0; 2)$

B. $S = (- \infty; 2)$

C. $S = (- \infty; - 3)$

D. $S = (2; + \infty)$

Xem đáp án

Đáp án B

$5^{1 - 2 x} > 5^{- 3} \Rightarrow 1 - 2 x > - 3 \Rightarrow x < 2$

Câu 31:

Trong không gian tọa độ Oxyz, mặt phẳng chứa trục Oz và đi qua điểm $I (1; 2; 3)$ có phương trình là

A. $2 x - y = 0$

B. $z - 3 = 0$

C. $x - 1 = 0$

D. $y - 2 = 0$

Xem đáp án

Chọn A

Mặt phẳng chứa trục Oz  mặt phẳng cần tìm có 1 VTCP là $\vec{k} = (0; 1; 1)$

$\Rightarrow \vec{k} ⊥ \vec{n}$ với $\vec{n}$ là VTPT của mặt phẳng cần tìm.

+) Xét đáp án A: có $\vec{n} = (2; - 1; 0) \Rightarrow \vec{n} . \vec{k} = 2.0 + (- 1) .0 + 0.1 = 0$

Thay tọa độ điểm $I (1; 2; 3)$ vào phương trình ta được: $2.1 - 2 = 0 \Rightarrow$ thỏa mãn

Câu 32:

Trong không gian với hệ tọa độ $O x y z$ , cho hai điểm $A (1; 2; 2)$ , $B (3; - 2; 0)$ . Một vectơ chỉ phương của đường thẳng $A B$ là:

A. $\vec{u} = (2; - 4; 2)$

B. $\vec{u} = (2; 4; - 2)$

C. $\vec{u} = (- 1; 2; 1)$

D. $\vec{u} = (1; 2; - 1)$

Xem đáp án

Chọn C

Ta có:

\vec{A B} = (2; - 4; - 2)

= - 2 (- 1; 2; 1)

Câu 33:

Trong không gian , phương trình đường thẳng $O x y z$ đi qua điểm $A (1; 2; 2)$ và vuông góc với mặt phẳng $(P) : 2 x + y - 3 z - 5 = 0$ là

A. $\{\begin{cases} x = 3 + 2 t \\ y = 3 + t \\ z = - 3 - 3 t \end{cases} .$

B. $\{\begin{cases} x = 1 + 2 t \\ y = 2 + t \\ z = 3 t \end{cases} .$

C. $\{\begin{cases} x = 3 + 2 t \\ y = 3 + t \\ z = 3 - 3 t \end{cases} .$

D. $\{\begin{cases} x = 1 + 2 t \\ y = 2 - t \\ z = - 3 t \end{cases} .$

Xem đáp án

Đáp án A
Đường thẳng đi qua điểm

A (1; 2; 0)

và nhận

\vec{n_{P}} = (2; 1; - 3)

là một VTCP

\Rightarrow d : \{\begin{cases} x = 1 + 2 t \\ y = 2 + t \\ z = - 3 t \end{cases} .

Với

t = 1

thì ta được điểm

M (3; 3; - 3)

Thay tọa độ điểm

M (3; 3; - 3)

vào phương trình đường thẳng ở đáp án A nhận thấy thỏa mãn vậy chúng ta chọn đáp án A.

Bắt đầu thi ngay

Bài thi liên quan

Đề số 2
- 53 câu hỏi
- 90 phút
Đề số 3
- 50 câu hỏi
- 90 phút
Đề số 4
- 50 câu hỏi
- 90 phút
Đề số 5
- 50 câu hỏi
- 90 phút
Đề số 6
- 50 câu hỏi
- 90 phút
Đề số 7
- 50 câu hỏi
- 90 phút
Đề số 8
- 50 câu hỏi
- 90 phút
Đề số 9
- 50 câu hỏi
- 90 phút
Đề số 10
- 50 câu hỏi
- 90 phút
Đề số 11
- 50 câu hỏi
- 90 phút

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)

Đề số 1

Danh sách câu hỏi

Bài thi liên quan