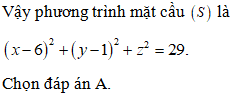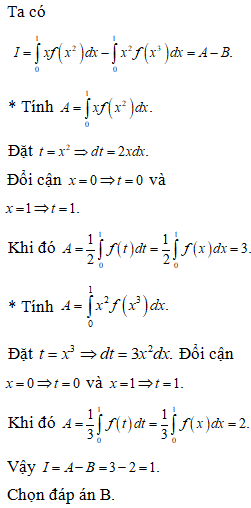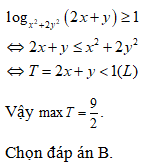Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)
Đề số 28
-
7676 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Số cách chọn ba học sinh từ một nhóm gồm 15 học sinh là
Chọn đáp án D.
Câu 2:
 Xem đáp án
Xem đáp án
Công thức tổng quát của cấp số cộng có số hạng đầu là và công sai d là
Vậy ta có
Chọn đáp án C.
Câu 3:
 Xem đáp án
Xem đáp án
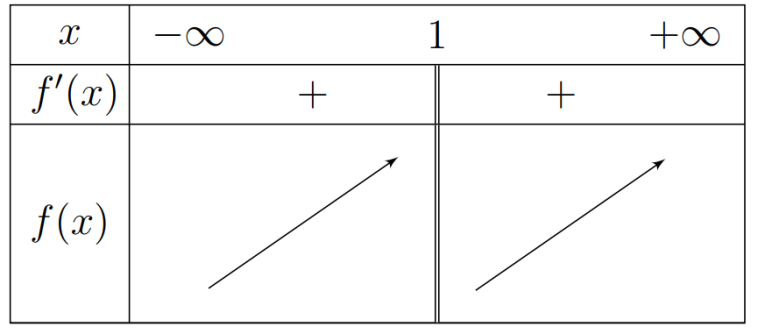
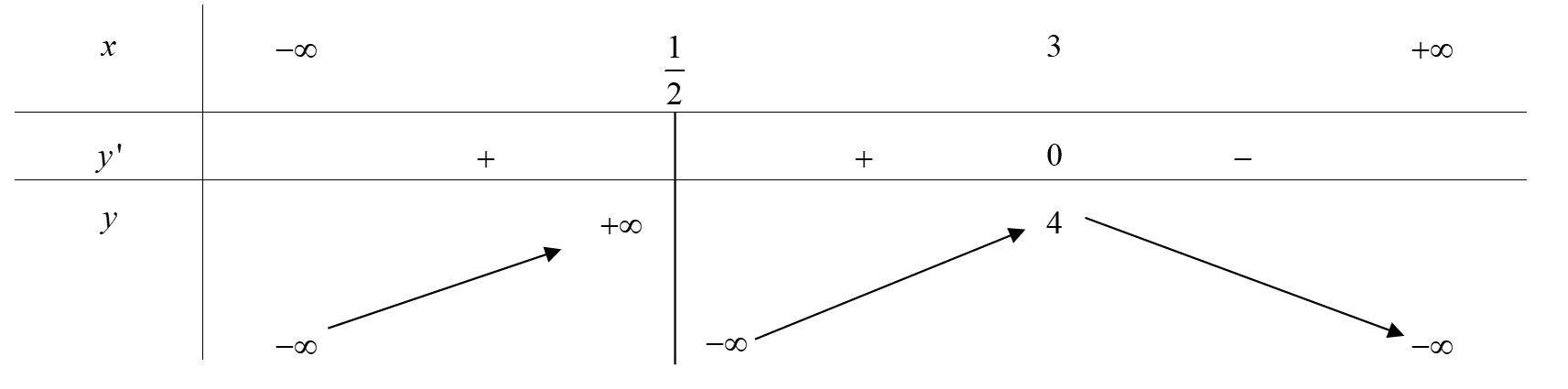
Dựa vào bảng biến thiên, ta thấy hàm số
Đồng biến trên các khoảng
Nghịch biến trên khoảng
Chọn đáp án C.
Câu 4:
 Xem đáp án
Xem đáp án
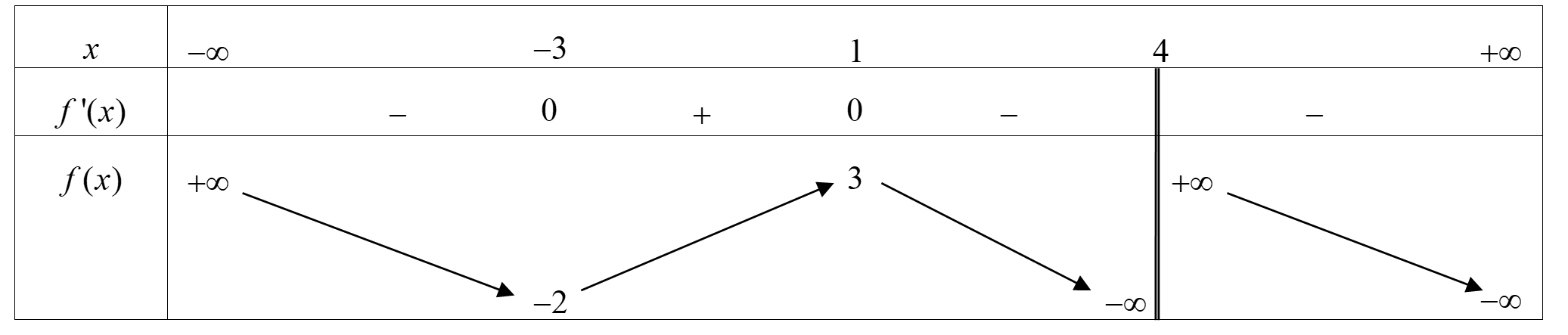
Từ bảng biến thiên, nhận thấy f'(x) đổi dấu từ + sang - tại x=1 do đó hàm số đạt cực đại tại điểm x=1 và Chọn đáp án C.
Câu 5:
 Xem đáp án
Xem đáp án
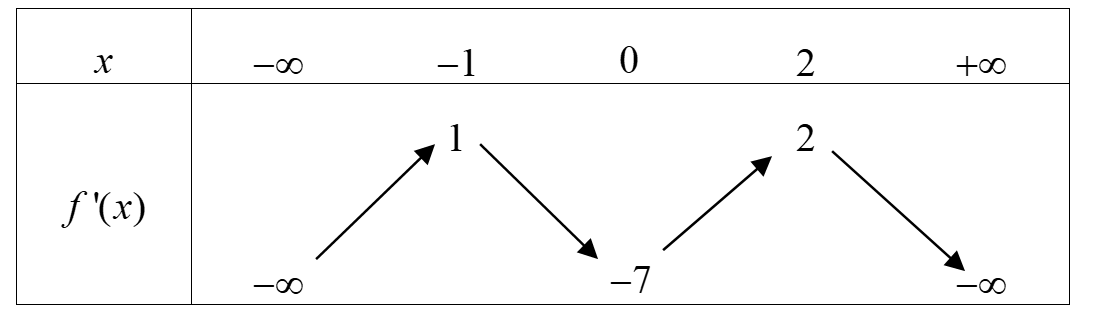
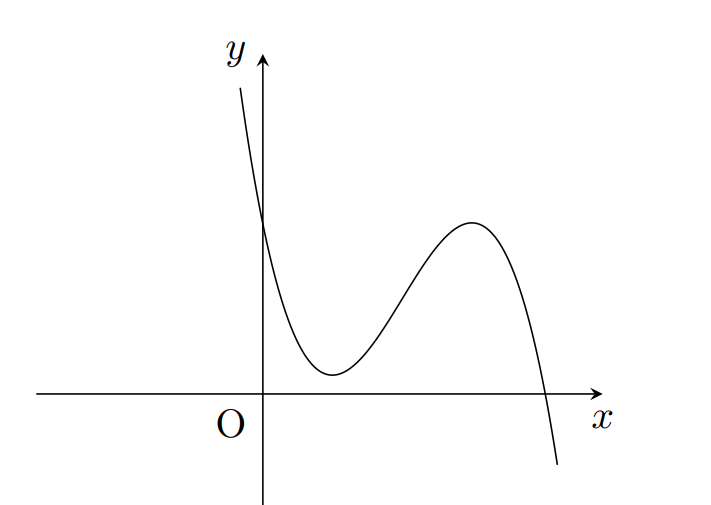
Từ đồ thị hàm số y=f'(x) ta thấy f'(x) đổi dấu một lần (cắt trục Ox tại một điểm) do đó số điểm cực trị của hàm số f(x) là 1.
Chọn đáp án B.Câu 6:
 Xem đáp án
Xem đáp án
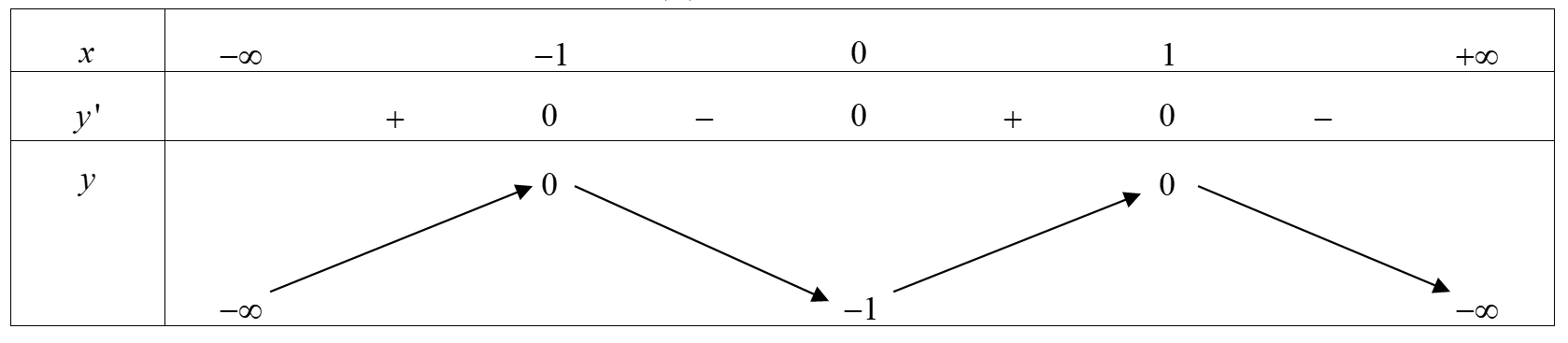
Dựa vào bảng biến thiên, hàm số y=f(x) không có giá trị nhỏ nhất.
Chọn đáp án B.
Câu 7:
 Xem đáp án
Xem đáp án
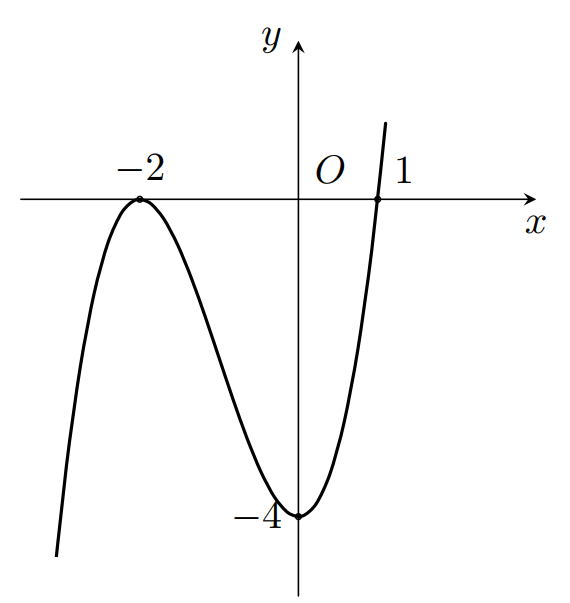
Đồ thị hàm số đi qua điểm (-2;0) nên chọn
Chọn đáp án D.
Câu 8:
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên sau
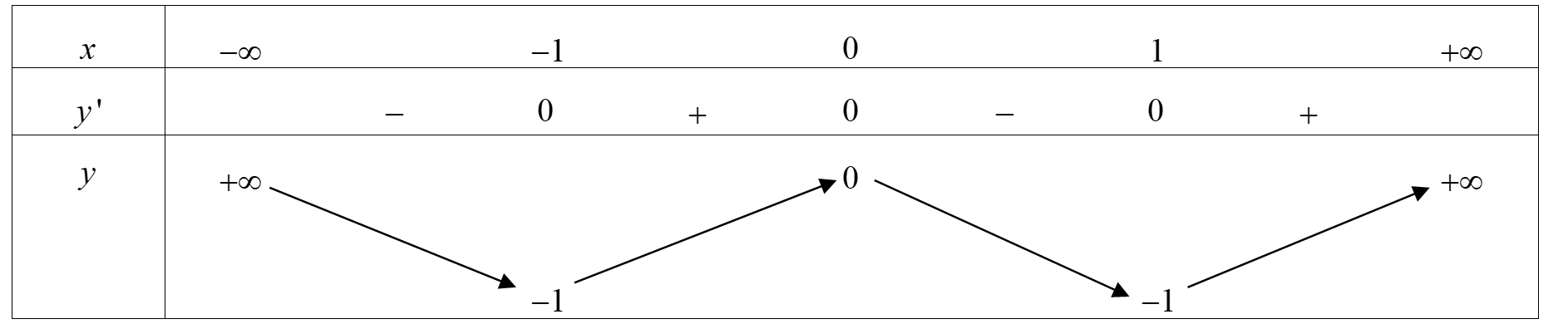
Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-1=m có đúng hai nghiệm.
 Xem đáp án
Xem đáp án
Ta có
Dựa vào bảng biến thiên, phương trình f(x)-1=m có đúng hai nghiệm khi
Chọn đáp án D.
Câu 9:
 Xem đáp án
Xem đáp án
Theo các công thức về logarit.
Chọn đáp án D.Câu 10:
 Xem đáp án
Xem đáp án
Hệ số góc tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x=2 bằng
Chọn đáp án C.
Câu 14:
 Xem đáp án
Xem đáp án
Ta có
Chọn đáp án D.Câu 18:
Cho số phức z=7-5i. Tìm phần thực a của z
 Xem đáp án
Xem đáp án
Số phức z=a+bi với có phần thực là a nên số phức z=7-5i có phần thực là 7.
Chọn đáp án D.Câu 20:
 Xem đáp án
Xem đáp án
Số phức z=-1+2i có điểm biểu diễn M(-1;2)
Chọn đáp án D.Câu 21:
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Câu 22:
 Xem đáp án
Xem đáp án
Thể tích khối lăng trụ là
Chọn đáp án A.
Câu 23:
 Xem đáp án
Xem đáp án
Ta có
Chọn đáp án A.
Câu 24:
 Xem đáp án
Xem đáp án
Khối trụ có chiều cao h, bán kính đáy r có thể tích là
Nên thể tích khối trụ đã cho bằng
Chọn đáp án B.
Câu 26:
Trong không gian với hệ tọa độ Oxyz, tâm I của mặt cầu có tọa độ là
 Xem đáp án
Xem đáp án
Ta có Do đó mặt cầu (S) có tọa độ tâm là
Chọn đáp án A.
Câu 27:
 Xem đáp án
Xem đáp án
Mặt phẳng đi qua điểm M(3;-1;1) và có véc-tơ pháp tuyến có phương trình là
Chọn đáp án D.
Câu 28:
 Xem đáp án
Xem đáp án
Đường thẳng đã cho có véc-tơ chỉ phương và đi qua điểm M(1;0;2) nên có phương trình chính tắc là
Chọn đáp án D.
Câu 29:
 Xem đáp án
Xem đáp án
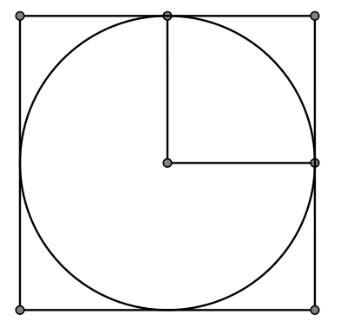
Bán kính đường tròn nội tiếp hình vuông: R=1
Xác suất P chính là tỉ lệ giữa diện tích hình tròn trên diện tích hình vuông.
Do đó:
Chọn đáp án C.
Câu 30:
 Xem đáp án
Xem đáp án
Hàm số đã cho là hàm số trùng phương, có đồ thị đi qua gốc tọa độ.
Chọn đáp án B.
Câu 32:
 Xem đáp án
Xem đáp án
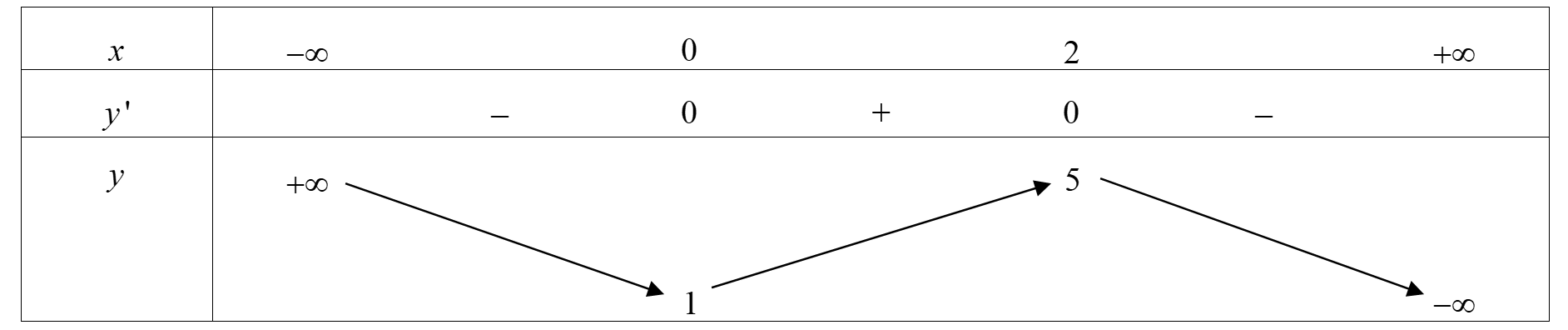
Dựa vào bảng biến thiên, yêu cầu bài toán tương đương với Vậy có 29 giá trị m cần tìm.
Chọn đáp án B.
Câu 38:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Phương trình nào dưới đây là phương trình chính tắc của đường thẳng (d)?
 Xem đáp án
Xem đáp án
Đường thẳng (d) đi qua điểm M(3;-1;0) và nhận làm véc-tơ chỉ phương. Phương trình chính tắc của
Chọn đáp án A.Câu 39:
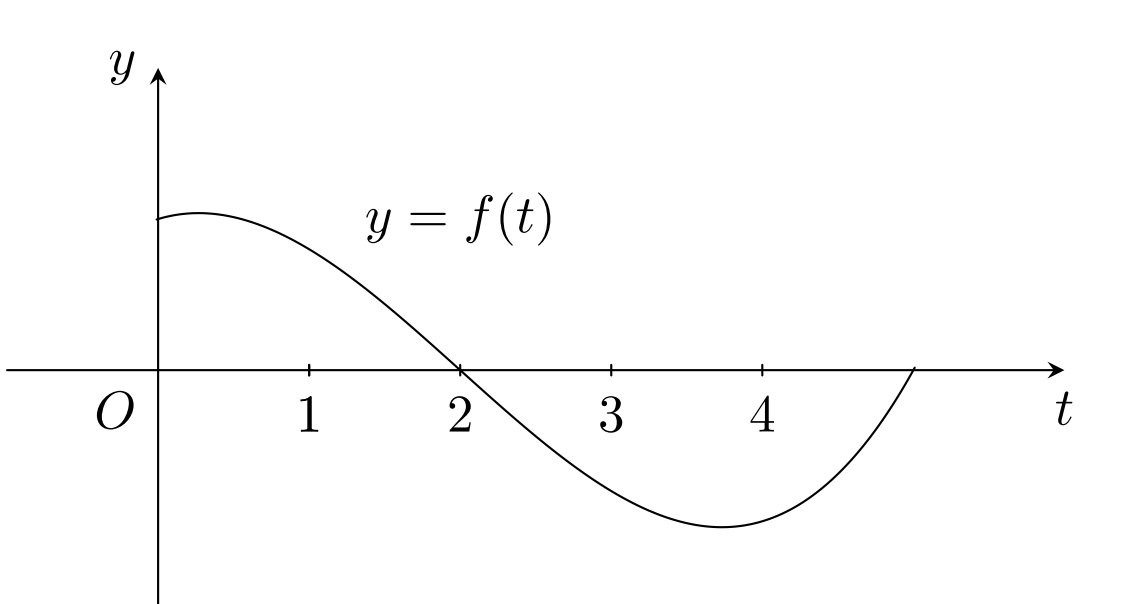
 Xem đáp án
Xem đáp án
Từ đồ thị, ta có bảng biến thiên của hàm số F(x):
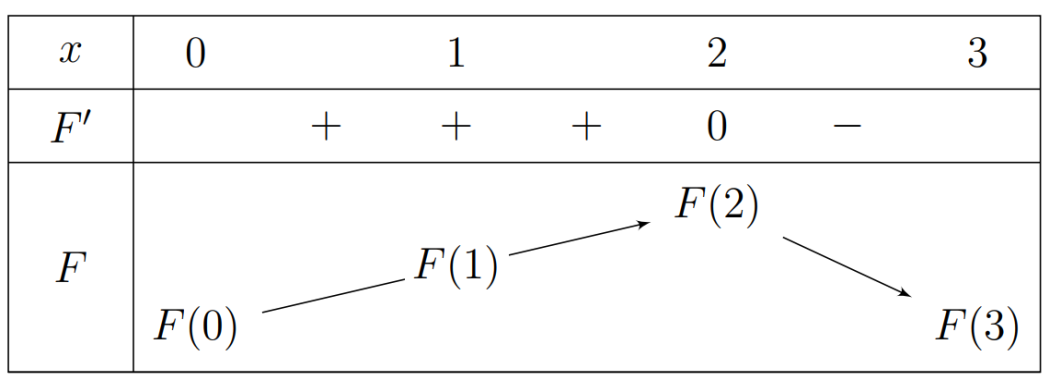
Từ bảng biến thiên suy ra F(2) là giá trị lớn nhất.
Chọn đáp án B.
Câu 40:
 Xem đáp án
Xem đáp án
* Trường hợp 1.
* Trường hợp 2.
Vậy tập hợp các giá trị của x không thỏa mãn bất phương trình là
Chọn đáp án B.Câu 44:
 Xem đáp án
Xem đáp án
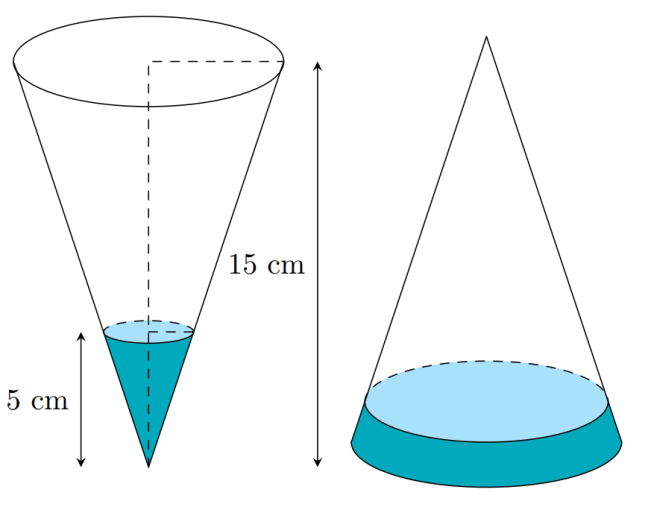
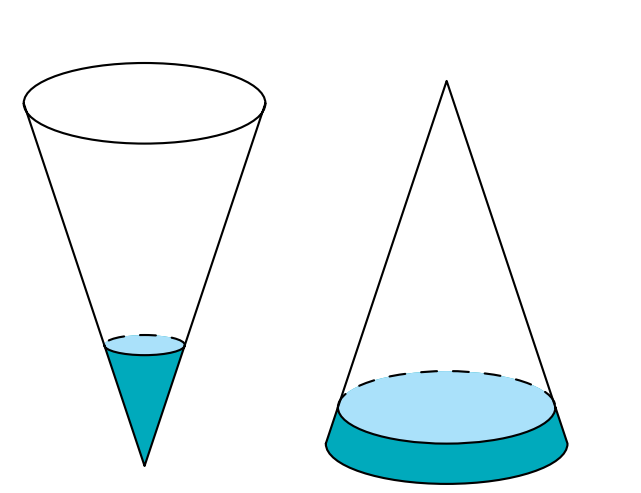
Gọi lần lượt là bán kính đáy, chiều cao và thể tích khối nón được giới hạn bởi phần chứa nước lúc ban đầu; lần lượt là bán kính đáy, chiều cao và thể tích khối nón giới hạn bởi cái phễu; là chiều cao mực nước sau khi lộn ngược phễu. Theo tính chất tam giác đồng dạng ta có:
Sau khi lộn ngược phễu, tỉ số thể tích giữa phần không gian trong phễu không chứa nước và thể tích phễu bằng
Chọn đáp án C.
Câu 48:
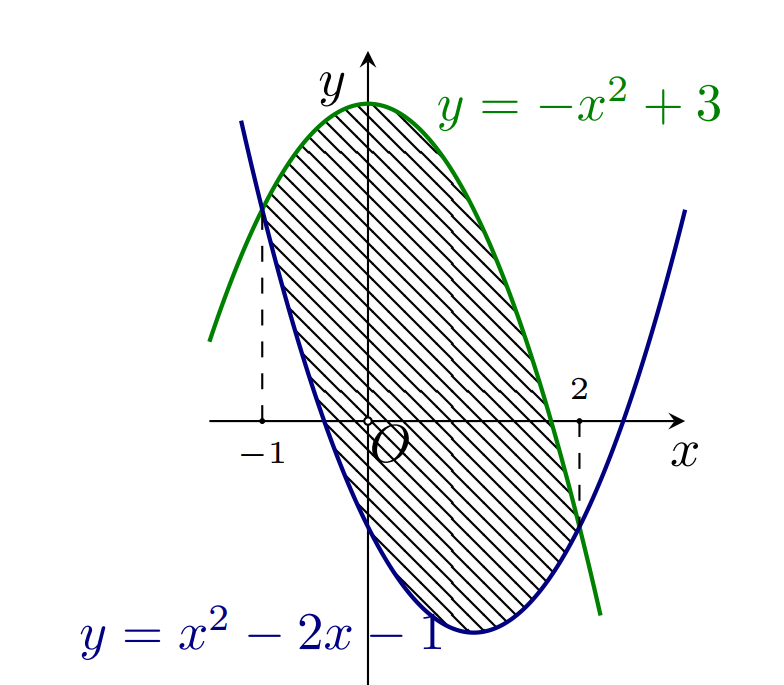
 Xem đáp án
Xem đáp án