50 câu hỏi trắc nghiệm thuộc Đề số 26

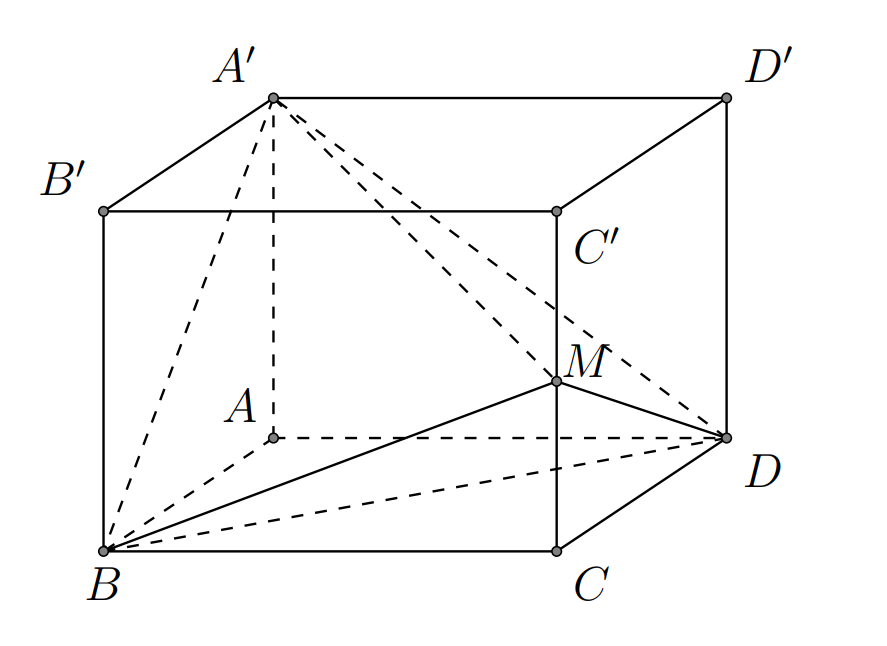
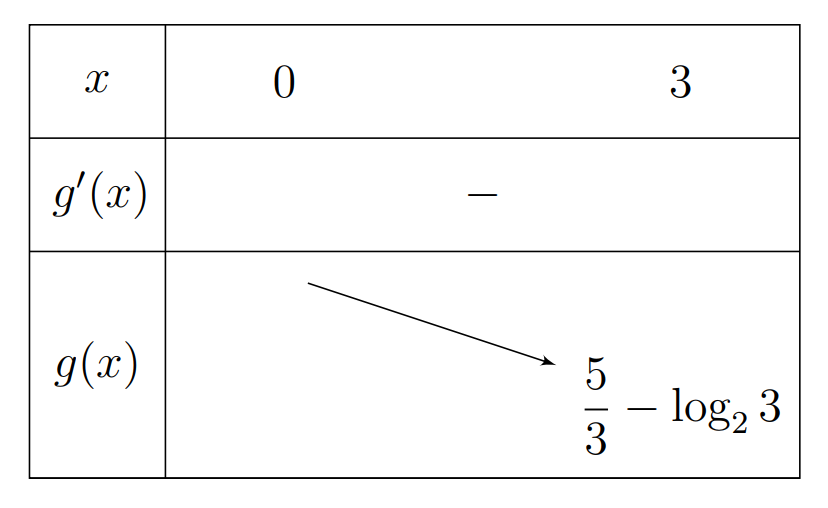
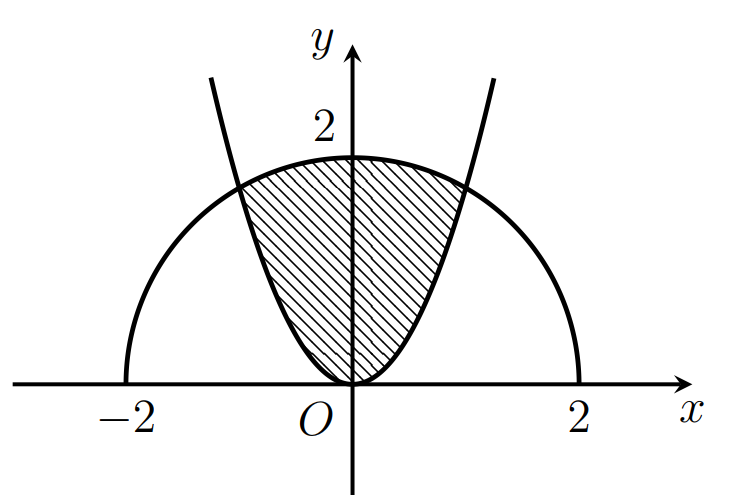
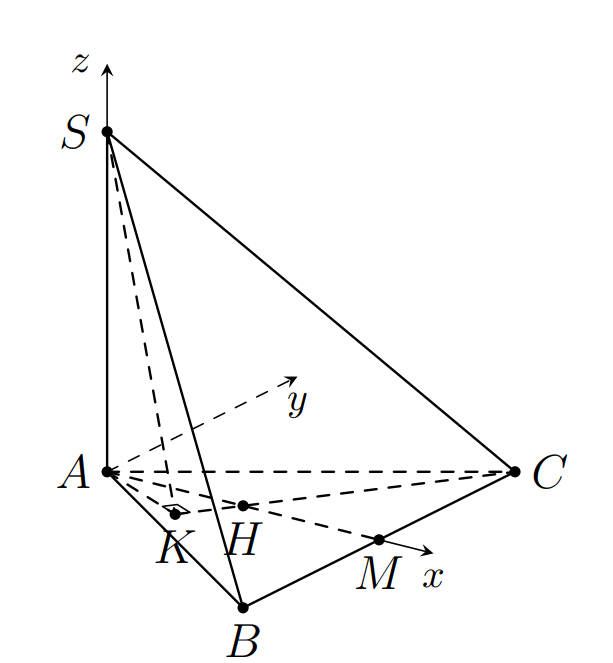
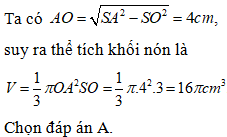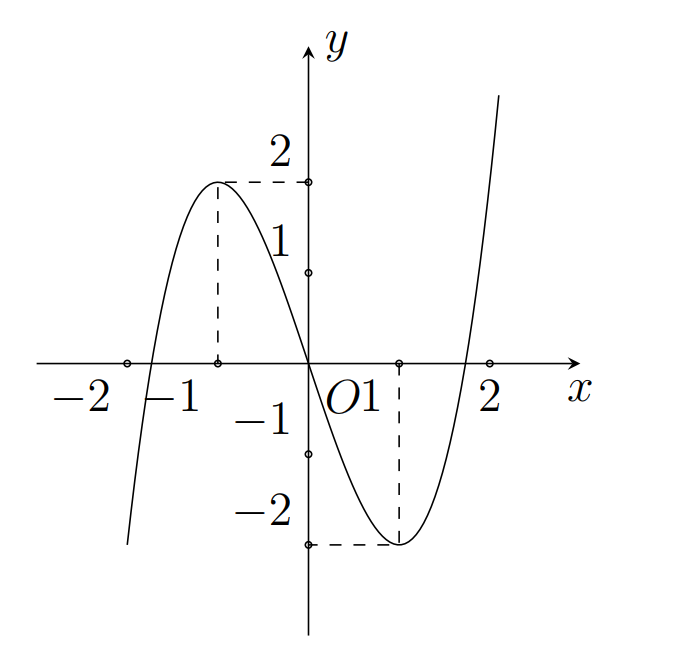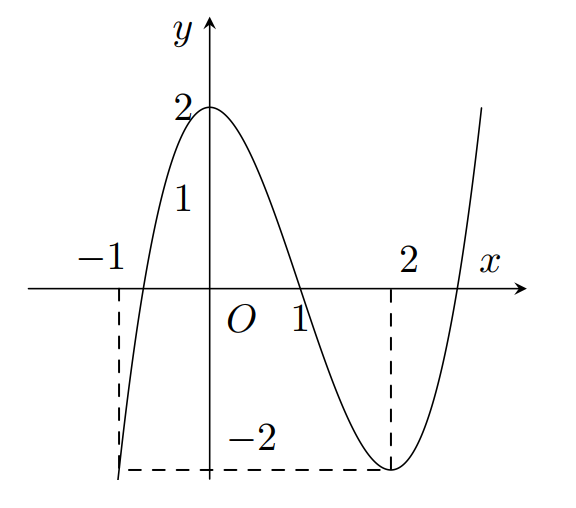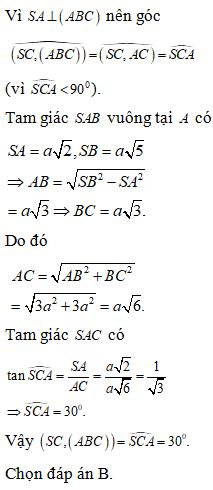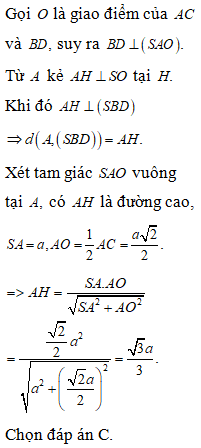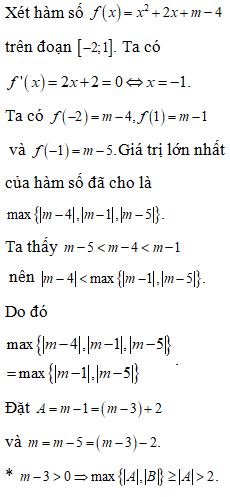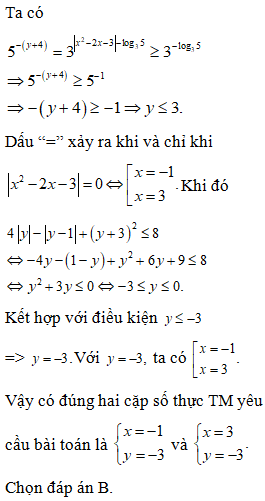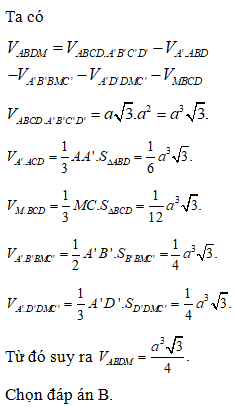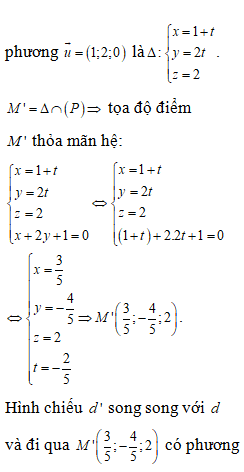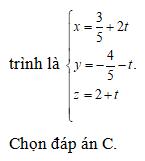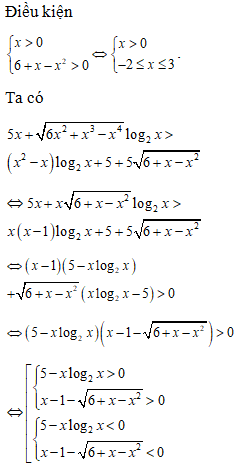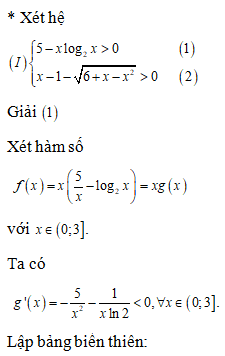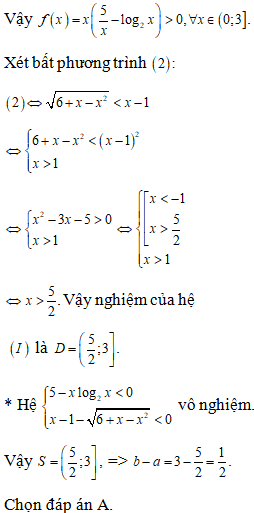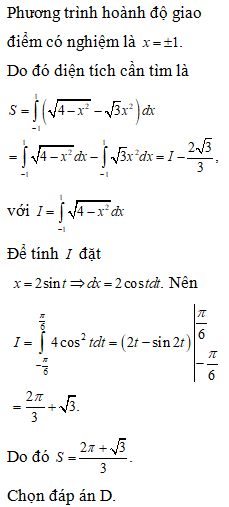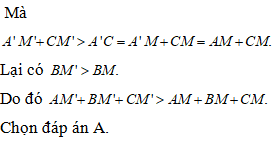Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề số 26

3882 lượt thi
50 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Từ các chữ số 1;2;3;4;5;6;7;8;9 có thể lập được bao nhiêu số tự nhiên có hai chữ số khác nhau?

A. $A_{9}^{2}$

B. $C_{9}^{2}$

C. 2⁹

D. 9²

Xem đáp án

Mỗi cách lập một số tự nhiên có hai chữ số khác nhau từ các chữ số 1;2;3;4;5;6;7;8;9 là một chỉnh hợp chập 2 của 9. Vậy có $A_{9}^{2}$ số tự nhiên có hai chữ số khác nhau

Chọn đáp án A.

Câu 2:

Cho cấp số cộng (u_n) với u₁=2 và công sai d=1. Khi đó

u₃bằng

A. 3

B. 1

C. 4

D. 2

Xem đáp án

Ta có $u_{3} = u_{1} + 2 d = 2 + 2.1 = 4.$

Chọn đáp án C.

Câu 3:

Cho hàm số y=f(x) có đồ thị như hình vẽ dưới đây. Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?

A. (-1;2)

B. (0;2)

C. $(- \infty; 0)$

D. $(2; + \infty)$

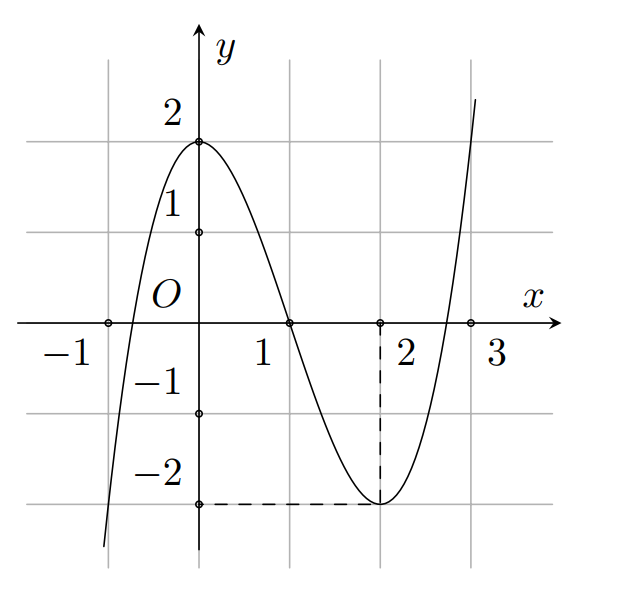
Xem đáp án

Trên khoảng (0;2) đồ thị hàm số y=f(x) đi xuống từ trái sang phải nên hàm số y=f(x) nghịch biến trên (0;2).

Chọn đáp án B.

Câu 4:

Cho hàm số y=f(x) có đạo hàm trên R và có bảng xét dấu y' như sau

Hàm số y=f(x) đạt cực đại tại điểm

A. x = 2

B. x = 2 và x = -2

C. x = -2

D. x = 0

Xem đáp án

Hàm số đạt cực đại tại điểm khi đi qua nó đạo hàm đổi dấu từ dương sang âm.

Dựa vào bảng xét dấu của đạo hàm ta có hàm số đạt cực đại tại điểm x=0

Chọn đáp án D.

Câu 5:

Cho hàm số có đồ thị y=f(x) như hình vẽ bên dưới. Trên đoạn [-3;1] hàm số đã cho có mấy điểm cực trị?

A. 1

B. 2

C. 3

D. 4

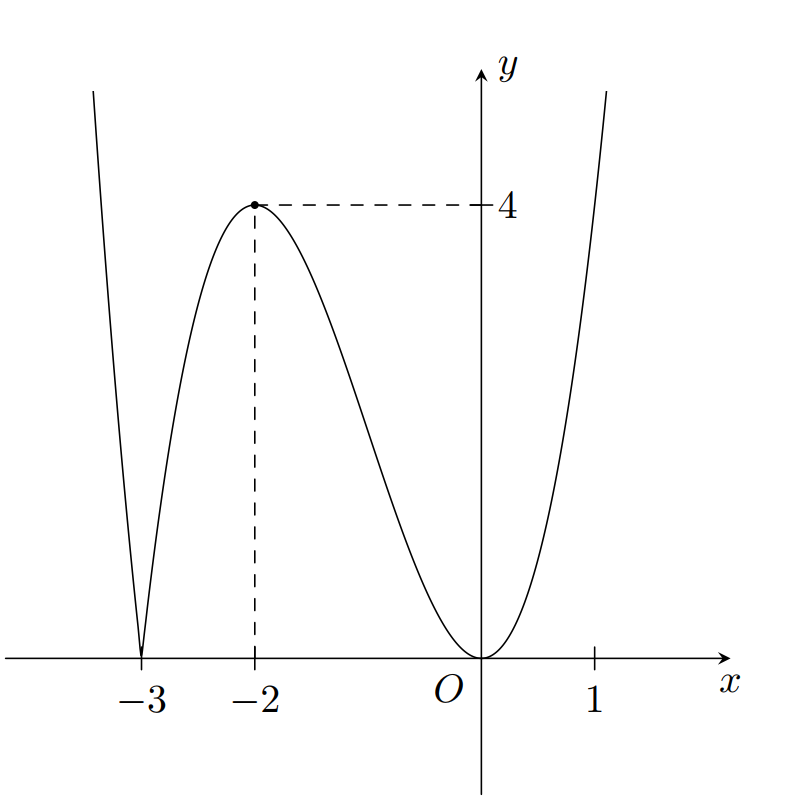
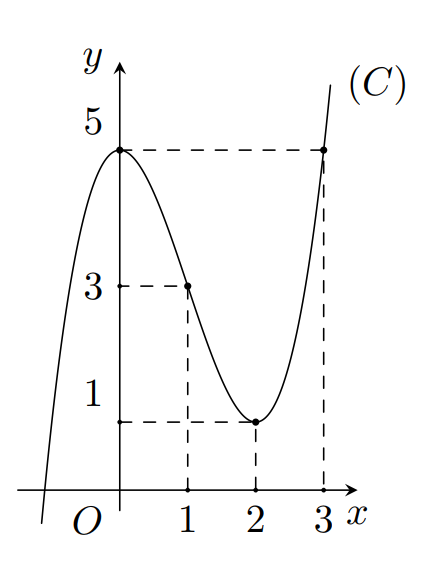
Xem đáp án

Dựa vào đồ thị ta thấy, trên đoạn [-3;1] hàm số đã cho có 2 điểm cực trị.

Nhận xét: Câu này rất dễ đánh lừa học sinh vì đọc lướt nhanh và nhìn đồ thị học sinh ngộ nhận tại x=-3 hàm số cũng có cực trị

Chọn đáp án B.

Câu 6:

Cho hàm số

y = \frac{2}{x - 5} .

Tìm đường tiệm cận ngang của đồ thị hàm số.

A. $y = - \frac{2}{5} .$

B. y = 2.

C. y = 0.

D. x = 5.

Xem đáp án

Ta có $\lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{2}{x - 5} = 0 và \lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{2}{x - 5} = 0$ và nên đường thẳng y=0 là tiệm cận ngang của đồ thị hàm số.

Chọn đáp án C

Câu 7:

Đường cong hình bên là đồ thị của hàm số

y = a x^{4} + b x^{2} + c

với a,b,c là các số thực. Mệnh đề nào dưới đây đúng?

A. $a < 0; b > 0; c < 0.$

B. $a > 0; b > 0; c < 0.$

C. $a > 0; b < 0; c < 0$

D. $a < 0; b < 0; c > 0$

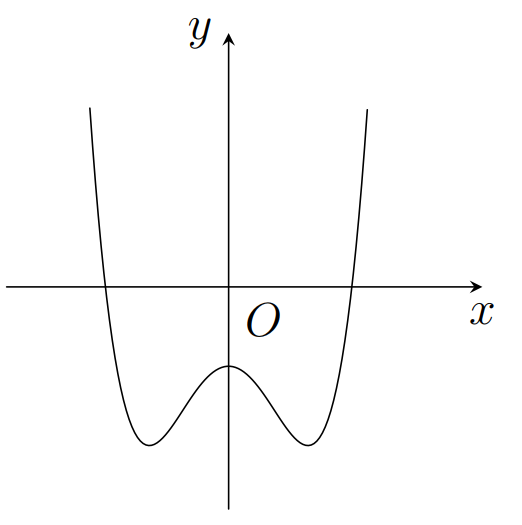
Xem đáp án

Quan sát đồ thị, ta thấy $\lim_{x \to \infty} y = + \infty \Rightarrow a > 0.$

Mặt khác, đồ thị hàm số có ba điểm cực trị nên b,a khác dấu, kết hợp với a>0 ta được b<0

Đồ thị hàm số cắt trục tung tại điểm có hoành độ âm nên c=y(0)<0

Chọn đáp án C.

Câu 8:

Cho hàm số

y = (x - 2) (x^{2} + 1)

có đồ thị (C) Mệnh đề nào sau đây đúng?

A. (C) cắt trục hoành tại hai điểm.

B. (C) cắt trục hoành tại một điểm.

C. (C) không cắt trục hoành.

D. (C) cắt trục hoành tại ba điểm.

Xem đáp án

$(C) \cap O x \Leftrightarrow y = 0 \Leftrightarrow x = 2$

Chọn đáp án B.

Câu 9:

Với các số thực dương a,b bất kì. Mệnh đề nào dưới đây đúng?

A. $\ln (a b) = \ln a + \ln b .$

B. $\ln (a b) = \ln a . \ln b .$

C. $\ln \frac{a}{b} = \frac{\ln a}{\ln b} .$

D. $\ln \frac{a}{b} = \ln b - \ln a .$

Xem đáp án

Với mọi số dương a,b ta có: $\ln (a b) = \ln a + \ln b .$

Chọn đáp án A.

Câu 10:

Đạo hàm của hàm số $y = 3^{x}$ là

A. $y' = 3^{x} \ln 3.$

B. $y' = \frac{3^{x}}{\ln 3} .$

C. $y' = x 3^{x - 1} .$

D. $y' = 3^{x} .$

Xem đáp án

Áp dụng công thức tính đạo hàm của hàm số mũ, ta có $(3^{x})' = 3^{x} \ln 3.$

Chọn đáp án A.

Câu 11:

Cho các số thực m,n và a là số thực dương. Mệnh đề nào sau đây là mệnh đề đúng?

A. $a^{m + n} = {(a^{m})}^{n} .$

B. $a^{m + n} = \frac{a^{m}}{a^{n}}$ .

C. $a^{m + n} = a^{m} . a^{n} .$

D. $a^{m + n} = a^{m} + n .$

Xem đáp án

Ta có $a^{m + n} = a^{m} . a^{n} .$

Chọn đáp án C.

Câu 12:

Tìm tập nghiệm S của phương trình

3^{x^{2}} = 9.

A. $S = \{\sqrt{2}; 2\}$ .

B. $S = \{- \sqrt{2}; \sqrt{2}\}$ .

C. $S = \{- \sqrt{2}; 2\}$ .

D. $S = \{- 2; 2\} .$

Xem đáp án

PT $\Leftrightarrow 3^{x^{2}} = 3^{2} \Leftrightarrow x^{2} = 2 \Leftrightarrow x = \pm \sqrt{2} .$

Chọn đáp án B.

Câu 13:

Phương trình

\log_{2} (x - 3) = 3

có nghiệm là

A. x = 5

B. x = 12

C. x = 9

D. x = 11

Xem đáp án

Phương trình $\log_{2} (x - 3) = 3 \Leftrightarrow x - 3 = 2^{3} \Leftrightarrow x = 11.$

Chọn đáp án D.

Câu 14:

Tìm nguyên hàm của hàm số

f (x) = 2 x^{3} - 9.

A. $\int_{}^{} f (x) d x = \frac{1}{2} x^{4} - 9 x + C .$

B. $\int_{}^{} f (x) d x = x^{4} - 9 x + C .$

C. $\int_{}^{} f (x) d x = \frac{1}{2} x^{4} + C .$

D. $\int_{}^{} f (x) d x = 4 x^{3} + 9 x + C .$

Xem đáp án

$\int_{}^{} (2 x^{3} - 9) d x = \frac{1}{2} x^{4} - 9 x + C .$

Chọn đáp án A.

Câu 15:

Họ nguyên hàm của hàm số

f (x) = e^{2 x} + x^{2}

là

A. $F (x) = \frac{e^{2 x}}{2} + \frac{x^{3}}{3} + C .$

B. $F (x) = e^{2 x} + x^{3} + C .$

C. $F (x) = 2 e^{2 x} + 2 x + C .$

D. $F (x) = e^{2 x} + \frac{x^{3}}{3} + C .$

Xem đáp án

Ta có $\int_{}^{} (e^{2 x} + x^{2}) d x = \frac{e^{2 x}}{2} + \frac{x^{3}}{3} + C .$

Chọn đáp án A.

Câu 16:

Biết

\int_{a}^{b} f (x) d x = 10, F (x)

là một nguyên hàm của f(x) và F(a)=-3. Tính F(b)

A. F(b) = 13.

B. F(b) = 10.

C. F(b) = 16.

D. F(b) = 7.

Xem đáp án

Ta có: $\int_{a}^{b} f (x) d x = 10 \Leftrightarrow F (b) - F (a) = 10 \Leftrightarrow F (b) = 7.$

Chọn đáp án D.

Câu 17:

Cho

\int_{2}^{5} f (x) d x = 10.

Khi đó

\int_{5}^{2} [2 - 4 f (x)] d x

bằng

A. 32

B. 34

C. 42

D. 46

Xem đáp án

Ta có

$\int_{5}^{2} [2 - 4 f (x)] d x = \int_{5}^{2} 2 d x - 4 \int_{5}^{2} f (x) d x = 2 (2 - 5) - 4. (- 10) = 34.$

Chọn đáp án B.

Câu 18:

Cho số phức

z = 7 - i \sqrt{5}

. Phần thực và phần ảo của số phức

\bar{z}

lần lượt là

A. 7 và $\sqrt{5}$

B. -7 và $\sqrt{5}$

C. 7 và $i \sqrt{5}$

D. 7 và $- \sqrt{5}$

Xem đáp án

Có $\bar{z} = 7 + i \sqrt{5},$ có phần thực là 7, phần ảo là $\sqrt{5}$ .

Chọn đáp án A.

Câu 19:

Cho hai số phức

z_{1} = 2 - 2 i, z_{2} = - 3 + 3 i .

Khi đó số phức

z_{1} - z_{2}

là

A. -5 + 5i

B. -5i

C. 5 - 5i

D. -1 + i

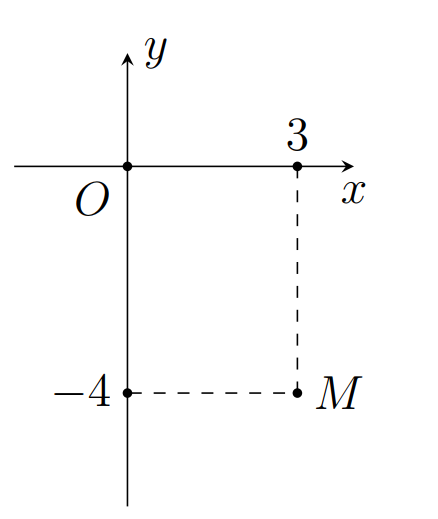
Xem đáp án

Ta có $z_{1} - z_{2} = (2 - 2 i) - (- 3 + 3 i) = 5 - 5 i .$

Chọn đáp án C.

Câu 20:

Trên mặt phẳng tọa độ Oxyz cho điểm M trong hình vẽ bên là điểm biễu diễn của số phức z. Tìm z

A. z = -4 + 3i

B. z = -3 + 4i

C. z = 3 - 4i

D. z = 3 + 4i

Xem đáp án

Điểm M có tọa độ là M(3;-4) => điểm M biểu diễn số phức z=3-4i

Chọn đáp án C.

Câu 21:

Tính thể tích V của khối hộp có chiều cao bằng h và diện tích đáy bằng B.

A. $V = \frac{1}{3} B . h$

B. V = B.h

C. $V = \frac{1}{2} B . h$

D. $V = \frac{1}{6} B . h$

Xem đáp án

Thể tích khối hộp là V=B.h

Chọn đáp án B.

Câu 22:

Cho hình lăng trụ tam giác đều ABC.A'B'C' có

A B = 2 a, A A' = a \sqrt{3} .

Tính thể tích khối lăng trụ ABC.A'B'C'.

A. $3 a^{3} .$

B. $a^{3} .$

C. $\frac{a^{3}}{4} .$

D. $\frac{3 a^{3}}{4} .$

Xem đáp án

Câu 23:

Một khối trụ có bán kính đáy R đường cao h. Thể tích khối trụ bằng

A. $V = π R^{2} h$

B. $\frac{1}{3} π R^{2} h .$

C. $2 π R^{2} h .$

D. $2 π R h .$

Xem đáp án

Thể tích khối trụ là $V = π R^{2} h$

Chọn đáp án A.

Câu 24:

Cho tam giác SOA vuông tại O có

S O = 3 c m, S A = 5 c m .

Quay tam giác SOA xung quanh cạnh SO được khối nón. Thể tích khối nón tương ứng là

A. $16 π c m^{3} .$

B. $36 π c m^{3} .$

C. $15 π c m^{3} .$

D. $\frac{80 π}{3} π c m^{3} .$

Xem đáp án

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $M (- 1; 2; 3), N (0; 2; - 1) .$ Tọa độ trọng tâm của tam giác OMN là

A. $(- \frac{1}{3}; \frac{4}{3}; \frac{2}{3}) .$

B. $(- \frac{1}{2}; 2; 1) .$

C. (1;0;-4).

D. (-1;4;2).

Xem đáp án

Tọa độ trọng tâm của tam giác OMN là $(\frac{- 1 + 0 + 0}{3}; \frac{2 + 2 + 0}{3}; \frac{3 + (- 1) + 0}{3}) = (- \frac{1}{3}; \frac{4}{3}; \frac{2}{3}) .$

Chọn đáp án A.

Câu 26:

Viết phương trình mặt cầu tâm I(1;-2;3) và bán kính R=2.

A. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 4.$

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 4.$

C. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 2 .$

D. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 2 .$

Xem đáp án

Mặt cầu tâm I(1;-2;3) và bán kính R=2 có phương trình là ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 4.$

Chọn đáp án A.

Câu 27:

Trong không gian với hệ tọa độ Oxyz cho ba điểm $A (1; 0; 0), B (0; - 2; 0), C (0; 0; 3) .$ Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)?

A. $\frac{x}{3} + \frac{y}{1} + \frac{z}{- 2} = 1.$

B. $\frac{x}{1} + \frac{y}{- 2} + \frac{z}{3} = 0.$

C. $\frac{x}{- 2} + \frac{y}{1} + \frac{z}{3} = 1.$

D. $\frac{x}{1} + \frac{y}{- 2} + \frac{z}{3} = 1$ .

Xem đáp án

Phương trình mặt phẳng (ABC) là $\frac{x}{1} + \frac{y}{- 2} + \frac{z}{3} = 1$ (phương trình mặt phẳng theo đoạn chắn).

Chọn đáp án D.

Câu 28:

Trong không gian Oxyz, cho hai điểm A(2;-1;4) và B(-1;3;2). Đường thẳng AB có một véc-tơ chỉ phương là

A. $\vec{m} (1; - 4; 2) .$

B. $\vec{u} (1; 2; 2)$ .

C. $\vec{v} (- 3; 4; - 2) .$

D. $\vec{n} (1; 2; 6)$ .

Xem đáp án

$\vec{A B} = (- 3; 4; - 2) .$ Vậy đường thẳng AB có một véc-tơ chỉ phương là $\vec{v} (- 3; 4; - 2) .$

Chọn đáp án C.

Câu 29:

Có 16 tấm bìa ghi 16 chữ “HỌC”, “ĐỂ”, “BIẾT”, “HỌC”, “ĐỂ”, “LÀM”, “HỌC”, “ĐỂ”, “CHUNG”, “SỐNG”, “HỌC”, “ĐỀ”, “TỰ”, “KHẲNG”, “ĐỊNH”, “MÌNH”. Một người xếp ngẫu nhiên 16 tấm bìa cạnh nhau. Tính xác suất để xếp các tấm bìa được dòng chữ “HỌC ĐỀ BIẾT HỌC ĐỂ LÀM HỌC ĐỂ CHUNG SỐNG HỌC ĐỂ TỰ KHẲNG ĐỊNH MÌNH

A. $\frac{8}{16!}$

B. $\frac{4!}{16!}$

C. $\frac{1}{16!}$

D. $\frac{4! .4!}{16!}$

Xem đáp án

Câu 30:

Cho hàm số y=f(x) có đồ thị như hình bên. Khi đó y=f(x) là hàm số nào sau đây?

A. $y = x^{3} - 3 x .$

B. $y = - x^{3} + 3 x$

C. $y = x^{3} + x^{2} - 4.$

D. $y = x^{3} - 3 x + 1.$

Xem đáp án

Câu 31:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0;1].

A. $\max_{[0; 1]} y = 2, \min_{[0; 1]} y = 1.$

B. $\max_{[0; 1]} y = 0, \min_{[0; 1]} y = - 2.$

C. $\max_{[0; 1]} y = 2, \min_{[0; 1]} y = - 2.$

D. $\max_{[0; 1]} y = 2, \min_{[0; 1]} y = 0.$

Xem đáp án

Câu 32:

Tập nghiệm của bất phương trình

3^{x} > 9

là

A. $(2; + \infty)$

B. (0;2)

C. $(0; + \infty)$

D. $(- 2; + \infty)$

Xem đáp án

Ta có $3^{x} > 9 \Leftrightarrow 3^{x} > 3^{2} \Leftrightarrow x > 2.$

Chọn đáp án A.

Câu 33:

Tính tích phân

I = \int_{0}^{\frac{π}{4}} \cos (\frac{π}{2} - x) d x .

A. $I = \frac{1 - \sqrt{2}}{\sqrt{2}}$ .

B. $I = 1 - \sqrt{2} .$

C. $I = \frac{\sqrt{2} - 1}{\sqrt{2}} .$

D. $I = \sqrt{2} - 1.$

Xem đáp án

Ta có

$I = \int_{0}^{\frac{π}{4}} \cos (\frac{π}{2} - x) d x = \int_{0}^{\frac{π}{4}} \sin x d x = - \cos x |\begin{array}{l} \frac{π}{4} \\ 0 \end{array} = 1 - \frac{\sqrt{2}}{2} = \frac{\sqrt{2} - 1}{\sqrt{2}} .$

Chọn đáp án C.

Câu 34:

Cho hai số phức

z_{1} = 1 + 2 i v à z_{2} = 2 - 3 i .

Phần ảo của số phức

w = 3 z_{1} - 2 z_{2}

là

A. 12

B. 1

C. 11

D. 12i

Xem đáp án

$w = 3 z_{1} - 2 z_{2} = - 1 + 12 i .$ Vậy w có phần ảo là 12.

Chọn đáp án A.

Câu 35:

Cho hình chóp S.ABC có SA vuông góc với đáy ABC. Tam giác ABC vuông cân tại B và

S A = a \sqrt{2}, S B = a \sqrt{5} .

Tính góc giữa SC và mặt phẳng (ABC).

A. $45^{0}$

B. $30^{0}$

C. $120^{0}$

D. $60^{0}$

Xem đáp án

Câu 36:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh

a, S A ⊥ (A B C D)

và SA=a. Khoảng cách từ điểm A đến mặt phẳng (SBD) bằng

A. $\frac{a}{2} .$

B. $\frac{a \sqrt{6}}{3} .$

C. $\frac{a \sqrt{3}}{3} .$

D. $\frac{a \sqrt{2}}{2} .$

Xem đáp án

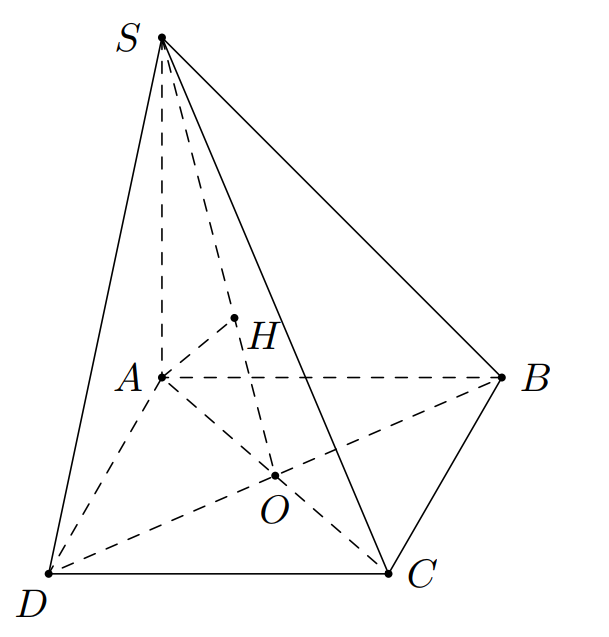
Câu 37:

Trong không gian Oxyz cho mặt cầu (S) có tâm I(1;1;1). Một mặt phẳng (P) cắt (S) theo giao tuyến là một đường tròn (C). Biết chu vi lớn nhất của (C) bằng $2 π \sqrt{2} .$ Phương trình của (S) là

A. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 4 .$

B. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 2$ .

C. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 4 .$

D. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 2.$

Xem đáp án

Đường tròn (C) đạt chu vi lớn nhất khi (C) đi qua tâm I của mặt cầu (S)

Ta có: $C = 2 π R = 2 π \sqrt{2} \Leftrightarrow R = \sqrt{2} .$

Khi đó

$\Rightarrow (S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 2.$

Chọn đáp án D.

Câu 38:

Trong không gian Oxyz, cho A(1;-2;1) và B(0;1;3) Phương trình đường thẳng đi qua hai điểm A,B là

A. $\frac{x + 1}{- 1} = \frac{y - 3}{- 2} = \frac{z - 2}{1} .$

B. $\frac{x}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{2} .$

C. $\frac{x + 1}{- 1} = \frac{y - 2}{3} = \frac{z + 1}{2} .$

D. $\frac{x}{1} = \frac{y - 1}{- 2} = \frac{z - 3}{1} .$

Xem đáp án

Ta có $\vec{A B} = (- 1; 3; 2) .$

Đường thẳng AB có phương trình chính tắc là $\frac{x}{- 1} = \frac{y - 1}{3} = \frac{z - 3}{2} .$

Chọn đáp án B.

Câu 39:

Tìm tất cả các giá trị của tham số m để giá trị lớn nhất của hàm số

y = |x^{2} + 2 x + m - 4|

trên đoạn [-2;1] đạt giá trị nhỏ nhất. Giá trị của m là

A. 5

B. 4

C. 1

D. 3

Xem đáp án

Câu 40:

Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện

3^{|x^{2} - 2 x - 3| - \log_{3} 5} = 5^{- (y + 4)} và 4 |y| - |y - 1| + {(y + 3)}^{2} \leq 8.

A. 3

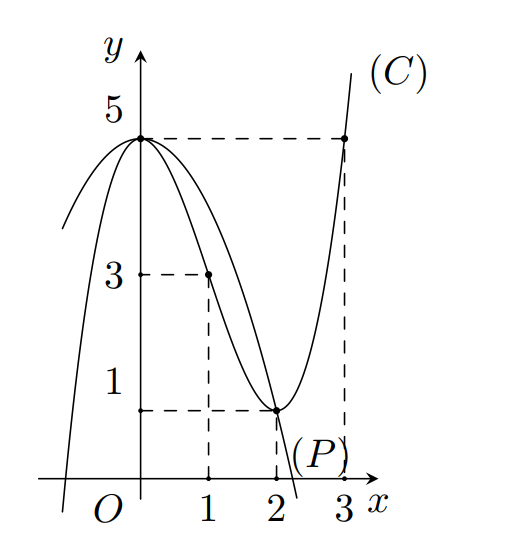
B. 2

C. 1

D. 4

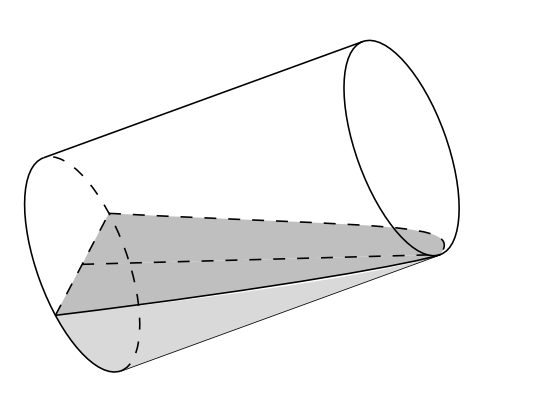
Xem đáp án

Câu 41:

Biết $\int_{0}^{1} \frac{x^{3} + 3 x}{x^{2} + 3 x + 2} d x = a + b \ln 2 + c \ln 3$ với a,b,c là các số hữu tỉ, tính $S = 2 a + b^{2} + c^{2} .$

A. S = 515

B. S = 164

C. S = 436

D. S = -9

Xem đáp án

Ta có $\int_{0}^{1} \frac{x^{3} + 3 x}{x^{2} + 3 x + 2} d x = \int_{0}^{1} (x - 3 - \frac{4}{x + 1} + \frac{14}{x + 2}) d x = (\frac{x^{2}}{2} - 3 x - 4 \ln |x + 1| + 14 \ln |x + 2|) |\begin{array}{l} 1 \\ 0 \end{array} = - \frac{5}{2} - 18 \ln 2 + 14 \ln 3.$

Vậy $a = - \frac{5}{2}, b = - 18, c = 14.$ Khi đó tổng $S = 2 a + b^{2} + c^{2} = 515.$

Chọn đáp án A.

Câu 42:

Cho số phức

z = a + b i (a, b \in ℝ, a < 0)

thỏa mãn

1 + \bar{z} = {|\bar{z} - i|}^{2} + {(i z - 1)}^{2} .

Tính |z|

A. $\frac{\sqrt{2}}{2} .$

B. $\sqrt{5} .$

C. $\frac{\sqrt{17}}{2} .$

D. $\frac{1}{2} .$

Xem đáp án

Câu 43:

Cho hình hình hộp chữ nhật ABCD.A'B'C'D'có đáy là hình vuông cạnh a chiều cao

A A' = a \sqrt{3} .

Gọi M là trung điểm của CC'. Tính thể tích của khối tứ diện BDA'M

A. $\frac{a^{3} \sqrt{3}}{6} .$

B. $\frac{a^{3} \sqrt{3}}{4} .$

C. $\frac{a^{3} \sqrt{3}}{15} .$

D. $\frac{a^{3} \sqrt{3}}{12} .$

Xem đáp án

Câu 44:

Một chiếc cốc hình trụ có đường kính đáy 6 cm, chiều cao 15 cm chứa đầy nước. Nghiêng cốc cho nước chảy từ từ ra ngoài cho đến khi mép nước ngang với đường kính của đáy. Khi đó diện tích của bề mặt nước trong cốc bằng.

A. $9 \sqrt{26 π} c m^{2} .$

B. $\frac{9 \sqrt{26} π}{2} c m^{2} .$

C. $\frac{9 \sqrt{26} π}{5} c m^{2} .$

D. $\frac{9 \sqrt{26} π}{10} c m^{2} .$

Xem đáp án

Đáp án B

Câu 45:

Trong không gian Oxyz, cho đường thẳng

d : \{\begin{cases} x = 1 + 2 t \\ y = - t \\ z = 2 + t \end{cases}

và mặt phẳng (P): x+2y+1=0. Tìm hình chiếu của đường thẳng d trên (P)

A. $\{\begin{cases} x = \frac{19}{5} + 2 t \\ y = - \frac{2}{5} - t \\ z = t \end{cases} .$

B. $\{\begin{cases} x = \frac{19}{5} + 2 t \\ y = - \frac{12}{5} - t \\ z = 1 + t \end{cases} .$

C. $\{\begin{cases} x = \frac{3}{5} + 2 t \\ y = - \frac{4}{5} - t \\ z = 2 + t \end{cases} .$

D. $\{\begin{cases} x = \frac{1}{5} + 2 t \\ y = - \frac{2}{5} - t \\ z = 1 + t \end{cases} .$

Xem đáp án

Câu 46:

Cho hàm số y=f(x). Đồ thị hàm số y=f'(x) như hình vẽ bên. Số điểm cực trị của hàm số

g (x) = 3 f (x) + x^{3} - 15 x + 1

là

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Câu 47:

Giả sử S=(a;b] là tập nghiệm của bất phương trình $5 x + \sqrt{6 x^{2} + x^{3} - x^{4}} \log_{2} x > (x^{2} - x) \log_{2} x + 5 + 5 \sqrt{6 + x - x^{2}} .$

Khi đó b-a bằng

A. $\frac{1}{2}$

B. 2

C. $\frac{7}{2}$

D. $\frac{5}{2}$

Xem đáp án

Câu 48:

Cho (H) là hình phẳng giới hạn bởi parabol $y = \sqrt{3} x^{2}$ và nửa đường tròn có phương trình $y = \sqrt{4 - x^{2}} với - 2 \leq x \leq 2$ (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

A. $\frac{2 π + 5 \sqrt{3}}{3} .$

B. $\frac{4 π + 5 \sqrt{3}}{3} .$

C. $\frac{4 π + \sqrt{3}}{3} .$

D. $\frac{2 π + \sqrt{3}}{3} .$

Xem đáp án

Câu 49:

Cho số phức z thỏa mãn điều kiện $|z + 2| = |z + 2 i| .$ Giá trị nhỏ nhất của biểu thức $P = |z - 1 - 2 i| + |z - 3 - 4 i| + |z - 5 - 6 i|$ được viết dưới dạng $(a + b \sqrt{17}) / \sqrt{2}$ với a,b là các hữu tỉ. Giá trị của a+b là

A. 3

B. 2

C. 7

D. 4

Xem đáp án

Câu 50:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của BC và H là trung điểm của AM. Biết $H B = H C, \hat{H B C} = 30^{0};$ góc giữa mặt phẳng (SHC) và mặt phẳng (HBC) bằng $60^{0} .$ Tính cô-sin của góc giữa đường thẳng BC và mặt phẳng (SHC).

A. $\frac{1}{2}$

B. $\frac{\sqrt{3}}{2}$

C. $\frac{\sqrt{13}}{4}$

D. $\frac{\sqrt{3}}{4}$

Xem đáp án

Bắt đầu thi ngay

Bài thi liên quan

Đề số 1
- 33 câu hỏi
- 90 phút
Đề số 2
- 53 câu hỏi
- 90 phút
Đề số 3
- 50 câu hỏi
- 90 phút
Đề số 4
- 50 câu hỏi
- 90 phút
Đề số 5
- 50 câu hỏi
- 90 phút
Đề số 6
- 50 câu hỏi
- 90 phút
Đề số 7
- 50 câu hỏi
- 90 phút
Đề số 8
- 50 câu hỏi
- 90 phút
Đề số 9
- 50 câu hỏi
- 90 phút
Đề số 10
- 50 câu hỏi
- 90 phút

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)

Đề số 26

Danh sách câu hỏi

Bài thi liên quan