Giải VTH Toán 7 KNTT Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án
Giải VTH Toán 7 KNTT Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án
-
321 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong tam giác ABC, các đường trung tuyến AM, BN, CP đồng quy tại điểm G. Khi đó ta có:
A. \(\frac{{GA}}{{MA}} = \frac{1}{2}\);
B. \(\frac{{GB}}{{NG}} = \frac{1}{2}\);
C. \(\frac{{GC}}{{PC}} = \frac{2}{3}\);
D. \(\frac{{MA}}{{GA}} = \frac{2}{3}\).
Xem đáp án
Đáp án đúng là: C
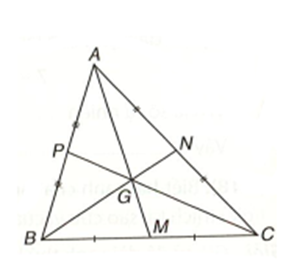
Trong tam giác ABC, các đường trung tuyến AM, BN, CP đồng quy tại điểm G nên G là trọng tâm của tam giác.
Khi đó ta có: \(\frac{{GA}}{{MA}} = \frac{{GB}}{{NB}} = \frac{{GC}}{{PC}} = \frac{2}{3}\). Vậy trong các đáp án đã cho chỉ có đáp án C đúng.
Câu 2:
Với giả thiết như ở Câu 1, phương án nào sau đây là sai?
A. GA = 2GM;
B. \(\frac{{NG}}{{GB}} = \frac{1}{2}\);
C. \(\frac{{PG}}{{PC}} = \frac{1}{3}\);
D. \(\frac{{MA}}{{GA}} = \frac{2}{3}\).
Xem đáp án
Đáp án đúng là: D
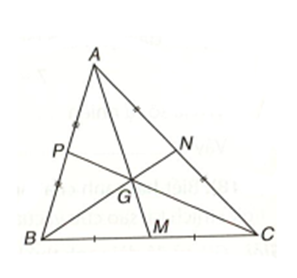
Theo Câu 1, ta có: \(\frac{{GA}}{{MA}} = \frac{{GB}}{{NB}} = \frac{{GC}}{{PC}} = \frac{2}{3}\).
Từ \(\frac{{GA}}{{MA}} = \frac{2}{3}\), suy ra 3GA = 2MA hay 3GA = 2(GA + GM). Suy ra GA = 2GM. Vậy đáp án A đúng.
Tương tự, ta có GB = 2NG, suy ra \(\frac{{NG}}{{GB}} = \frac{1}{2}\). Vậy đáp án B đúng.
Từ \(\frac{{GC}}{{PC}} = \frac{2}{3}\), suy ra 3GC = 2PC hay 3(PC – PG) = 2PC, suy ra PC = 3PG.
Do đó, \(\frac{{PG}}{{PC}} = \frac{1}{3}\). Vậy đáp án C đúng.
Đáp án D sai do \(\frac{{GA}}{{MA}} = \frac{2}{3}\), suy ra \(\frac{{MA}}{{GA}} = \frac{3}{2}\).
Câu 3:
Cho tam giác ABC có các đường phân giác AD, BE, CF. Hãy điền vào chỗ trống để được khẳng định đúng.
Nếu AD, BE cắt nhau tại I thì CF ....................... I.
Xem đáp án
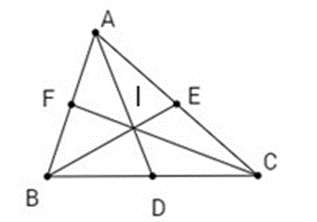
Nếu AD, BE cắt nhau tại I thì CF đi qua I.
Câu 4:
Cho tam giác ABC có các đường phân giác AD, BE, CF. Hãy điền vào chỗ trống để được khẳng định đúng.
Nếu I là điểm chung của ba đường phân giác thì I ......................................................
Xem đáp án
Nếu I là điểm chung của ba đường phân giác thì I là giao điểm của ba đường phân giác này và cách đều ba cạnh của tam giác ABC.
Câu 5:
Gọi I là giao điểm của ba đường phân giác của tam giác. Kết luận nào sau đây là đúng?
A. I không cách đều ba cạnh của tam giác;
B. I cách đều ba đỉnh của tam giác;
C. I là trọng tâm của tam giác;
D. I cách đều ba cạnh của tam giác.
Xem đáp án
Đáp án đúng là: D
I là giao điểm của ba đường phân giác của tam giác nên I cách đều ba cạnh của tam giác.
Câu 6:
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu “?” để được các đẳng thức:
BG = ? BN, CG = ? CP; BG = ? GN, CG = ? GP.
Xem đáp án
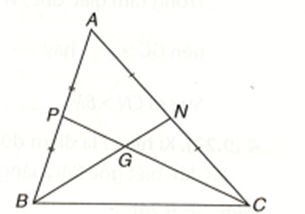
Vì G là trọng tâm của tam giác ABC nên ta có:
BG = \[\frac{2}{3}\]BN, CG = \[\frac{2}{3}\]CP,
BG = 2 GN, CG = 2 GP.
Câu 7:
Chứng minh rằng:
Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.
Xem đáp án
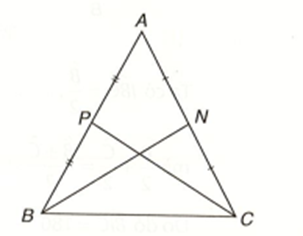
Tam giác ABC cân tại A và có BN, CP là hai đường trung tuyến. Ta cần chứng minh BN = CP.
Tam giác ABC cân tại A nên AB = AC; \[\widehat {PBC} = \widehat {NCB}\].
Do N, P lần lượt là trung điểm của AC, AB nên BP = \(\frac{1}{2}\)AB, CN = \(\frac{1}{2}\)AC, do đó BP = CN.
Xét hai tam giác BCP và CBN, ta có:
BP = CN; \[\widehat {PBC} = \widehat {NCB}\]; BC chung, do đó ∆BCP = ∆CBN (c.g.c).
Suy ra CP = BN.
Câu 8:
Chứng minh rằng:
Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Xem đáp án
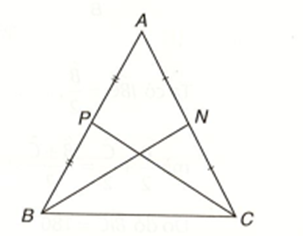
BN, CP là hai đường trung tuyến của tam giác ABC, BN = CP. Ta sẽ chứng minh AB = AC.
Gọi G là trọng tâm của tam giác ABC.
Xét hai tam giác PGB và NGC, ta có:
PG = NG; BG = CG; \(\widehat {BGP} = \widehat {CGN}\) (đối đỉnh).
Vậy ∆PGB = ∆NGC (c.g.c), suy ra BP = NC.
Do đó AB = 2PB = 2NC = AC.
Vậy tam giác ABC cân tại A.
Câu 9:
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Xem đáp án
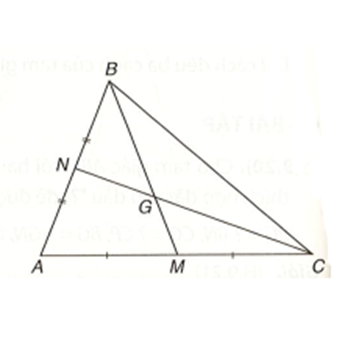
Trong tam giác GBC, vì \[\widehat {GBC} > \widehat {GCB}\] nên GC > GB hay \[\frac{2}{3}\]CN > \[\frac{2}{3}\]BM.
Suy ra CN > BM.
Câu 10:
Xem đáp án
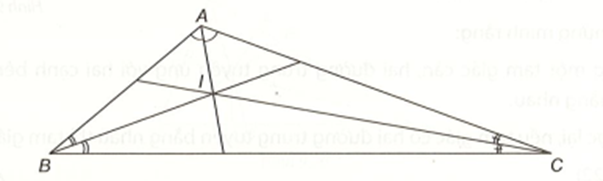
Ta có \(\widehat {IBC} = \frac{{\widehat B}}{2},\,\,\widehat {ICB} = \frac{{\widehat C}}{2}\), \[\widehat {BIC} = 180^\circ - \left( {\frac{{\widehat B}}{2} + \frac{{\widehat C}}{2}} \right)\],
mà \(\frac{{\widehat B}}{2} + \frac{{\widehat C}}{2} = \frac{{\widehat B + \widehat C}}{2} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \).
Do đó \[\widehat {BIC}\] = 180° – 30° = 150°.
Câu 11:
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
Xem đáp án
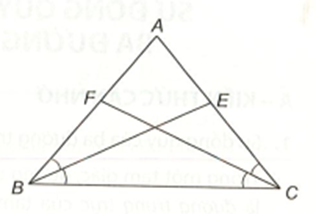
Do ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].
Do BE là tia phân giác của \[\widehat {ABC}\] nên \[\widehat {ABC} = 2\widehat {EBC}\].
Do CF là tia phân giác của \[\widehat {ACB}\] nên \[\widehat {ACB} = 2\widehat {FCB}\].
Mà \[\widehat {ABC} = \widehat {ACB}\] nên \[\widehat {EBC} = \widehat {FCB}\].
Xét ∆FBC và ∆ECB có:
\[\widehat {FCB} = \widehat {EBC}\] (chứng minh trên).
BC chung.
\[\widehat {FBC} = \widehat {ECB}\] (do \[\widehat {ABC} = \widehat {ACB}\]).
Suy ra ∆FBC = ∆ECB (g.c.g).
Do đó CF = BE (2 cạnh tương ứng).
Câu 12:
Cho tam giác ABC vuông tại A có góc B bằng 60°. Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (M ∈ BC).
Chứng minh ∆ABE = ∆MBE.
Xem đáp án
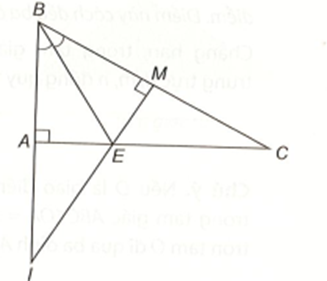
Xét hai tam giác vuông ABE và MBE, ta có:
BE cạnh chụng, \(\widehat {ABE} = \widehat {MBE}\) (BE là tia phân giác góc ABC).
Do đó ∆ABE = ∆MBE (cạnh huyền – góc nhọn).
Câu 13:
Cho tam giác ABC vuông tại A có góc B bằng 60°. Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (M ∈ BC).
Chứng minh MB = MC.
Xem đáp án
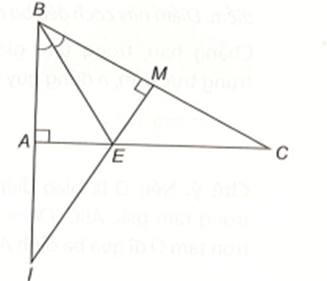
Trong tam giác vuông ABC, ta có \(\widehat B = 60^\circ \)nên \(\widehat C = 90^\circ - 60^\circ = 30^\circ \).
Vì BE là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABE} = \widehat {CBE} = \frac{{\widehat {ABC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).
Vậy tam giác BEC có \(\widehat C = \widehat {CBE} = 30^\circ \) nên tam giác BEC cân tại E.
Tam giác BEC cân tại E và có EM là đường cao nên cũng là trung tuyến , suy ra MB = MC.
Câu 14:
Cho tam giác ABC vuông tại A có góc B bằng 60°. Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (M ∈ BC).
Gọi I là giao điểm của BA và ME. Chứng minh IE > EM.
Xem đáp án
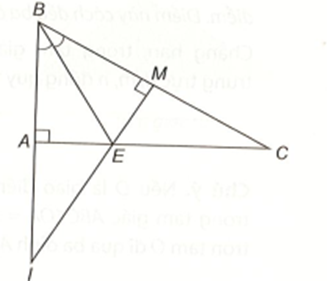
Ta có góc \(\widehat {EAI}\) kề bù với góc vuông \(\widehat {BAC}\) nên \(\widehat {EAI} = 90^\circ \).
Trong tam giác vuông AEI có cạnh IE là cạnh huyền nên IE > AE. (1)
Theo câu a) ∆ABE = ∆MBE nên AE = EM. (2)
Từ (1) và (2) suy ra IE > EM.