ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Giới hạn của dãy số
-
612 lượt thi
-
42 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Dãy số nào sau đây có giới hạn 0?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 2:
Biết \[\lim {u_n} = 3\]. Chọn mệnh đề đúng trong các mệnh đề sau.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 3:
Dãy số nào dưới đây không có giới hạn 0?
 Xem đáp án
Xem đáp án
Các dãy số có giới hạn 0 là:\[{u_n} = \frac{1}{{\sqrt n }},{u_n} = \frac{1}{{\sqrt[3]{n}}},{u_n} = 0\]
Dãy số \[\left( {{u_n}} \right)\]ở đáp án C có\[\lim {u_n} = \lim \frac{{\sqrt[3]{n}}}{2} = + \infty \]
Đáp án cần chọn là: C
Câu 4:
Cho hai dãy số \[\left( {{u_n}} \right),\left( {{v_n}} \right)\]thỏa mãn \[\left| {{u_n}} \right| \le {v_n}\] với mọi n và \[\lim {u_n} = 0\] thì:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 5:
Cho \[n \in {N^ * }\] nếu \[|q| < 1\;\]thì:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 6:
Dãy số (un) có giới hạn là số thực L nếu:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 7:
Giả sử \[\lim {u_n} = L\]. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 8:
Cho \[\lim {u_n} = L\]. Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Định lý 1: Giả sử \[\lim {u_n} = L\]Khi đó:
i) \[\lim \left| {{u_n}} \right| = \left| L \right|\]và\[\lim \sqrt[3]{{{u_n}}} = \sqrt[3]{L}\]
ii) Nếu\[{u_n} \ge 0\]với mọi n thì\[L \ge 0\]và\[\lim \sqrt {{u_n}} = \sqrt L \]
Từ định lý trên ta thấy chỉ có đáp án D đúng.
Đáp án cần chọn là: D
Câu 9:
Giả sử \[\lim {u_n} = L,\lim {v_n} = M\]. Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 10:
Giả sử \[\lim {u_n} = L,\lim {v_n} = M\] và c là một hằng số. Chọn mệnh đề sai:
 Xem đáp án
Xem đáp án
Giả sử\[\lim {u_n} = L,\lim {v_n} = M\]và c là một hằng số. Khi đó:
\[\lim \left( {{u_n} + {v_n}} \right) = L + M,\lim \left( {{u_n} - {v_n}} \right) = L - M,\lim \left( {{u_n}.{v_n}} \right) = L.M,\lim \left( {c.{u_n}} \right) = c.L\]
Đáp án cần chọn là: D
Câu 11:
Cho cấp số nhân lùi vô hạn \[\left( {{u_n}} \right)\]công bội q. Đặt \[S = {u_1} + {u_2} + ... + {u_n} + ...\] thì:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 12:
Chọn mệnh đề sai:
 Xem đáp án
Xem đáp án
Ta có:\[\lim n = + \infty ,\lim \sqrt n = + \infty ,\lim \sqrt[3]{n} = + \infty ,\lim \frac{1}{n} = 0\]
Vậy chỉ có đáp án D là sai.
Đáp án cần chọn là: D
Câu 13:
Cho các dãy số \[{u_n} = \frac{1}{n},n \ge 1\]và \({v_n} = {n^2},n \ge 1\). Khi đó:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 14:
Trong các khẳng định sau, khẳng định nào sai:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 15:
Gọi S là tổng của cấp số nhân lùi vô hạn \[\left( {{u_n}} \right)\;\]có công bội \[q\left( {\left| q \right| < 1} \right)\]. Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 16:
Cho \[{u_n} = \frac{{1 - 4n}}{{5n}}\]. Khi đó \[lim\,{u_n}\]bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 17:
Cho \[{u_n} = \frac{{{n^2} - 3n}}{{1 - 4{n^3}}}\]. Khi đó \[lim\,{u_n}\]bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 18:
Cho \[{u_n} = \frac{{{n^2} - 3n}}{{1 - 4{n^3}}}\]. Khi đó \[lim\,{u_n}\]bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 19:
Cho \[{u_n} = \frac{{{3^n} + {5^n}}}{{{5^n}}}\]. Khi đó \[lim\,{u_n}\]bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 20:
Trong các giới hạn sau giới hạn nào bằng −1?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 21:
Giá trị \[\lim \left( {{n^3} - 2n + 1} \right)\] bằng
 Xem đáp án
Xem đáp án
Ta có:\[{n^3} - 2n + 1 = {n^3}\left( {1 - \frac{2}{{{n^2}}} + \frac{1}{{{n^3}}}} \right)\]
Vì\[\lim {n^3} = + \infty \] và\[\lim \left( {1 - \frac{2}{{{n^2}}} + \frac{1}{{{n^3}}}} \right) = 1 >0\] nên\[\lim \left( {{n^3} - 2n + 1} \right) = + \infty \]
Đáp án cần chọn là: D
Câu 22:
Giới hạn \[\lim \frac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}\] bằng?
 Xem đáp án
Xem đáp án
Bước 1:
\[\lim \frac{{{2^{n + 1}} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}} = \lim \frac{{{{2.2}^n} - {{3.5}^n} + 5}}{{{{3.2}^n} + {{9.5}^n}}}\]
\[ = \lim \frac{{2.{{\left( {\frac{2}{5}} \right)}^n} - 3 + 5.{{\left( {\frac{1}{5}} \right)}^n}}}{{3.{{\left( {\frac{2}{5}} \right)}^n} + 9}}\]
Bước 2:
\[ = \frac{{2.0 - 3 + 5.0}}{{3.0 + 9}} = \frac{{ - 3}}{9} = - \frac{1}{3}.\]
Đáp án cần chọn là: D
Câu 23:
Giới hạn \[\lim \frac{{{{\left( {2 - 5n} \right)}^3}{{\left( {n + 1} \right)}^2}}}{{2 - 25{n^5}}}\] bằng?
 Xem đáp án
Xem đáp án
\[\lim \frac{{{{(2 - 5n)}^3}{{(n + 1)}^2}}}{{2 - 25{n^5}}} = \lim \frac{{\frac{{{{(2 - 5n)}^3}}}{{{n^3}}}.\frac{{{{(n + 1)}^2}}}{{{n^2}}}}}{{\frac{{2 - 25{n^5}}}{{{n^5}}}}} = \frac{{{{\left( {\frac{{2 - 5n}}{n}} \right)}^3}.{{\left( {\frac{{n + 1}}{n}} \right)}^2}}}{{\frac{2}{{{n^5}}} - 25}}\]
\[ = \lim \frac{{{{\left( {\frac{2}{n} - 5} \right)}^3}.{{\left( {1 + \frac{1}{n}} \right)}^2}}}{{\frac{2}{{{n^5}}} - 25}} = \frac{{{{\left( {0 - 5} \right)}^3}{{\left( {1 + 0} \right)}^2}}}{{0 - 25}} = \frac{{{{( - 5)}^3}{{.1}^2}}}{{ - 25}} = 5\]
Đáp án cần chọn là: C
Câu 24:
Giới hạn \[\lim \frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}\] bằng?
 Xem đáp án
Xem đáp án
Cách 1:
\[\begin{array}{l}lim\frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}\\ = lim\frac{{\left( {\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} } \right).\left( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} } \right)}}{{\left( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} } \right).\left( {2n - 1} \right)}}\\ = lim\frac{{({n^2} - 3n - 5) - (9{n^2} + 3)}}{{\left( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} } \right).\left( {2n - 1} \right)}}\\ = lim\frac{{ - 8{n^2} - 3n - 8}}{{\left( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} } \right).\left( {2n - 1} \right)}}\\ = lim\frac{{ - 8 - \frac{3}{n} - \frac{8}{{{n^2}}}}}{{\left( {\sqrt {1 - \frac{3}{n} - \frac{5}{{{n^2}}}} + \sqrt {9 + \frac{3}{{{n^2}}}} } \right)\left( {2 - \frac{1}{n}} \right)}} = \frac{{ - 8}}{{4.2}} = - 1\end{array}\]
Cách 2: Chia cả tử và mẫu cho n.
\[\lim \frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}} = \lim \frac{{\sqrt {1 - \frac{3}{n} - \frac{5}{{{n^2}}}} - \sqrt {9 + \frac{3}{{{n^2}}}} }}{{2 - \frac{1}{n}}} = \lim \frac{{1 - 3}}{2} = - 1\]
Đáp án cần chọn là: D
Câu 25:
Giới hạn \[\lim \frac{{2{n^2} - n + 4}}{{\sqrt {2{n^4} - {n^2} + 1} }}\] bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 26:
Giới hạn \[\lim \left( {\sqrt {{n^2} - n} - n} \right)\] bằng?
 Xem đáp án
Xem đáp án
\[\lim \left( {\sqrt {{n^2} - n} - n} \right) = \lim \frac{{\left( {\sqrt {{n^2} - n} - n} \right).\left( {\sqrt {{n^2} - n} + n} \right)}}{{\sqrt {{n^2} - n} + n}}\]
\[ = \lim \frac{{{n^2} - n - {n^2}}}{{\sqrt {{n^2} - n} + n}} = \lim \frac{{ - n}}{{\sqrt {{n^2} - n} + n}} = \lim \frac{{ - 1}}{{\sqrt {1 - \frac{1}{n}} + 1}} = \frac{{ - 1}}{2} = - \frac{1}{2}.\]
Đáp án cần chọn là: B
Câu 27:
Giới hạn \[\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)\] bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 28:
Cho dãy số \[\left( {{u_n}} \right)\]với \[{u_n} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + .... + \frac{1}{n} - \frac{1}{{n + 1}}\]. Khi đó \[lim\,{u_n}\] bằng?
 Xem đáp án
Xem đáp án
\[{u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{n.\left( {n + 1} \right)}}\]
\[ = \frac{{2 - 1}}{{1.2}} + \frac{{3 - 2}}{{2.3}} + ... + \frac{{n + 1 - n}}{{n.\left( {n + 1} \right)}}\]
\[ = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + .... + \frac{1}{n} - \frac{1}{{n + 1}}\]
\[ = 1 - \frac{1}{{n + 1}}\]
\[ \Rightarrow \lim {u_n} = \lim \left( {1 - \frac{1}{{n + 1}}} \right) = 1.\]
Đáp án cần chọn là: C
Câu 29:
Cho dãy số \[({u_n})\]với \[{u_n} = \frac{1}{{1.3}} + \frac{1}{{3.5}} + ... + \frac{1}{{\left( {2n - 1} \right).\left( {2n + 1} \right)}}\]
Khi đó \[lim\,{u_n}\] bằng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 30:
Giá trị \[\lim \frac{{\sin \left( {n!} \right)}}{{{n^2} + 1}}\] bằng
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 31:
Cho dãy số \[({u_n})\]với \[{u_n} = \frac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}\] Khi đó \[lim\,{u_n}\] bằng?
 Xem đáp án
Xem đáp án
\[\lim {u_n} = \lim \frac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}} = \lim \frac{{ - 6{n^2} - n + 1}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}\]
\[ = \lim \frac{{\frac{{ - 6{n^2} - n + 1}}{{{n^2}}}}}{{\sqrt[3]{{\frac{{{n^3} + 5n - 1}}{{{n^6}}}}}}} = \lim \frac{{ - 6 - \frac{1}{n} + \frac{1}{{{n^2}}}}}{{\sqrt[3]{{\frac{1}{{{n^3}}} + \frac{5}{{{n^5}}} - \frac{1}{{{n^6}}}}}}} = - \infty .\]
Đáp án cần chọn là: A
Câu 32:
Cho dãy số \[({u_n})\]xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 2}\\{{u_{n + 1}} = \frac{{{u_n} + 1}}{2},\left( {n \ge 1} \right)}\end{array}} \right.\) Khi đó mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
\[{u_2} = \frac{{2 + 1}}{2} = \frac{3}{2} = \frac{{{2^1} + 1}}{{{2^1}}}\]
\[{u_3} = \frac{{\frac{3}{2} + 1}}{2} = \frac{5}{4} = \frac{{{2^2} + 1}}{{{2^2}}}\]
\[{u_4} = \frac{{\frac{5}{4} + 1}}{2} = \frac{9}{8} = \frac{{{2^3} + 1}}{{{2^3}}}\]
Chứng minh bằng quy nạp:\[{u_{n + 1}} = \frac{{{2^n} + 1}}{{{2^n}}},\,\,\forall n = 1;2;...\,\,\,\,( * )\]
* Với\[n = 1:{u_2} = \frac{{{u_1} + 1}}{2} = \frac{{2 + 1}}{2} = \frac{{{2^1} + 1}}{{{2^1}}}\]: (*) đúng
* Giả sử (*) đúng với\[n = k \ge 1\] tức là\[{u_k} = \frac{{{2^k} + 1}}{{{2^k}}}\] ta chứng minh (*) đúng với\[n = k + 1\]tức là cần chứng minh\[{u_{k + 1}} = \frac{{{2^{k + 1}} + 1}}{{{2^{k + 1}}}}\]
Ta có :
\[{u_{k + 1}} = \frac{{{u_k} + 1}}{2} = \frac{{\frac{{{2^k} + 1}}{{{2^k}}} + 1}}{2} = \frac{{\frac{{{2^k} + 1 + {2^k}}}{{{2^k}}}}}{2} = \frac{{{{2.2}^k} + 1}}{{{2^{k + 1}}}} = \frac{{{2^{k + 1}} + 1}}{{{2^{k + 1}}}}\]
Theo nguyên lý quy nạp, ta chứng minh được (*).
Như vậy, công thức tổng quát của dãy \[({u_n})\]là:
\[{u_n} = \frac{{{2^{n - 1}} + 1}}{{{2^{n - 1}}}} = 1 + \frac{1}{{{2^{n - 1}}}},\,\,\forall n = 1;2;...\,\,\,\,( * )\]
Từ (*) ta có\[{u_{n + 1}} - {u_n} = 1 + \frac{1}{{{2^n}}} - \left( {1 + \frac{1}{{{2^{n - 1}}}}} \right)\]
\[ = \frac{1}{{{2^n}}} - \frac{1}{{{2^{n + 1}}}} < 0\,\,\forall n = 1,2,... \Rightarrow \left( {{u_n}} \right)\]là dãy giảm và
\[\lim {u_n} = \lim \left( {1 + \frac{1}{{{2^{n - 1}}}}} \right) = 1 \Rightarrow \]là dãy giảm tới 1 khi\[n \to + \infty \]
Đáp án cần chọn là: A
Câu 33:
Cho các số thực a, b thỏa \[\left| a \right| < 1,\;\;\left| b \right| < 1\]. Tìm giới hạn \[I = lim\frac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}\].
 Xem đáp án
Xem đáp án
Ta có\[1,\;a,\;{a^2},\;...,\;{a^n}\] là một cấp số nhân có công bội a
\[ \Rightarrow 1 + a + {a^2} + ... + {a^n} = \frac{{1 - {a^{n + 1}}}}{{1 - a}}.\]
Tương tự: \[1 + b + {b^2} + ... + {b^n} = \frac{{1 - {b^{n + 1}}}}{{1 - b}}\]
\[ \Rightarrow \lim I = \lim \frac{{\frac{{1 - {a^{n + 1}}}}{{1 - a}}}}{{\frac{{1 - {b^{n + 1}}}}{{1 - b}}}} = \lim \left( {\frac{{1 - {a^{n + 1}}}}{{1 - a}}.\frac{{1 - b}}{{1 - {b^{n + 1}}}}} \right) = \lim \left( {\frac{{1 - {a^{n + 1}}}}{{1 - {b^{n + 1}}}}.\frac{{1 - b}}{{1 - a}}} \right) = \frac{{1 - b}}{{1 - a}}.\]
(Vì\[\left| a \right| < 1,\;\;\left| b \right| < 1 \Rightarrow \lim {a^{n + 1}} = \lim {b^{n + 1}} = 0\])
Đáp án cần chọn là: C
Câu 34:
Cho dãy số \[\left( {{u_n}} \right)\]xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_{n + 1}} = \sqrt {{u_n}({u_n} + 1)({u_n} + 2)({u_n} + 3) + 1} }\end{array}} \right.\left( {n \ge 1} \right)\) Đặt \[{v_n} = \sum\limits_{i = 1}^n {\frac{1}{{{u_i} + 2}}} \]. Tính \[lim\,{v_n}\]bằng?
 Xem đáp án
Xem đáp án
\[{u_2} = \sqrt {1.2.3.4 + 1} = 5,{u_n} >0,\forall n = 1;2;...\]
Ta có:
\[{u_{n + 1}} = \sqrt {{u_n}({u_n} + 1)({u_n} + 2)({u_n} + 3) + 1} \]
\[ = \sqrt {(u_n^2 + 3{u_n})(u_n^2 + 3{u_n} + 2) + 1} \]
\[ = \sqrt {{{(u_n^2 + 3{u_n})}^2} + 2(u_n^2 + 3{u_n}) + 1} \]
\[ = \sqrt {{{(u_n^2 + 3{u_n} + 1)}^2}} = u_n^2 + 3{u_n} + 1\]
\(\begin{array}{l} \Rightarrow {u_{n + 1}} + 1 = u_n^2 + 3{u_n} + 2 = ({u_n} + 1)({u_n} + 2)\\ \Rightarrow \frac{1}{{{u_{n + 1}} + 1}} = \frac{1}{{({u_n} + 1)({u_n} + 2)}} = \frac{1}{{{u_n} + 1}} - \frac{1}{{{u_n} + 2}}\\ \Rightarrow \frac{1}{{{u_n} + 2}} = \frac{1}{{{u_n} + 1}} - \frac{1}{{{u_{n + 1}} + 1}}\end{array}\)
Do đó:
\(\begin{array}{l}\\{v_n} = \mathop \sum \limits_{i = 1}^n \frac{1}{{{u_i} + 2}} = \mathop \sum \limits_{i = 1}^n \left( {\frac{1}{{{u_i} + 1}} - \frac{1}{{{u_{i + 1}} + 1}}} \right)\end{array}\)
\[ = \frac{1}{{{u_1} + 1}} - \frac{1}{{{u_{n + 1}} + 1}} = \frac{1}{2} - \frac{1}{{{u_{n + 1}} + 1}}\]
Xét hiệu\[{u_{n + 1}} - {u_n} = u_n^2 + 3{u_n} + 1 - {u_n} = {\left( {{u_n} + 1} \right)^2} >0\]
\[ \Rightarrow \left( {{u_n}} \right)\]là dãy tăng.
Giả sử
\[\lim {u_{n + 1}} = \lim {u_n} = a >0 \Rightarrow a = {a^2} + 3a + 1 \Rightarrow {a^2} + 2a + 1 = 0 \Leftrightarrow a = - 1\,\,\left( {ktm} \right) \Rightarrow \lim {u_n} = + \infty \]\[ \Rightarrow \lim {v_n} = \frac{1}{2} - \frac{1}{{{u_{n + 1}} + 1}} = \frac{1}{2} - 0 = \frac{1}{2}.\]
Đáp án cần chọn là: C
Câu 35:
Giá trị của \[B = {\rm{lim}}\frac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }}\] bằng:
 Xem đáp án
Xem đáp án
Ta có:\[n! < {n^n} \Rightarrow \sqrt[n]{{n!}} < \sqrt[n]{{{n^n}}}\]
\[ \Rightarrow 0 < \frac{{\sqrt[{\rm{n}}]{{n!}}}}{{\sqrt {{n^3} + 2n} }} < \frac{{\sqrt[{\rm{n}}]{{{n^n}}}}}{{\sqrt {{n^3} + 2n} }} = \frac{n}{{\sqrt {{n^3} + 2n} }}\]
Mà\[\lim 0 = 0\,;\;\,\,\lim \,\frac{n}{{\sqrt {{n^3} + 2n} }} = \lim \frac{n}{{n\sqrt {n + \frac{2}{n}} }} = \lim \frac{1}{{\sqrt {n + \frac{2}{n}} }} = 0\]
\[ \Rightarrow \lim \frac{{\sqrt[n]{{n!}}}}{{\sqrt {{n^3} + 2n} }} = 0 \Rightarrow B = 0.\]
Đáp án cần chọn là: C
Câu 36:
\[\lim \left( {\frac{2}{n} + \frac{3}{{{n^2}}}} \right)\]bằng
 Xem đáp án
Xem đáp án
Bước 1:
Vì \[\lim \frac{1}{n} = 0;\lim \frac{1}{{{n^2}}} = 0\]
Bước 2:
Nên\[\lim \left( {\frac{2}{n} + \frac{3}{{{n^2}}}} \right) = 2.0 + 3.0 = 0\]
Đáp án cần chọn là: B
Câu 37:
Tính giới hạn \[\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}}\].
 Xem đáp án
Xem đáp án
Bước 1:
\[\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}} = \lim \frac{{{n^3}\left( { - 3 + \frac{1}{n}} \right)}}{{{n^3}\left( {2 + \frac{5}{n} - \frac{2}{{{n^3}}}} \right)}}\]
Bước 2:
\[ = \lim \frac{{ - 3 + \frac{1}{n}}}{{2 + \frac{5}{n} - \frac{2}{{{n^3}}}}} = \frac{{ - 3 + 0}}{{2 + 0 - 0}} = \frac{{ - 3}}{2}\]
Đáp án cần chọn là: D
Câu 38:
\[\lim \frac{{n + 1}}{{2n - 3}}\]bằng
 Xem đáp án
Xem đáp án
Bước 1:
\[\lim \frac{{n + 1}}{{2n - 3}} = \lim \frac{{n\left( {1 + \frac{1}{n}} \right)}}{{n\left( {2 - \frac{3}{n}} \right)}} = \lim \frac{{1 + \frac{1}{n}}}{{2 - \frac{3}{n}}}\]
Bước 2:
\[ = \frac{{1 + 0}}{{2 - 0}} = \frac{1}{2}\]
Đáp án cần chọn là: C
Câu 39:
Cho tam giác đều ABC cạnh a. Tam giác \[{A_1}{B_1}{C_1}\] có đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \[{A_2}{B_2}{C_2}\] có các đỉnh là trung điểm các cạnh của tam giác \[{A_1}{B_1}{C_1}\],…, tam giác AnBnCnAnBnCn có các đỉnh là trung điểm các cạnh của tam giác \[{A_{n - 1}}{B_{n - 1}}{C_{n - 1}} \ldots .{\rm{ }}Goi\;P,{P_1},{P_2},...,{P_n},...\] là chu vi của các tam giác \[ABC,{A_1}{B_1}{C_1},{A_2}{B_2}{C_2},...,{A_n}{B_n}{C_n},...\] Tìm tổng \[P,{P_1},{P_2},...,{P_n},...\]
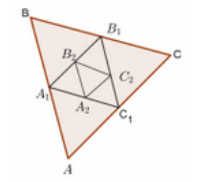
 Xem đáp án
Xem đáp án
Bước 1:
Gọi \[{a_n}\] là cạnh của tam giác \[{A_n}{B_n}{C_n}\] với n nguyên dương.
Ta cần chứng minh cạnh của tam giác bất kì \[{A_n}{B_n}{C_n}\] bằng\[{a_n} = \frac{a}{{{2^n}}}\] ới mọi số nguyên dương n (*)
Vì\[{A_1},{B_1},{C_1}\] là trung điểm các cạnh của tam giác ABC nên \[{a_1} = \frac{a}{2}\]
Cạnh của tam giác\[{A_1}{B_1}{C_1}\] có cạnh là\[\frac{a}{2} = \frac{a}{{{2^1}}}\]
Giả sử (*) đúng với \[n = k\]
Tức là cạnh của tam giác\[{A_k}{B_k}{C_k}\] là\[{a_k} = \frac{a}{{{2^k}}}\]
Ta có\[{A_{k + 1}}{B_{k + 1}}{C_{k + 1}}\] có cạnh bằng một nửa cạnh của tam giác\[{A_k}{B_k}{C_k}\] nên có cạnh là\[{a_{k + 1}} = \frac{{{a_k}}}{2} = \frac{1}{2}.\frac{a}{{{2^k}}} = \frac{a}{{{2^{k + 1}}}}\]
=>(*) đúng với \[n = k + 1\]
=>(*) đúng với mọi số nguyên dương n.
=>Chu vi của tam giác\[{A_n}{B_n}{C_n}\] như giả thiết là\[{P_n} = \frac{{3a}}{{{2^n}}}\]
Bước 2:
Như vậy\[P = 3a;{P_1} = \frac{{3a}}{2};{P_2} = \frac{{3a}}{{{2^2}}};...;{P_n} = \frac{{3a}}{{{2^n}}};...\]
Dãy số\[\left( {{P_n}} \right)\] gồm\[P,{P_1},{P_2},...\] là cấp số nhân với số hạng đầu là\[P = 3a\] công bội\[q = \frac{1}{2}\]
\[ \Rightarrow P + {P_1} + {P_2} + ... = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\]
Đáp án cần chọn là: B
Câu 40:
Dãy \[\left( {{u_n}} \right)\]có giới hạn \[ - \infty \] ta viết là:
 Xem đáp án
Xem đáp án
Dãy số \[\left( {{u_n}} \right)\]có giới hạn \[ - \infty \] nếu mọi số hạng của dãy số đều nhỏ hơn một số âm tùy ý cho trước kể từ một số hạng nào đó trở đi.
Khi đó, ta viết\[\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}} \right) = - \infty \]viết tắt là\[\lim \left( {{u_n}} \right) = - \infty \] hoặc\[\lim {u_n} = - \infty \]
Đáp án cần chọn là: B
Câu 41:
Cho cấp số nhân \[{u_n} = \frac{1}{{{2^n}}},\forall n \ge 1\]. Khi đó:
 Xem đáp án
Xem đáp án
Ta có:\[{u_1} = \frac{1}{2};q = \frac{1}{2} \Rightarrow S = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{1}{2}}}{{1 - \frac{1}{2}}} = 1\]
Đáp án cần chọn là: A
Câu 42:
![Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có cạnh bằng a và có diện tích \[{S_1}\]. Nối bốn trung điểm \[{A_2},{B_2},{C_2},{D_2}\;\] ta được hình vuông thứ hai có diện tích \[{S_2}\]. Tiếp tục (ảnh 1)](https://video.vietjack.com/upload2/images/1653298186/1653298389-image2.png)
Cho hình vuông \[{A_1}{B_1}{C_1}{D_1}\] có cạnh bằng a và có diện tích \[{S_1}\]. Nối bốn trung điểm \[{A_2},{B_2},{C_2},{D_2}\;\] ta được hình vuông thứ hai có diện tích \[{S_2}\]. Tiếp tục như thế, ta được hình vuông \[{A_3}{B_3}{C_3}{D_3}\] có diện tích \[{S_3}, \ldots \;\] Tính tổng \[{S_1} + {S_2} + \ldots \;\] bằng
 Xem đáp án
Xem đáp án
Bước 1: Tìm cấp số nhân
Ta có:
\[\begin{array}{l}{{\rm{S}}_1} = {a^2}\\{{\rm{S}}_2} = {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = {a^2} \cdot \frac{1}{2}\\{{\rm{S}}_3} = {\left( {\frac{{a\sqrt 2 }}{2} \cdot \frac{{\sqrt 2 }}{2}} \right)^2}\\ \cdots \\{{\rm{S}}_{\rm{n}}} = {a^2} \cdot {\left( {\frac{1}{2}} \right)^{n - 1}}\end{array}\]
Có\[{S_1};{S_2};{S_3}; \ldots \] là một cấp số nhân lùi vô hạn với:
- Số hạng đầu:\[{S_1} = {a^2}\]
- Công bội:\[q = \frac{1}{2}\]
Bước 2: Sử dụng công thức tổng cấp số nhân lùi vô hạn
Do đó:\[S = {S_1} + {S_2} + {S_3} + \ldots = \frac{{{S_1}}}{{1 - q}} = \frac{{{a^2}}}{{1 - \frac{1}{2}}} = 2{a^2}\]
Đáp án cần chọn là: B
