Đáp án cần chọn là: C

Đáp án cần chọn là: D

Ta có

$\left\{ {\begin{array}{*{20}{c}}{{d_1}:3x + 4y + 12 = 0 \to \overrightarrow {{n_1}} = (3;4)}\\{{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 + at}\\{y = 1 - 2t}\end{array} \to \overrightarrow {{n_2}} = (2;a)} \right.}\end{array}} \right.$

$\varphi = \left( {{d_1};{d_2}} \right) = {45^0} \Rightarrow \frac{1}{{\sqrt 2 }} = \cos {45^0} = \cos \varphi = \frac{{\left| {6 + 4a} \right|}}{{\sqrt {25} .\sqrt {{a^2} + 4} }}$

$\begin{array}{l} \Leftrightarrow 25({a^2} + 4) = 8(4{a^2} + 12a + 9) \Leftrightarrow 7{a^2} + 96a - 28 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a = - 14}\\{a = \frac{2}{7}}\end{array}} \right.\end{array}$

Đáp án cần chọn là: A

Đáp án cần chọn là: C

Đáp án cần chọn là: C

Đáp án cần chọn là: A

Đáp án cần chọn là: B

$d\left( {A;{\rm{\Delta }}} \right) = \frac{{\left| { - m + 2 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5 \Leftrightarrow \left| {m - 3} \right| = \sqrt 5 .\sqrt {{m^2} + 1}$

$\Leftrightarrow 4{m^2} + 6m - 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = - 2}\\{m = \frac{1}{2}}\end{array}} \right.$

Đáp án cần chọn là: B

+) TH1: (d) không có hệ số góc.

Khi đó phương trình (d) có dạng: x – c = 0.

(d) đi qua M(1;2) nên x – 1 = 0 nên có VTPT$\vec n = \left( {1;0} \right)$

$\Rightarrow \cos \left( {d,{\rm{\Delta }}} \right) = \frac{{\left| {\overrightarrow {{n_{\rm{\Delta }}}} .\overrightarrow {{n_d}} } \right|}}{{\left| {\overrightarrow {{n_{\rm{\Delta }}}} } \right|.\left| {\overrightarrow {{n_d}} } \right|}} = \frac{{\left| {3.1 - 2.0} \right|}}{{\sqrt {{3^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{1^2} + {0^2}} }} = \frac{1}{{\sqrt {13} }} \ne \frac{{\sqrt 2 }}{2} = \cos {45^0}$

Do đó đường thẳng này không thỏa mãn bài toán.

+) TH2: (d) có hệ số góc.

PTĐT (d)được viết dưới dạng:$y - 2 = k\left( {x - 1} \right) \Leftrightarrow kx - y + 2 - k = 0$

Vì (d) hợp với $(\Delta )\;$một góc ${45^0}$ nên:${\rm{cos}}{45^0} = \frac{{|3k + ( - 1).( - 2)|}}{{\sqrt {{k^2} + 1} .\sqrt {{3^2} + {{( - 2)}^2}} }}$

$\Leftrightarrow \frac{{\sqrt 2 }}{2} = \frac{{|3k + 2|}}{{\sqrt {13} .\sqrt {{k^2} + 1} }} \Leftrightarrow \frac{2}{4} = \frac{{9{k^2} + 12k + 4}}{{13.({k^2} + 1)}}$

$\Leftrightarrow 5{k^2} + 24k - 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{k = \frac{1}{5}}\\{k = - 5}\end{array}} \right.$

Vậy phương trình (d) là: $\frac{1}{5}x - y + 2 - \frac{1}{5} = 0 \Leftrightarrow x - 5y + 9 = 0$ hay

$- 5x - y + 2 - ( - 5) = 0 \Leftrightarrow 5x + y - 7 = 0$

Đáp án cần chọn là: B

+) TH1: $(\Delta )\;$ không có hệ số góc, khi đó phương trình $(\Delta )\;$có dạng x = c  hay x – c = 0 .

$(\Delta )\;$đi qua điểm M(2;7) nên $2 - c = 0 \Leftrightarrow c = 2 \Rightarrow \left( {\rm{\Delta }} \right):x - 2 = 0$

Khi đó$d\left( {N,\left( {\rm{\Delta }} \right)} \right) = \frac{{\left| {1 - 2} \right|}}{{\sqrt {{1^2} + {0^2}} }} = 1$ (thỏa mãn).

Do đó ta có đường thẳng $\left( {{{\rm{\Delta }}_1}} \right):x - 2 = 0$+) TH2: $\left( {\rm{\Delta }} \right)$ có hệ số góc.

PTĐT $\left( {\rm{\Delta }} \right)$đi qua điểm M(2;7)  và có hệ số góc k  có dạng là:

$y - 7 = k\left( {x - 2} \right) \Leftrightarrow kx - y + 7 - 2k = 0$

Vì $\left( {\rm{\Delta }} \right)$cách N(1;2) một khoảng bằng 1  nên:

Ta có$d(N,\Delta ) = 1$

$\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{|k.1 - 2 + 7 - 2.k|}}{{\sqrt {{k^2} + 1} }} = 1 \Leftrightarrow \frac{{| - k + 5|}}{{\sqrt {{k^2} + 1} }} = 1 \Leftrightarrow {{( - k + 5)}^2} = {{(\sqrt {{k^2} + 1} )}^2}}\\{ \Leftrightarrow {k^2} - 10k + 25 = {k^2} + 1 \Leftrightarrow k = \frac{{12}}{5}}\end{array}$

Do đó ta có phương trình $\left( {{{\rm{\Delta }}_2}} \right)$là:$\frac{{12}}{5}x - y + 7 - 2.\frac{{12}}{5} = 0 \Leftrightarrow 12x - 5y + 11 = 0$

Vậy có hai đường thẳng cần tìm là $\left( {{{\rm{\Delta }}_1}} \right):x - 2 = 0$và$\left( {{{\rm{\Delta }}_2}} \right):12x - 5y + 11 = 0$

Đáp án cần chọn là: C

Điểm $M \in d\;$ nên tọa độ của M  phải thỏa mãn phương trình của d.

Gọi $M(2 + 2t;3 + t) \in d$

Ta có$\overrightarrow {AM} = (2 + 2t;2 + t)$

Theo giả thiết:$\overrightarrow {\left| {AM} \right|} = 5 \Leftrightarrow \sqrt {{{(2 + 2t)}^2} + {{(2 + t)}^2}} = 5$

$\Leftrightarrow {(2 + 2t)^2} + {(2 + t)^2} = 25$$\Leftrightarrow 5{t^2} + 12t - 17 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = \frac{{ - 17}}{5}}\end{array}} \right.$

Vậy có 2  điểm M  thỏa ycbt M1(4;4) và${M_2}(\frac{{ - 24}}{5};\frac{{ - 2}}{5})$

Đáp án cần chọn là: D

Vì:$\frac{1}{3} \ne \frac{3}{1}$ nên d  cắt d′

 Phương trình hai đường phân giác của các góc tạo bởi d và d′ là:

$\frac{{x + 3y - 6}}{{\sqrt {10} }} = \pm \frac{{3x + y + 2}}{{\sqrt {10} }} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + 3y - 6 = 3x + y + 2}\\{x + 3y - 6 = - (3x + y + 2)}\end{array}} \right.$

$\left\{ {\begin{array}{*{20}{c}}{x - y + 4 = 0}\\{x + y - 1 = 0}\end{array}} \right.$

Đáp án cần chọn là: B

+ Cạnh AB đi qua hai điểm A,B nên phương trình cạnh AB:$x - 2y - 2 = 0$+ Cạnh AC đi qua hai điểm A,C nên phương trình cạnh $AC:2x + y - 4 = 0$+ Phương trình hai đường phân giác của góc A:

$\frac{{x - 2y - 2}}{{\sqrt 5 }} = \pm \frac{{2x + y - 4}}{{\sqrt 5 }} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 3y - 2 = 0(d)}\\{3x - y - 6 = 0(d\prime )}\end{array}} \right.$

+ Xét đường phân giác $\left( d \right):x + 3y - 2 = 0$

Thế tọa độ điểm B  vào vế trái của$d:{t_1} = 4 + 3.1 - 2 = 5 >0$

Thế tạo độ điểm C  vào vế trái của d: ${t_2} = 1 + 3.2 - 2 = 5 >0$

Vì${t_1}.{t_2} >0$ nên B  và C  nằm cùng phía đối với d⇒d là đường phân giác ngoài

Vậy đường phân giác trong của góc A  là: $d':3x - y - 6 = 0$

Đáp án cần chọn là: A

Giả sử đường thẳng AB  qua M và có VTPT là $\vec n = \left( {a;b} \right)\,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)$

 =>VTPT của BC là:${\vec n_1} = \left( { - b;a} \right)$

 Phương trình AB có dạng: $a\left( {x - 2} \right) + b\left( {y - 1} \right) = 0 \Leftrightarrow ax + by - 2a - b = 0$BC có dạng:$- b\left( {x - 4} \right) + a\left( {y + 2} \right) = 0\; \Leftrightarrow - bx + ay + 4b + 2a = 0$

Do ABCD là hình vuông nên$d\left( {P,AB} \right) = d\left( {Q,BC} \right)$

$\Leftrightarrow \frac{{\left| { - b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{|3b + 4a|}}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{b = - 2a}\\{b = - a}\end{array}} \right.$

TH1: $b = - 2a$

Chọn$a = 1 \Rightarrow b = - 2$  ta được$AB:x - 2y - 2.1 - \left( { - 2} \right) = 0$ hay$x - 2y = 0$$BC: - \left( { - 2} \right)x + y + 4.\left( { - 2} \right) + 2.1 = 0$ hay$2x + y - 6 = 0$

CD đi qua P(2;0) và song song AB nên nhận$\overrightarrow {{n_{AB}}} = \left( {1; - 2} \right)$l àm VTPT

Do đó CD: 1(x-2) – 2(y-0) = 0 hay x-2y-2=0

AD đi qua Q(1;2) và song song BC nên nhận$\overrightarrow {{n_{BC}}} = \left( {2;1} \right)$ làm VTPT

Do đó AD: 2(x-1) + 1(y-2) = 0 hay 2x+y-4=0

TH2:$b = - a$

Chọn$a = 1 \Rightarrow b = - 1$ ta được$AB:x - y - 2.1 - \left( { - 1} \right) = 0$ hay$x - y - 1 = 0$

$BC: - \left( { - 1} \right)x + y + 4.\left( { - 1} \right) + 2.1 = 0$ hay$x + y - 2 = 0$

CD đi qua P(2;0) và song song AB nên nhận$\overrightarrow {{n_{AB}}} = \left( {1; - 1} \right)$  làm VTPT

Do đó CD: 1(x-2) – 1(y-0) = 0 hay x-y-2=0

AD đi qua Q(1;2) và song song BC nên nhận$\overrightarrow {{n_{BC}}} = \left( {1;1} \right)$ làm VTPT

Do đó AD: 1(x-1) + 1(y-2) = 0 hay x+y-3=0.

Đáp án cần chọn là: B

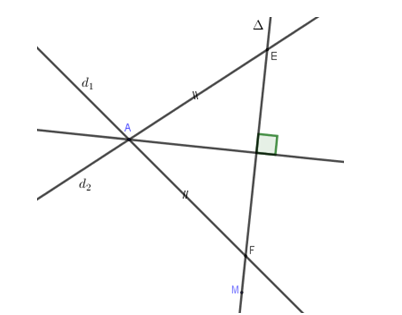
Phương trình đường phân giác góc tạo bởi ${d_1},{d_2}$ là:

$\frac{{|x - 7y + 17|}}{{\sqrt {{1^2} + {{( - 7)}^2}} }} = \frac{{|x + y - 5|}}{{\sqrt {{1^2} + {1^2}} }} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x + 6y - 21 = 0({\Delta _1})}\\{3x - y - 4 = 0({\Delta _2})}\end{array}} \right.$

Đường thẳng cần tìm đi qua M(0;1) và vuông góc  với ${{\rm{\Delta }}_1},{{\rm{\Delta }}_2}$

+ Gọi ${d_3}$ là đường thẳng vuông góc với ${{\rm{\Delta }}_1}$ thì ${d_3}$ có dạng: $3x - y + c = 0$

${d_3}$ đi qua điểm M(0;1) nên$3.0 - 1 + c = 0 \Leftrightarrow c = 1$  hay$3x - y + 1 = 0$

+ Gọi ${d_4}$ là đường thẳng vuông góc với ${{\rm{\Delta }}_2}$ thì ${d_4}$ có dạng:$x + 3y + c = 0$

${d_4}$ đi qua điểm M(0;1) nên $0 + 3.1 + c = 0 \Leftrightarrow c = - 3$ hay$x + 3y - 3 = 0$

KL: $x + 3y - 3 = 0$ và$3x - y + 1 = 0$

Đáp án cần chọn là: A

Đáp án cần chọn là: A

Đáp án cần chọn là: D

Điểm$C \in CD:x + y - 1 = 0 \Rightarrow C\left( {t;1 - t} \right)$

 Suy ra trung điểm M  của AC  là$M\left( {\frac{{t + 1}}{2};\frac{{3 - t}}{2}} \right)$

M  thuộc BM nên$(t + 1) + \frac{{3 - t}}{2} + 1 = 0 \Rightarrow t = - 7 \Rightarrow C\left( { - 7;8} \right)$

Từ A(1;2) kẻ $AI \bot CD\left( {I \in CD} \right)$cắt BC tại K

Suy ra $AK:\left( {x - 1} \right) - \left( {y - 2} \right) = 0 \Leftrightarrow x - y + 1 = 0$Tọa độ điểm I  thỏa hệ:$\left\{ {\begin{array}{*{20}{c}}{x + y - 1 = 0}\\{x - y + 1 = 0}\end{array}} \right. \Rightarrow I(0;1)$

 Tam giác ACK  cân tại C  nên I  là trung điểm của AK⇒K(−1;0)

Đường thẳng BC  đi qua C,K nên có phương trình:

$\frac{{x + 1}}{{ - 7 + 1}} = \frac{y}{8} \Leftrightarrow 4x + 3y + 4 = 0$

Đáp án cần chọn là: A

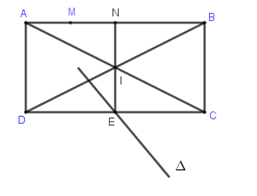
$I\left( {6;2} \right);M\left( {1;5} \right)$

${\rm{\Delta }}:x + y - 5 = 0,E \in {\rm{\Delta }} \Rightarrow E\left( {m;5 - m} \right);$

Gọi N là trung điểm của AB

I  trung điểm  NE $\Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_N} = 2{x_I} - {x_E} = 12 - m}\\{{y_N} = 2{y_I} - {y_E} = 4 - 5 + m = m - 1}\end{array}} \right.$

$\Rightarrow N\left( {12 - m;m - 1} \right)$

$\overrightarrow {MN} = \left( {11 - m;m - 6} \right);$

$\overrightarrow {IE} = \left( {m - 6;5 - m - 2} \right) = \left( {m - 6;3 - m} \right)$

$\overrightarrow {MN} .\overrightarrow {IE} = 0 \Leftrightarrow \left( {11 - m} \right)\left( {m - 6} \right) + \left( {m - 6} \right)\left( {3 - m} \right) = 0$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - 6 = 0}\\{14 - 2m = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 6}\\{m = 7}\end{array}} \right.$

$m = 6 \Rightarrow \overrightarrow {MN} = \left( {5;0} \right)$nên phương trình AB là y = 5

$m = 7 \Rightarrow \overrightarrow {MN} = \left( {4;1} \right)$ nên phương trình AB là $x - 4y + 19 = 0$Đáp án cần chọn là: A

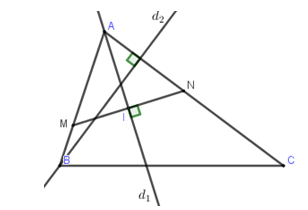
Gọi N là điểm đối xứng của M  qua ${d_1} \Rightarrow N \in AC$

$\overrightarrow {MN} = ({x_N} - 1,\,\,{y_N} + 1)$

Ta có: $\overrightarrow {MN}$cùng phương${\vec n_{{d_1}}} = (1;\,\,1)$

$\Leftrightarrow \,\,1({x_N} - 1) - 1({y_N} + 1) = 0 \Leftrightarrow {x_N} - {y_N} = 2\,\,\,(1)$

 Tọa độ trung điểm I  của$MN:{x_I} = \frac{1}{2}\left( {1 + {x_N}} \right),{y_I} = \frac{1}{2}\left( { - 1 + {y_N}} \right)$

$I \in \left( {{d_1}} \right) \Leftrightarrow \frac{1}{2}\left( {1 + {x_N}} \right) + \frac{1}{2}\left( { - 1 + {y_N}} \right) + 2 = 0 \Leftrightarrow {x_N} + {y_N} + 4 = 0\,\,\,\,(2)$

Giải hệ (1)  và (2)  ta được $N\left( { - 1; - 3} \right)$

Phương trình cạnh AC vuông góc với ${d_2}$ có dạng: $x + 2y + C = 0.$

$N \in AC \Leftrightarrow - 1 + 2.( - 3) + C = 0 \Leftrightarrow C = 7$

 Vậy, phương trình cạnh $AC:x + 2y + 7 = 0.$

Đáp án cần chọn là: CCâu 21. Xét trong mặt phẳng tọa độ Oxy, cặp điểm nào dưới đây nằm cùng phía so với đường thẳng $x - 2y + 3 = 0?$

A.M(0;1) và P(0;2).

B.P(0;2) và N(1;1).

C.M(0;1) và Q(2;−1).

D.M(0;1) và N(1;5).

Ta thế tọa độ M(0;1) và P(0;2) vào đường thẳng:

$\left( {0 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0$ nên loại A.

Ta thế tọa độ N(1;1) và P(0;2) vào đường thẳng:

$\left( {1 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0$ nên loại B.

Ta thế tọa độ M(0;1) và Q(2;−1) vào đường thẳng:

$\left( {0 - 2.1 + 3} \right)\left( {2 - 2.\left( { - 1} \right) + 3} \right) >0$ nên chọn C.

Đáp án cần chọn là: C

Ta thế tọa độ M(0;1) và P(0;2) vào đường thẳng:

$\left( {0 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0$ nên loại A.

Ta thế tọa độ N(1;1) và P(0;2) vào đường thẳng:

$\left( {1 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0$ nên loại B.

Ta thế tọa độ M(0;1) và Q(2;−1) vào đường thẳng:

$\left( {0 - 2.1 + 3} \right)\left( {2 - 2.\left( { - 1} \right) + 3} \right) > 0$ nên chọn C.

Đáp án cần chọn là: C

Đường thẳng (d) có VTPT$\overrightarrow {{n_1}} = \left( {3; - 4} \right)$

Đường thẳng $\left( {\rm{\Delta }} \right)$có VTPT$\overrightarrow {{n_2}} = \left( {a;b} \right)$

$\Rightarrow cos(d;\Delta ) = cos\left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{|3a - 4b|}}{{5\sqrt {{a^2} + {b^2}} }}$

$\Leftrightarrow cos{45^o} = \frac{{|3a - 4b|}}{{5\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \frac{{|3a - 4b|}}{{5\sqrt {{a^2} + {b^2}} }} = \frac{{\sqrt 2 }}{2}$

$\Leftrightarrow \sqrt 2 |3a - 4b| = 5\sqrt {{a^2} + {b^2}} \Leftrightarrow 2{(3a - 4b)^2} = 25({a^2} + {b^2})$

$\Leftrightarrow 7{a^2} + 48ab - 7{b^2} = 0(1)$

Mặt khác$M\left( {2; - 1} \right) \in {\rm{\Delta }} \Rightarrow 2a - b + 5 = 0 \Leftrightarrow b = 2a + 5$thế vào (1)

$\Rightarrow 7{a^2} + 48a(2a + 5) - 7{(2a + 5)^2} = 0 \Leftrightarrow 75{a^2} + 100a$

$- 175 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a = 1 \Rightarrow b = 7(tm)}\\{a = - \frac{7}{3} \Rightarrow b = \frac{1}{3}(ktm)}\end{array}} \right.$

$\Rightarrow a + b = 8.$

Đáp án cần chọn là: C

Ta thấy${d_1}:\,\,\,2x - y + 3 = 0;\,\,\,{d_2}:\,\,\,x + 2y - 5 = 0$là hai đường thẳng vuông góc.

Giả sử hình chữ nhật bài cho là ABCD có: 

$AB:\,\,\,2x - y + 3 = 0;\,\,\,AD:\,\,\,x + 2y - 5 = 0$

Thay tọa độ điểm (2;3) vào các phương trình đường thẳng AB,AD ta thấy (2;3) không thuộc các đường thẳng trên ⇒C(2;3).

$\Rightarrow {S_{ABCD}} = CB.CD = d(C;AB).d(C;AD)$

$\begin{array}{l} = \frac{{\left| {2.2 - 3 + 3} \right|}}{{\sqrt {{2^2} + {1^2}} }}.\frac{{\left| {2 + 2.3 - 5} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{4}{{\sqrt 5 }}.\frac{3}{{\sqrt 5 }} = \frac{{12}}{5}\,\,\,\left( {dvdt} \right)\\\end{array}$

Đáp án cần chọn là: D

Gọi $M\left( {0;m} \right) \in Oy;\,\,AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {6 - 2} \right)}^2}} = 5.$

Có ${S_{{\rm{\Delta }}MAB}} = \frac{1}{2}d\left( {M,AB} \right).AB \Leftrightarrow 1 = \frac{1}{2}.d\left( {M,AB} \right).5 \Leftrightarrow d\left( {M,AB} \right) = \frac{2}{5}$

$\overrightarrow {AB} = \left( {3;4} \right) \Rightarrow \vec n = \left( {4; - 3} \right)$ là 1 VTPT của  AB.

⇒ Phương trình AB: $4\left( {x - 1} \right) - 3\left( {y - 2} \right) = 0 \Leftrightarrow 4x - 3y + 2 = 0$$\Rightarrow d\left( {M,AB} \right) = \frac{{\left| { - 3m + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} \Leftrightarrow \frac{2}{5} = \frac{{\left| { - 3m + 2} \right|}}{5} \Leftrightarrow \left| { - 3m + 2} \right| = 2$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 3m + 2 = 2}\\{ - 3m + 2 = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0 \Rightarrow M(0;0)}\\{m = \frac{4}{3} \Rightarrow M\left( {0;\frac{4}{3}} \right)}\end{array}} \right.$

Đáp án cần chọn là: B

Khoảng cách từ điểm M (–2; 2) đến đường thẳng$\Delta :$$5x - 12y + 8 = 0$

$d\left( {M;{\rm{\Delta }}} \right) = \frac{{\left| { - 2.5 - 12.2 + 8} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{{26}}{{13}} = 2.$

Đáp án cần chọn là: B

${{\rm{\Delta }}_1}:\;\;3x + 4y = 12 \Leftrightarrow 3x + 4y - 12 = 0.$

Xét phương trình đường thẳng${{\rm{\Delta }}_1},\;{{\rm{\Delta }}_2}$ ta có:$\frac{3}{6} = \frac{4}{8} \ne - \frac{{12}}{{11}} \Rightarrow {{\rm{\Delta }}_1}//{{\rm{\Delta }}_2}.$

Chọn $A\left( {0;3} \right) \in {{\rm{\Delta }}_1}.$  Khi đó ta có:

$\Rightarrow d\left( {{{\rm{\Delta }}_1};{{\rm{\Delta }}_2}} \right) = d\left( {A;{{\rm{\Delta }}_2}} \right) = \frac{{\left| {24 - 11} \right|}}{{\sqrt {{6^2} + {8^2}} }} = \frac{{13}}{{10}} = 1,3.$

Đáp án cần chọn là: A

Phương trình đường thẳng BC là y=0, vì $M \in BC\;$ nên gọi M(m;0).

Ta có:$\overrightarrow {AM} = \left( {m - 2; - 3} \right)$ nên$\vec n = \left( {3;m - 2} \right)$ là 1 VTPT của đường thẳng AM.

Phương trình đường thẳng AM là:

$\begin{array}{*{20}{l}}{3\left( {x - 2} \right) + \left( {m - 2} \right)\left( {y - 3} \right) = 0}\\{ \Leftrightarrow 3x + \left( {m - 2} \right)y - 6 - 3m + 6 = 0}\\{ \Leftrightarrow 3x + \left( {m - 2} \right)y - 3m = 0}\end{array}$

$\begin{array}{*{20}{l}}{ \Rightarrow d\left( {B;AM} \right) = \frac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}}\\{\,\,\,\,\,\,d\left( {C;AM} \right) = \frac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}}\end{array}$

Ta có:

$\left\{ {\begin{array}{*{20}{c}}{{S_{\Delta MAB}} = \frac{1}{2}d(B;AM).AM}\\{{S_{\Delta MAC}} = \frac{1}{2}d(C;AM).AM}\end{array}} \right. \Rightarrow {S_{\Delta MAB}} = 2{S_{\Delta MAC}}$

$\Leftrightarrow d(B;AM) = 2d(C;AM)$

$\frac{{|15 - 3m|}}{{\sqrt {9 + {{(m - 2)}^2}} }} = 2\frac{{| - 3 - 3m|}}{{\sqrt {9 + {{(m - 2)}^2}} }}$

$\Leftrightarrow |15 - 3m| = 2| - 3 - 3m|$

$\left[ {\begin{array}{*{20}{c}}{15 - 3m = - 6 - 6m}\\{15 - 3m = 6 + 6m}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = - 7}\\{m = 1}\end{array}} \right.$

Vậy M(1;0) hoặc M(−7;0)

Đáp án cần chọn là: B

Đáp án cần chọn là: A