Các bài toán về đường thẳng và mặt cầu
-
442 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[(S):{x^2} + {(y + 1)^2} + {z^2} = {R^2}\]. Điều kiện của bán kính R để trục Ox tiếp xúc với (S) là:
 Xem đáp án
Xem đáp án
Tọa độ giao điểm của (S) và Ox là nghiệm của hệ\(\left\{ {\begin{array}{*{20}{c}}{{x^2} + {{(y + 1)}^2} + {z^2} = {R^2}}\\{x = t}\\{y = 0}\\{z = 0}\end{array}} \right.\left( * \right)\)
(S) tiếp xúc với Ox khi và chỉ khi (*) có nghiệm kép\[ \Leftrightarrow {t^2} + 1 = {R^2}\]có nghiệm kép
\[ \Leftrightarrow {R^2} - 1 = 0 \Leftrightarrow R = 1\]
Đáp án cần chọn là: D
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;−2;3) và đường thẳng d có phương trình \[\frac{{x + 1}}{2} = \frac{{y - 2}}{1} = \frac{{z + 3}}{{ - 1}}\]. Tính đường kính của mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d.
 Xem đáp án
Xem đáp án
Phương trình mặt cầu (S) có dạng\[{(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = {R^2}\]
Phương trình tham số của d là:\(\left\{ {\begin{array}{*{20}{c}}{x = - 1 + 2t}\\{y = 2 + t}\\{z = - 3 - t}\end{array}} \right.\)
Tọa độ giao điểm của (S) và d là nghiệm của hệ
\(\left\{ {\begin{array}{*{20}{c}}{{{(x - 1)}^2} + {{(y + 2)}^2} + {{(z - 3)}^2} = {R^2}}\\{x = - 1 + 2t}\\{y = 2 + t}\\{z = - 3 - t}\end{array}\left( * \right)} \right.\)
(S) tiếp xúc với dd khi và chỉ khi (∗) có nghiệm kép
\[ \Leftrightarrow {( - 2 + 2t)^2} + {(4 + t)^2} + {( - 6 - t)^2} = {R^2}\] có nghiệm kép
\[ \Leftrightarrow 6{t^2} + 12t + 56 - {R^2} = 0\] có nghiệm kép
\[ \Leftrightarrow {\rm{\Delta '}} = {\left( { - 6} \right)^2} - 6.(56 - {R^2}) = 0 \Leftrightarrow 6{R^2} - 300 = 0 \Leftrightarrow {R^2} = 50 \Leftrightarrow R = 5\sqrt 2 \]
Suy ra đường kính của mặt cầu (S) là\[10\sqrt 2 \]
Đáp án cần chọn là: B
Câu 3:
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng \[d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 2}}{1}\;\] là:
 Xem đáp án
Xem đáp án
Phương trình mặt cầu (S) có dạng \[{(x - 2)^2} + {y^2} + {(z - 1)^2} = {R^2}\]
Phương trình tham số của d là:\(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2t}\\{z = 2 + t}\end{array}} \right.\)
Tọa độ giao điểm của (S) và d là nghiệm của hệ
\(\left\{ {\begin{array}{*{20}{c}}{{{(x - 2)}^2} + {y^2} + {{(z - 1)}^2} = {R^2}}\\{x = 1 + t}\\{y = 2t}\\{z = 2 + t}\end{array}\left( * \right)} \right.\)
(S) tiếp xúc với dd khi và chỉ khi (∗) có nghiệm kép
\[ \Leftrightarrow {(t - 1)^2} + {(2t)^2} + {(1 + t)^2} = {R^2}\] có nghiệm kép
\[ \Leftrightarrow 6{t^2} + 2 = {R^2}\] có nghiệm kép\[ \Leftrightarrow {R^2} = 2\]
Đáp án cần chọn là: A
Câu 4:
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng \[d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 2}}{1}\] là:
 Xem đáp án
Xem đáp án
Phương trình mặt cầu (S) có dạng\[{(x - 2)^2} + {y^2} + {(z - 1)^2} = {R^2}\]
Phương trình tham số của d là:\(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2t}\\{z = 2 + t}\end{array}} \right.\)
Tọa độ giao điểm của (S) và d là nghiệm của hệ
\[{x^2} + {y^2} + {z^2} + x + y + z - 6 = 0\]\(\left\{ {\begin{array}{*{20}{c}}{{{(x - 2)}^2} + {y^2} + {{(z - 1)}^2} = {R^2}}\\{x = 1 + t}\\{y = 2t}\\{z = 2 + t}\end{array}\left( * \right)} \right.\)
(S) tiếp xúc với dd khi và chỉ khi (∗) có nghiệm kép
\[ \Leftrightarrow {(t - 1)^2} + {(2t)^2} + {(1 + t)^2} = {R^2}\] có nghiệm kép
\[ \Leftrightarrow 6{t^2} + 2 = {R^2}\] có nghiệm kép\[ \Leftrightarrow {R^2} = 2\]
Đáp án cần chọn là: A
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ có phương trình x=y=z. Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu không có hai điểm chung phân biệt với Δ là:
 Xem đáp án
Xem đáp án
\[A \in {\rm{\Delta }} \Rightarrow A\left( {t;t;t} \right)\]
- ThayA(t;t;t) vào\[{x^2} + {y^2} + {z^2} + x + y + z - 6 = 0\]ta có\[3{t^2} + 3t - 6 = 0\]
Phương trình có 2 nghiệm phân biệt. Loại
- Thay\[A\left( {t;t;t} \right)\]vào\[{x^2} + {y^2} + {z^2} + 2x - 4y + 2z - 3 = 0\]ta có\[3{t^2} - 3 = 0\]
Phương trình có 2 nghiệm phân biệt. Loại
- Thay\[A\left( {t;t;t} \right)\]vào\[{x^2} + {y^2} + {z^2} - 2x + 3y + 5z + 3 = 0\]ta có\[3{t^2} + 6t + 3 = 0\]
Phương trình có nghiệm kép. Thỏa mãn
- Thay\[A\left( {t;t;t} \right)\]vào\[{x^2} + {y^2} + {z^2} - 7x - 2z + 6 = 0\]ta có \[3{t^2} - 9t + 6 = 0\]
Phương trình có 2 nghiệm phân biệt. Loại
Đáp án cần chọn là: C
Câu 6:
Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu có điểm chung với trục Oz là:
 Xem đáp án
Xem đáp án
- ThayA(0;0;t) vào \[{x^2} + {y^2} + {z^2} + 4x - 8y + 2z + 2 = 0\]ta có\[{t^2} + 2t + 2 = 0\]
Phương trình vô nghiệm. Loại
- ThayA(0;0;t) vào \[{x^2} + {y^2} + {z^2} + 2x - 4y - 2z + 2 = 0\]ta có\[{t^2} - 2t + 2 = 0\]
Phương trình vô nghiệm. Loại
- ThayA(0;0;t) vào \[{x^2} + {y^2} + {z^2} + x - 2y + z + 1 = 0\]ta có\[{t^2} + t + 1 = 0\]
Phương trình vô nghiệm. Loại
- ThayA(0;0;t) vào \[{x^2} + {y^2} + {z^2} - 2x + 4y + 4z + 4 = 0\]ta có\[{t^2} + 4t + 4 = 0\]
Phương trình có nghiệm kép. Thỏa mãn
Đáp án cần chọn là: D
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình
\[{(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 50\]. Trong số các đường thẳng sau, mặt cầu (S) tiếp xúc với đường thẳng nào.
 Xem đáp án
Xem đáp án
(S) có tâm\[I(1; - 2;3)\] và\[R = \sqrt {50} \]
Gọi M là hình chiếu của I lên trục Ox.
Suy ra\[M(1;0;0) \Rightarrow d(I,{\rm{Ox}}) = {\rm{MI}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \ne R \Rightarrow \]loại B.
Gọi N là hình chiếu của I lên trục Oy.
Suy ra\[N(0; - 2;0) \Rightarrow d(I,{\rm{Oy) = NI = \;}}\sqrt {{1^2} + {3^2}} = \sqrt {10} \ne R \Rightarrow \]loại C
Gọi P là hình chiếu của I lên trục Oz.
Suy ra \[P(0;0;3) \Rightarrow d(I,{\rm{Oz}}) = {\rm{PI}} = \sqrt {{1^2} + {2^2}} = \sqrt 5 \ne R \Rightarrow \] loại D
Đáp án cần chọn là: ACâu 8. Xét đường thẳng d có phương trình \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2}\\{z = 3 + 2t}\end{array}} \right.\)và mặt cầu (S) có phương trình \[{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 4\]. Nhận xét nào sau đây đúng.
A.d cắt (S) tại hai điểm phân biệt A,B và AB<2R
B.d không có điểm chung với (S)
C.d tiếp xúc với (S)
D.d cắt (S) tại hai điểm phân biệt A,B và AB đạt GTLN.
Giải hệ:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2}\\{z = 3 + 2t}\\{{{(x - 1)}^2} + {{(y - 2)}^2} + {{(z - 3)}^2} = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2}\\{z = 3 + 2t}\\{{t^2} + {{(2t)}^2} = 4}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2}\\{z = 3 + 2t}\\{5{t^2} = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t = \pm \sqrt {\frac{4}{5}} }\\{x = 1 + t}\\{y = 2}\\{z = 3 + 2t}\end{array}} \right.\end{array}\)
Suy ra d cắt (S) tại hai điểm phân biệt.
Mặt khác (S) có tâm \[I(1;2;3) \in d\;\] nên d qua tâm của mặt cầu.
Do đó AB đạt GTLN.
Đáp án cần chọn là: D
Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[(S):{(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 9\] và đường thẳng \[d:x - 1 = \frac{{y - 2}}{2} = \frac{{z - 4}}{3}\]. (d) cắt (S) tại hai điểm phân biệt A và B. Khi đó AB bằng:
 Xem đáp án
Xem đáp án
Tham số hóa phương trình đường thẳng d ta được: d:\(\left\{ {\begin{array}{*{20}{c}}{x = t + 1}\\{y = 2 + 2t}\\{z = 4 + 3t}\end{array}} \right.\)
Giả sử A là giao điểm của (d) và (P).
Vì \[A \in d:\left\{ {\begin{array}{*{20}{c}}{x = t + 1}\\{y = 2 + 2t}\\{z = 4 + 3t}\end{array}} \right.\] nên ta có:\[A\left( {t + 1;2 + 2t;4 + 3t} \right)\]
Mặt khác\[A \in (S)\] nên ta có
\[{(t + 1 - 1)^2} + {(2 + 2t + 2)^2} + {(4 + 3t - 3)^2} = 9\]
\[ \Leftrightarrow {t^2} + {(4 + 2t)^2} + {(1 + 3t)^2} = 9\]
\[ \Leftrightarrow 14{t^2} + 22t + 8 = 0\]
\(\begin{array}{l} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = - \frac{4}{7}}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{A(0;0;1)}\\{B\left( {\frac{3}{7};\frac{6}{7};\frac{{16}}{7}} \right)}\end{array}} \right.\\ \Rightarrow AB = \sqrt {{{\left( {\frac{3}{7}} \right)}^2} + {{\left( {\frac{6}{7}} \right)}^2} + {{\left( {\frac{{16}}{7} - 1} \right)}^2}} = \frac{{\sqrt {126} }}{7}\end{array}\)
Đáp án cần chọn là: A
Câu 9:
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(3;−2;0) và cắt trục Oy tại hai điểm A,B mà AB=8 là
 Xem đáp án
Xem đáp án
Gọi H là hình chiếu vuông góc của I lên\[Oy \Rightarrow H(0; - 2;0)\]
\[ \Rightarrow \overrightarrow {IH} = \left( { - 3;0;0} \right) \Rightarrow IH = 3\]
Mặt khác ta có: \[AH = \frac{{AB}}{2} = 4\]
Suy ra\[{R^2} = A{H^2} + H{I^2} = {4^2} + {3^2} = 25\]
(S) có tâm I(3;−2;0) và bán kính R với \[{R^2} = 25\] Suy ra:
\[(S):{(x - 3)^2} + {(y + 2)^2} + {z^2} = 25\]
Đáp án cần chọn là: D
Câu 10:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 2t}\\{y = t}\\{z = t}\end{array}} \right.\)và \(d':\left\{ {\begin{array}{*{20}{c}}{x = t'}\\{y = 3 - t'}\\{z = 0}\end{array}} \right.\). Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d′ là:
 Xem đáp án
Xem đáp án
Lấy\[{\rm{A}} \in {\rm{d}} \Rightarrow {\rm{A}}\left( {2a;a;4} \right)\] và\[B \in d' \Rightarrow B\left( {b;3 - b;0} \right)\].
Ta có:\[\overrightarrow {AB} = \left( {b - 2a;3 - a - b; - 4} \right)\]
AB là đoạn vuông góc chung của hai đường thẳng d và d′ khi và chỉ khi
\(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {AB} .\overrightarrow {{u_d}} = 0}\\{\overrightarrow {AB} .\overrightarrow {{u_{d'}}} = 0}\end{array}} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2.(b - 2a) + 1.(3 - a - b) + 0.( - 4) = 0}\\{1.(b - 2a) - 1.(3 - a - b) + 0.( - 4) = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 5a + b + 3 = 0}\\{ - a + 2b - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = 2}\end{array}} \right.\end{array}\)
Suy ra \[{\rm{A}}\left( {2;1;4} \right);B\left( {2;1;0} \right)\] và\[\overrightarrow {AB} = \left( {0;0; - 4} \right)\]
Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d′
Có tâm I là trung điểm của AB và bán kính\[R = \frac{{AB}}{2}\]
Ta có I(2;1;2) và \[R = \frac{{AB}}{2} = \frac{4}{2} = 2\]
Vậy ta có\[{(x - 2)^2} + {(y - 1)^2} + {(z - 2)^2} = 4\]
Đáp án cần chọn là: C
Câu 11:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình \[{(x + 1)^2} + {(y - 1)^2} + {(z - 2)^2} = 4\]. Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz.
 Xem đáp án
Xem đáp án
Bước 1: Gọi (S′) là mặt cầu đối xứng với mặt cầu (S) qua trục Oz.
(S) có tâm I(−1;1;2) và R=2
Bước 2: Tìm J là điểm đối xứng của tâm mặt cầu (S) qua Oz.
Lấy đối xứng điểm I qua trục Oz ta được J(1;−1;2).
Bước 3: Tìm mặt cầu (S′)
(S′) có tâm J và bán kính R có phương trình là: \[{(x - 1)^2} + {(y + 1)^2} + {(z - 2)^2} = 4\]
Đáp án cần chọn là: A
Câu 12:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x−y−2z+1=0 và ba điểmA(1;−2;0), B(1;0;−1) và C(0;0;−2). Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB,AC,BC?
 Xem đáp án
Xem đáp án
Ta có:
\[\overrightarrow {AB} = \left( {0;2; - 1} \right)\]
\[\overrightarrow {AC} = \left( { - 1;2; - 2} \right)\]
\[\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 2;1;2} \right)\]
Mặt phẳng (ABC) có vecto pháp tuyến là\[\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 2;1;2} \right)\]Suy ra\[(P)//(ABC)\]
Trên mặt phẳng (ABC) có 4 điểm M,N,P,Q cách đều AB,BC,AC là tâm đường tròn nội tiếp, 3 tâm đường tròn bàng tiếp các góc A,B,C do đó có 4 điểm M′,N′,P′,Q′ trên mặt phẳng (P) là hình chiếu vuông góc của M,N,P,Q trên (P) thỏa mãn tính chất cách đều AB,BC,AC.
Tương ứng có 4 mặt cầu tâm M′,N′,P′,Q′ thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: A
Câu 13:
Trong không gian với hệ tọa độ Oxyz. Hãy viết phương trình mặt cầu (S) có tâm I(2;0;1) và tiếp xúc với đường thẳng \[d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 2}}{1}\].
 Xem đáp án
Xem đáp án
\[\overrightarrow {{u_d}} = (1;2;1)\] Lấy điểm\[M(1;0;2) \in d\]
\[\begin{array}{*{20}{l}}{\overrightarrow {MI} = ( - 1;0;1) \Rightarrow \left[ {\overrightarrow {MI} ,\vec u} \right] = ( - 2;2; - 2)}\\{R = d(I,d) = \frac{{\left| {\left[ {\overrightarrow {MI} ,\vec u} \right]} \right|}}{{\left| {\vec u} \right|}} = \frac{{\sqrt {{{(2)}^2} + {2^2} + {{( - 2)}^2}} }}{{\sqrt {{1^2} + {2^2} + {1^2}} }} = \sqrt 2 }\end{array}\]
Vậy phương trình mặt cầu tâm I(2;0;1) bán kính \(\sqrt 2 \) là:
\[{\left( {x - 2} \right)^2} + {y^2} + {\left( {z - 1} \right)^2} = 2\]
Đáp án cần chọn là: A
Câu 14:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\frac{{x - 1}}{{ - 1}} = \frac{{y - 2}}{1} = \frac{{z + 1}}{2}\], điểm A(2;−1;1). Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.
 Xem đáp án
Xem đáp án
Phương trình mặt phẳng (P) qua A , vuông góc (d) là:
\[ - 1.\left( {x - 2} \right) + 1.\left( {y + 1} \right) + 2.\left( {z - 1} \right) = 0 \Leftrightarrow - x + y + 2z + 1 = 0\]
Gọi \[I\left( {1 - t;2 + t; - 1 + 2t} \right) = d \cap \left( P \right)\] khi đó:
\[ - \left( {1 - t} \right) + \left( {2 + t} \right) + 2\left( { - 1 + 2t} \right) + 1 = 0 \Leftrightarrow t = 0 \Rightarrow I\left( {1;2; - 1} \right)\]
Có\[I{A^2} = 14\] Phương trình mặt cầu là:
\[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 14\]
Đáp án cần chọn là: D
Câu 15:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng \[\Delta :\frac{x}{1} = \frac{{y + 3}}{1} = \frac{z}{2}\;\]. Biết rằng mặt cầu (S) có bán kính bằng \(2\sqrt 2 \)và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính 2. Tìm tọa độ tâm I.
 Xem đáp án
Xem đáp án
Tâm I thuộc đường thẳng d nên\[I\left( {t; - 3 + t;2t} \right)\]
Phương trình mặt phẳng\[\left( {{\rm{Oxz}}} \right):y = 0\]
Ta có bán kính mặt cầu \[IM = 2\sqrt 2 \], mặt cầu cắt mặt phẳng (Oxz) theo đường tròn có bán kính HM=2 suy ra\[d\left( {I,\left( {Oxz} \right)} \right) = IH = \sqrt {I{M^2} - H{M^2}} = \sqrt {8 - 4} = 2\]
Ta có\[\left| { - 3 + t} \right| = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 3 + t = 2}\\{ - 3 + t = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 5 \Rightarrow I(5;2;10)}\\{t = 1 \Rightarrow I(1; - 2;2)}\end{array}} \right.\]
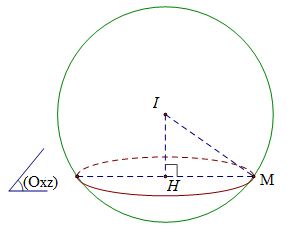
Đáp án cần chọn là: A
Câu 16:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình: \[{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0\] và đường thẳng \[\Delta :\frac{x}{2} = \frac{{y + 1}}{{ - 2}} = z\;\]. Mặt phẳng (P) vuông góc với Δ và tiếp xúc với (S) có phương trình là
 Xem đáp án
Xem đáp án
Tâm mặt cầu I(1;−2;1), bán kính R=3.
Mặt phẳng (P) vuông góc với \[{\rm{\Delta }}\] có phương trình dạng\[2{\rm{x}} - 2y + z + D = 0\]
Vì (P) tiếp xúc với mặt cầu nên\[d(I,(P)) = R \Rightarrow |D - 7| = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{D = - 2}\\{D = 16}\end{array}} \right.\]
Phương trình (P) là\[2x - 2y + z - 2 = 0;2x - 2y + z + 16 = 0\]
Đáp án cần chọn là: A
Câu 17:
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d:\(\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = - t}\\{z = - t}\end{array}} \right.\) và 2 mặt phẳng (P) và (Q) lần lượt có phương trình \[x + 2y + 2z + 3 = 0;x + 2y + 2z + 7 = 0\]. Viết phương trình mặt cầu (S) có tâmI thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P) và (Q).
 Xem đáp án
Xem đáp án
Ta có
\[\begin{array}{*{20}{l}}{I \in d \Rightarrow I\left( {t; - 1; - t} \right)}\\{ \Rightarrow d\left( {I,\left( P \right)} \right) = d\left( {I,\left( Q \right)} \right) \Leftrightarrow \frac{{\left| {t - 2 - 2t + 3} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \frac{{\left| {t - 2 - 2t + 7} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }}}\\{ \Leftrightarrow \left| { - t + 1} \right| = \left| { - t + 5} \right| \Leftrightarrow t = 3}\\{ \Rightarrow I\left( {3; - 1; - 3} \right)}\\{ \Rightarrow R = \frac{{\left| { - 3 + 1} \right|}}{{\sqrt 9 }} = \frac{2}{3}}\\{ \Rightarrow (S):{{\left( {x - 3} \right)}^2} + {{\left( {y + 1} \right)}^2} + {{\left( {z + 3} \right)}^2} = \frac{4}{9}}\end{array}\]
Đáp án cần chọn là: B
Câu 18:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\frac{x}{2} = \frac{{z - 3}}{1} = \frac{{y - 2}}{1}\;\] và hai mặt phẳng \[(P):x--2y + 2z = 0.(Q):x--2y + 3z - 5 = 0\]. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
 Xem đáp án
Xem đáp án
\[I \in d \Rightarrow I\left( {2t;3 + t;2 + t} \right)\]
\[I \in \left( P \right) \Rightarrow 2t - 2(3 + t) + 2(2 + t) = 0 \Leftrightarrow t = 1 \Rightarrow I\left( {2;4;3} \right)\]
Do (Q) tiếp xúc với mặt cầu (S)nên \[R = d\left( {I;\left( Q \right)} \right) = \frac{{|2 - 2.4 + 3.3 - 5|}}{{\sqrt {1 + {2^2} + {3^2}} }} = \sqrt {\frac{2}{7}} \]
\[ \Rightarrow \left( S \right):{\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z - 3} \right)^2} = \frac{2}{7}\]
Đáp án cần chọn là: C
Câu 19:
Trong không gian Oxyz, cho 3 điểm A(0;1;1),B(3;0;−1),C(0;21;−19) và mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\]. Điểm M thuộc mặt cầu (S) sao cho tổng \[3M{A^2} + 2M{B^2} + M{C^2}\;\] đạt giá trị nhỏ nhất, khi đó, độ dài vectơ \[\overrightarrow {OM} \;\] là
 Xem đáp án
Xem đáp án
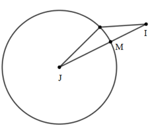
+) Mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 1\]có tâm J(1;1;1), bán kính R=1.
+) Tìm I: \[3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0 \Leftrightarrow 6\overrightarrow {IA} + 2\overrightarrow {AB} + \overrightarrow {AC} = \vec 0 \Leftrightarrow \overrightarrow {IA} = - \frac{{2\overrightarrow {AB} + \overrightarrow {AC} }}{6}\]
\[A\left( {0;1;1} \right),B\left( {3;0; - 1} \right),C\left( {0;21; - 19} \right)\]
\[ \Rightarrow \overrightarrow {IA} \left( { - {x_I};1 - {y_I};1 - {z_I}} \right),\overrightarrow {AB} \left( {3; - 1; - 2} \right),\overrightarrow {AC} \left( {0;20; - 20} \right)\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{ - {x_I} = - \frac{{2.3 + 0}}{6}}\\{1 - {y_I} = - \frac{{2.( - 1) + 20}}{6}}\\{1 - {z_I} = - \frac{{2.( - 2) + ( - 20)}}{6}}\end{array}} \right. \Rightarrow I(1;4; - 3)\)
+) Ta có:
\[\begin{array}{*{20}{l}}{3M{A^2} + 2M{B^2} + M{C^2}}\\{ = 3{{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)}^2} + 2{{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)}^2} + {{\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)}^2}}\\{ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}}\\{ + 2.\overrightarrow {MI} .\left( {3\overrightarrow {IA} + 2\overrightarrow {IB} + \overrightarrow {IC} } \right)}\\{ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2} + 2.\overrightarrow {MI} .\vec 0}\\{ = 6M{I^2} + 3I{A^2} + 2I{B^2} + I{C^2}}\end{array}\]
Để tổng trên là nhỏ nhất thì MI nhỏ nhất ⇒M là giao điểm của đoạn thẳng IJ và mặt cầu (S).
\[\overrightarrow {JI} = \left( {0;3; - 4} \right)\]=> Tọa độ điểm M thuộc đoạn IJ có dạng\[\left( {1;1 + 3t;1 - 4t} \right),t \in \left[ {0;1} \right]\]
Mặt khác\[M \in \left( S \right) \Rightarrow {\left( {1 - 1} \right)^2} + {\left( {1 - \left( {1 + 3t} \right)} \right)^2} + {\left( {1 - \left( {1 - 4t} \right)} \right)^2} = 1\]
\[ \Leftrightarrow {t^2} = \frac{1}{{25}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \frac{1}{5}}\\{t = - \frac{1}{5}\left( L \right)}\end{array}} \right. \Rightarrow t = \frac{1}{5} \Rightarrow M\left( {1;\frac{8}{5};\frac{1}{5}} \right) \Rightarrow OM = \frac{{3\sqrt {10} }}{5}\]
Đáp án cần chọn là: C
Câu 20:
Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng \[(P):2x + 2y - z - 3 = 0\]và mặt cầu \[(S):{(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\]. Gọi \[\Delta \] là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của \[\Delta \] là:
 Xem đáp án
Xem đáp án
Dễ thấy \[E \in \left( P \right)\]. Gọi I(3;2;5) là tâm khối cầu.
Đường thẳng qua I vuông góc với (P): \(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 2 + 2t}\\{z = 5 - t}\end{array}} \right.\left( d \right)\)
Gọi H là hình chiếu của I lên (P)\[ \Rightarrow H \in \left( d \right) \Rightarrow H\left( {3 + 2t;2 + 2t;5 - t} \right)\]
Lại có\[H \in \left( P \right)\]
\[\begin{array}{*{20}{l}}{ \Rightarrow 2\left( {3 + 2t} \right) + 2\left( {2 + 2t} \right) - 5 + t - 3 = 0}\\{ \Leftrightarrow 6 + 4t + 4 + 4t - 5 + t - 3 = 0}\\{ \Leftrightarrow 9t + 2 = 0 \Leftrightarrow t = \frac{{ - 2}}{9} \Rightarrow H\left( {\frac{{23}}{9};\frac{{14}}{9};\frac{{47}}{9}} \right)}\\{ \Rightarrow \overrightarrow {EH} \left( {\frac{5}{9};\frac{5}{9};\frac{{20}}{9}} \right) = \frac{5}{9}\left( {1;\;1;\;4} \right)//\left( {1;1;4} \right) = \vec a}\end{array}\]
Để đường thẳng \[\left( {\rm{\Delta }} \right)\]cắt mặt cầu (S) tại 2 điểm sao cho chúng có khoảng cách nhỏ nhất thì đường thẳng \[\left( {\rm{\Delta }} \right)\]đi qua E và vuông góc với HE.
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{u_\Delta }} \bot \overrightarrow {{n_P}} }\\{\overrightarrow {{u_\Delta }} \bot \overrightarrow a }\end{array}} \right. \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{n_P}} ;\overrightarrow a } \right]\)
\( = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&4\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&2\\4&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&2\\1&1\end{array}} \right|} \right) = (9; - 9;0) = 9(1; - 1;0)\)
Vậy đường thẳng \[\left( {\rm{\Delta }} \right)\]đi qua E và nhận (1;−1;0) là 1 VTCP.
Vậy phương trình đường thẳng\(\left( \Delta \right):\left\{ {\begin{array}{*{20}{c}}{x = 2 + t}\\{y = 1 - t}\\{z = 3}\end{array}} \right.\)
Đáp án cần chọn là: C
Câu 21:
Trong không gian Oxyz, cho điểm S(−2;1;−2) nằm trên mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} = 9\]. Từ điểm S kẻ ba dây cung SA,SB,SC với mặt cầu (S) có độ dài bằng nhau và đôi một tạo với nhau góc 600. Dây cung AB có độ dài bằng:
 Xem đáp án
Xem đáp án
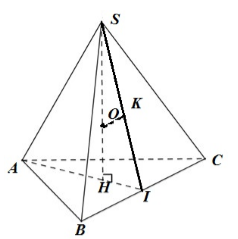
Xét tứ diện SABC có: \[SA = SB = SC,\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {60^0} \Rightarrow SABC\] là tứ diện đều.
Mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} = 9\]có tâm O, bán kính R=3, ngoại tiếp khối tứ diện SABC\[ \Rightarrow OS = OA = OB = OC = 3\]
Giả sử độ dài dây AB là a \[ \Rightarrow \,SI = AI = \frac{{a\sqrt 3 }}{2} \Rightarrow \,AH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\]
\[ \Rightarrow SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{a^2} - \frac{1}{3}{a^2}} = \sqrt {\frac{2}{3}} a\]
\[ \Rightarrow R = \frac{{{a^2}}}{{2\sqrt {\frac{2}{3}} a}} = \frac{{\sqrt 6 a}}{4} \Rightarrow \frac{{\sqrt 6 a}}{4} = 3 \Leftrightarrow a = 2\sqrt 6 \]
Đáp án cần chọn là: A
Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;−2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.
 Xem đáp án
Xem đáp án
Khoảng cách từ tâm I đến trục Oz là: \[d\left( {I;\left( {Oz} \right)} \right) = \sqrt {{3^2} + {4^2}} = 5.\]
Vì tiếp xúc với trục Oz nên bán kính mặt cầu R=5.
Vậy phương trình cần tìm là
\[\left( S \right):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 2} \right)^2} = 25.\]
Đáp án cần chọn là: A
Câu 23:
Trong không gian Oxyz, cho hai mặt phẳng \[(\alpha ):x - my + z + 6m + 3 = 0\;\]và \[(\beta ):mx + y - mz + 3m - 8 = 0\]; hai mặt phẳng này cắt nhau theo giao tuyến là đường thẳng \[\Delta \]. Gọi \[\Delta '\] là hình chiếu của \[\Delta \] lên mặt phẳng Oxy. Biết rằng khi m thay đổi thì đường thẳng \[\Delta '\] luôn tiếp xúc với một mặt cầu cố định có tâm I(a;b;c) thuộc mặt phẳng OxyOxy. Tính giá trị biểu thức \[P = 10{a^2} - {b^2} + 3{c^2}.\]
 Xem đáp án
Xem đáp án
Bước 1: Biểu diễn M và vectơ chỉ phương của \(\Delta \) theo m.
Mặt phẳng\[(\alpha ):x - my + z + 6m - 3z = 0\] có một vectơ pháp tuyến là
\[\overrightarrow {{n_1}} = (1; - m;1)\], và mặt phẳng\[(\beta ):mx + y - mz + 3m - 8 = (\alpha ) \cap (\beta )\]
\[\overrightarrow {{n_1}} = (1; - m;1)\], và mặt phẳng\[(\beta ):mx + y - mz\] có một vectơ pháp tuyến là
\[\overrightarrow {{n_2}} = (m;1; - m).\] Ta có\[M\left( { - 3m + \frac{4}{m} - 3;0; - 3m - \frac{4}{m}} \right) \in {\rm{\Delta }} = \left( \alpha \right) \cap \left( \beta \right)\]
Do đó Δ có một vectơ chỉ phương là\[\vec u = \left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \left( {{m^2} - 1;2m;{m^2} + 1} \right)\]
Bước 2: Gọi (P) là mặt phẳng chứa đường thẳng Δ và vuông góc với mặt phẳng (Oxy). Tìm c.
Gọi (P) là mặt phẳng chứa đường thẳng Δ và vuông góc với mặt phẳng (Oxy). Khi đó (P) có một vectơ pháp tuyến là\[\vec n = [\vec u;\vec k] = \left( {2m;1 - {m^2};0} \right)\]
Phương trình mặt phẳng (P) là :\[2mx + \left( {1 - {m^2}} \right)y + 6{m^2} + 6m - 8 = 0\]
Vì\[I(a;b;c) \in (Oxy)\] nên I(a;b;0).
Bước 3: Theo giả thiết ta suy ra (P) là tiếp diện của mặt cầu \[(S) \Rightarrow d(I;(P)) = R\]. Tìm a và b
Theo giả thiết ta suy ra (P) là tiếp diện của mặt cầu\[(S) \Rightarrow d(I;(P)) = R\]
\[ \Leftrightarrow \frac{{\left| {2ma + \left( {1 - {m^2}} \right)b + 6{m^2} + 6m - 8} \right|}}{{\sqrt {4{m^2} + {{\left( {1 - {m^2}} \right)}^2}} }} = R > 0\]
\[ \Leftrightarrow \frac{{\left| {2m(a + 3) + (6 - b){m^2} + b - 8} \right|}}{{{m^2} + 1}} = R > 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2m(a + 3) + (6 - b){m^2} + b - 8 = R({m^2} + 1)}\\{2m(a + 3) + (6 - b){m^2} + b - 8 = - R({m^2} + 1)}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{2(a + 3) = 0}\\{6 - b = R}\\{b - 8 = R}\\{R > 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{2(a + 3) = 0}\\{6 - b = - R}\\{b - 8 = - R}\\{R > 0}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{a = - 3 = 0}\\{6 - b = b - 8}\\{ - R = 6 - b < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{a = - 3}\\{6 - b = b - 8}\\{R = 6 - b > 0}\end{array}} \right.}\end{array}} \right.\)</>
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 3}\\{b = 7}\end{array}} \right.\)
Vậy I(−3;7;0), do đó \[P = 10{a^2} - {b^2} + 3{c^2} = 41\]
