Logarit
-
529 lượt thi
-
43 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Logarit cơ số a của b kí hiệu là:
 Xem đáp án
Xem đáp án
Số logab được gọi là lôgarit cơ số a của b.
Đáp án cần chọn là: A
Câu 2:
Điều kiện để logab có nghĩa là:
 Xem đáp án
Xem đáp án
Điều kiện để \[{\log _a}b\] có nghĩa là \[0 < a \ne 1,b > 0\].
Đáp án cần chọn là: C
Câu 3:
Cho \[a > 0;a \ne 1,b > 0\], khi đó nếu \[lo{g_a}b = N\;\] thì:
 Xem đáp án
Xem đáp án
Cho \[a > 0;a \ne 1,b > 0\] khi đó nếu \[{\log _a}b = N\] thì\[{a^N} = b\]
Đáp án cần chọn là: C
Câu 4:
Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Ta có: \[{\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c(0 < a \ne 1;b,c > 0)\]
\[{\log _a}\left( {\frac{b}{c}} \right) = {\log _a}b - {\log _a}c(0 < a \ne 1;b,c > 0)\]
Đáp án cần chọn là: D
Câu 5:
Chọn công thức đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 6:
Với điều kiện các biểu thức đều có nghĩa, đẳng thức nào dưới đây không đúng?
 Xem đáp án
Xem đáp án
Ta có:
\[{\log _a}{b^n} = n{\log _a}b(0 < a \ne 1;b > 0)\]
\[{\log _a}\frac{1}{b} = - {\log _a}b(0 < a \ne 1;b > 0)\]
\[{\log _a}\sqrt[n]{b} = {\log _a}{b^{\frac{1}{n}}} = \frac{1}{n}{\log _a}b(0 < a \ne 1;b > 0;n > 0;n \in {N^ * })\]
Vậy đẳng thức không đúng là \[{\log _a}\sqrt[n]{b} = - n{\log _a}b\]
Đáp án cần chọn là: D
Câu 7:
Nếu a > 1 và b > c > 0 thì:
 Xem đáp án
Xem đáp án
Nếu a > 1 và b > c > 0 thì \[{\log _a}b > {\log _a}c\].
Đáp án cần chọn là: A
Câu 8:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
\[{\log _a}1 = 0\]nên A, C sai.
\[{\log _a}a = 1\]nên B sai, D đúng.
Đáp án cần chọn là: D
Câu 9:
Cho \[0 < a \ne 1,b > 0\]. Chọn mệnh đề sai:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 10:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 11:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 12:
Với điều kiện các logarit đều có nghĩa, chọn công thức biến đổi đúng:
 Xem đáp án
Xem đáp án
Từ công thức \[{\log _a}b.{\log _b}c = {\log _a}c \Leftrightarrow {\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}(0 < a,b \ne 1;c > 0)\] ta thấy chỉ có đáp án A đúng.
Đáp án cần chọn là: A
Câu 13:
Chọn đẳng thức đúng:
 Xem đáp án
Xem đáp án
Áp dụng công thức \[{\log _a}b = \frac{1}{{{{\log }_b}a}} \Leftrightarrow {\log _a}b.{\log _b}a = 1(0 < a,b \ne 1)\] ta được:
\[{\log _2}3 = \frac{1}{{{{\log }_3}2}}\] nên D đúng.
Đáp án cần chọn là: D
Câu 14:
Với điều kiện các biểu thức đều có nghĩa, chọn đẳng thức đúng:
 Xem đáp án
Xem đáp án
Ta có:
\[{\log _{{a^n}}}b = \frac{1}{n}{\log _a}b;{\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\] nên \[{\log _{{a^n}}}b = {\log _a}\sqrt[n]{b}\] (C đúng)
Mặt khác:\[{\log _{{a^n}}}b = \frac{1}{n}{\log _a}b;{\log _{{b^n}}}a = \frac{1}{n}{\log _b}a\] nên các đáp án A, B, D đều sai.
Đáp án cần chọn là: C
Câu 15:
Giá trị \[{\log _{\frac{1}{{\sqrt 3 }}}}81\] là:
 Xem đáp án
Xem đáp án
Ta có: \[{\log _{\frac{1}{{\sqrt 3 }}}}81 = {\log _{{{\sqrt 3 }^{ - 1}}}}{3^4} = - {\log _{\sqrt 3 }}{3^4}\]
\[ = - {\log _{{3^{\frac{1}{2}}}}}{3^4} = - \frac{1}{{1/2}}{\log _3}{3^4} = - 2{\log _3}{3^4} = - 2.4 = - 8\]
Đáp án cần chọn là: B
Câu 16:
Giá trị biểu thức \[{\log _a}\sqrt {a\sqrt {a\sqrt[3]{a}} } \] là:
 Xem đáp án
Xem đáp án
Ta có:
\[{\log _a}\sqrt {a\sqrt {a\sqrt[3]{a}} } = {\log _a}\sqrt {a\sqrt {a.{a^{\frac{1}{3}}}} } = {\log _a}\sqrt {a\sqrt {{a^{\frac{4}{3}}}} } = {\log _a}\sqrt {a.{a^{\frac{2}{3}}}} \]
\[ = {\log _a}\sqrt {{a^{\frac{5}{3}}}} = {\log _a}{a^{\frac{5}{6}}} = \frac{5}{6}\]
Đáp án cần chọn là: D
Câu 17:
Giá trị \[{\log _3}a\] âm khi nào?
 Xem đáp án
Xem đáp án
Vì 3 > 1 nên để\[{\log _3}a < 0\] thì 0 < a < 1.
Đáp án cần chọn là: A
Câu 18:
Với a và b là hai số thực dương tùy ý, \[\log \left( {a{b^2}} \right)\] bằng
 Xem đáp án
Xem đáp án
Ta có:\[\log \left( {a{b^2}} \right) = \log a + \log {b^2} = \log a + 2\log b\]
Đáp án cần chọn là: B
Câu 19:
Với các số thực a,b>0 bất kì; rút gọn biểu thức \(P = 2{\log _2}a - {\log _{\frac{1}{2}}}{b^2}\)
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 20:
Cho các số thực dương a,b với \[a \ne 1\]. Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 21:
Cho số thực xx thỏa mãn \[lo{g_2}\left( {lo{g_8}x} \right) = lo{g_8}\left( {lo{g_2}x} \right).\] Tính giá trị của \[P = {(lo{g_2}x)^2}\]
 Xem đáp án
Xem đáp án
Điều kiện xác định:\(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{lo{g_2}x > 0}\\{lo{g_8}x > 0}\end{array}} \right.\)
Khi đó:
\[{\log _2}\left( {{{\log }_8}x} \right) = {\log _8}\left( {{{\log }_2}x} \right) \Leftrightarrow {\log _2}\left( {\frac{1}{3}{{\log }_2}x} \right) = {\log _2}\sqrt[3]{{\left( {{{\log }_2}x} \right)}}\]
\[ \Leftrightarrow \frac{1}{3}{\log _2}x = \sqrt[3]{{\left( {{{\log }_2}x} \right)}} \Leftrightarrow \frac{1}{{27}}\log _2^3x = {\log _2}x \Leftrightarrow {\left( {{{\log }_2}x} \right)^2} = 27\]
(vì \[{\log _2}x > 0\] nên chia cả hai vế cho \[{\log _2}x \ne 0\]
Đáp án cần chọn là: D
Câu 22:
Trong các khẳng định dưới đây, khẳng định nào sai?
 Xem đáp án
Xem đáp án
\[{\log _{0.5}}a > {\log _{0.5}}b \Leftrightarrow a < b\] suy ra A sai.
\[\log x < 0 \Leftrightarrow \log x < \log 1 \Leftrightarrow 0 < x < 1\] suy ra B đúng.
\[{\log _2}x > 0 \Leftrightarrow {\log _2}x > {\log _2}1 \Leftrightarrow x > 1\] suy ra C đúng.
\[{\log _{\frac{1}{3}}}a = {\log _{\frac{1}{3}}}b \Leftrightarrow a = b > 0\] suy ra D đúng.
Đáp án cần chọn là: A
Câu 23:
Cho a,ba,b là các số thực dương, thỏa mãn \[{a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\] và \[lo{g_b}\frac{1}{2} < lo{g_b}\frac{2}{3}\]. Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Ta có
\[\frac{3}{4} < \frac{4}{5}\] và \[{a^{\frac{3}{4}}} > {a^{\frac{4}{5}}} \Rightarrow 0 < a < 1\]
\[\frac{1}{2} < \frac{2}{3}\] và \[{\log _b}\frac{1}{2} < {\log _b}\frac{2}{3} \Rightarrow b > 1\]</>
Đáp án cần chọn là: C
Câu 24:
Cho hai số thực a và b , với 1<a
 Xem đáp án
Xem đáp án
Ta có:\[{\log _a}b > {\log _a}a = 1;{\log _b}a < {\log _b}b = 1 \Rightarrow {\log _b}a < 1 < {\log _a}b\]
Đáp án cần chọn là: D
Câu 25:
Cho \[0 < x < 1;0 < a;b;c \ne 1\]và \[lo{g_c}x > 0 > lo{g_b}x > lo{g_a}x\;\] so sánh a;b;ca;b;c ta được kết quả:
 Xem đáp án
Xem đáp án
Vì\[0 < x < 1 \Rightarrow \ln x < 0\] Do đó
\[{\log _c}x > 0 > {\log _b}x > {\log _a}x \Leftrightarrow \frac{{\ln x}}{{\ln c}} > 0 > \frac{{\ln x}}{{\ln b}} > \frac{{\ln x}}{{\ln a}}\]
\[ \Rightarrow \ln c < 0 < \ln a < \ln b\]
Mà hàm số\[y = \ln x\] đồng biến trên\[\left( {0; + \infty } \right)\] nên ta suy ra\[c < a < b\]
Đáp án cần chọn là: D
Câu 26:
Đặt \[{\log _2}3 = a;{\log _2}5 = b\]. Hãy biểu diễn \[P = lo{g_3}240\;\] theo a và b.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 27:
Đặt \[a = {\log _2}3,b = {\log _5}3\]. Hãy biểu diễn \[lo{g_6}45\;\] theo a và b:
 Xem đáp án
Xem đáp án
Có\[a = {\log _2}3 \Rightarrow {\log _3}2 = \frac{1}{a};b = {\log _5}3 \Rightarrow {\log _3}5 = \frac{1}{b}\]
\[{\log _6}45 = \frac{{{{\log }_3}45}}{{{{\log }_3}6}} = \frac{{{{\log }_3}\left( {{3^2}.5} \right)}}{{{{\log }_3}\left( {2.3} \right)}} = \frac{{2 + {{\log }_3}5}}{{{{\log }_3}2 + 1}} = \frac{{2 + \frac{1}{b}}}{{\frac{1}{a} + 1}} = \frac{{2ab + a}}{{ab + b}}\]
Đáp án cần chọn là: C
Câu 28:
Nếu \[{\log _{12}}18 = a\] thì \[lo{g_2}3\;\] bằng:
 Xem đáp án
Xem đáp án
Đăt \[{\log _2}3 = x\] Ta có
\[\begin{array}{*{20}{l}}{a = {{\log }_{12}}18 = \frac{{{{\log }_2}18}}{{{{\log }_2}12}} = \frac{{{{\log }_2}\left( {{{2.3}^2}} \right)}}{{{{\log }_2}\left( {{2^2}.3} \right)}} = \frac{{1 + 2{{\log }_2}3}}{{2 + {{\log }_2}3}} = \frac{{1 + 2x}}{{2 + x}}}\\{ \Rightarrow a\left( {2 + x} \right) = 1 + 2x \Rightarrow x\left( {a - 2} \right) = 1 - 2a}\\{ \Rightarrow {{\log }_2}3 = x = \frac{{1 - 2a}}{{a - 2}}}\end{array}\]
Đáp án cần chọn là: D
Câu 29:
Cho \[{\log _2}14 = a\]. Tính l\[lo{g_{49}}32\] theo a.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 30:
Đặt \[{\log _2}60 = a;{\log _5}15 = b.\]. Tính \[P = lo{g_2}12\] theo a và b.
 Xem đáp án
Xem đáp án
\[a = lo{g_2}60 = lo{g_2}({2^2}.15) = 2 + lo{g_2}15 \Rightarrow lo{g_2}15 = a - 2\]
\[ \Rightarrow lo{g_2}5 = \frac{{lo{g_{15}}5}}{{lo{g_{15}}2}} = \frac{{lo{g_2}15}}{{lo{g_5}15}} = \frac{{a - 2}}{b}\]
\[b = lo{g_5}15 = lo{g_5}(3.5) = 1 + lo{g_5}3 \Rightarrow lo{g_5}3 = b - 1\]
\[lo{g_2}3 = lo{g_2}5.lo{g_5}3 = \frac{{a - 2}}{b}.(b - 1) = \frac{{ab - 2b - a + 2}}{b}\]
\[lo{g_2}12 = lo{g_2}({2^2}.3) = 2 + lo{g_2}3 = \frac{{ab - a + 2}}{b}\]
Đáp án cần chọn là: B
Câu 31:
Đặt \[a = {\log _2}5\] và \(b = {\log _2}6\). Hãy biểu diễn \[lo{g_3}90\] theo a và b?
 Xem đáp án
Xem đáp án
Có \[b = {\log _2}6 = 1 + {\log _2}3 \Rightarrow {\log _2}3 = b - 1\]
\[\begin{array}{l}{\log _3}90 = {\log _3}({3^2}.2.5) = 2 + {\log _3}2 + {\log _3}5 = 2 + \frac{1}{{{{\log }_2}3}} + \frac{{{{\log }_2}5}}{{{{\log }_2}3}} = 2 + \frac{{1 + {{\log }_2}5}}{{{{\log }_2}3}}\\ = 2 + \frac{{1 + a}}{{b - 1}} = \frac{{a + 2b - 1}}{{b - 1}}\end{array}\]Đáp án cần chọn là: B
Câu 32:
Nếu \[{\log _a}b = p\] thì \[{\log _a}{a^2}{b^4}\;\] bằng:
 Xem đáp án
Xem đáp án
Ta có: \[{\log _a}{a^2}{b^4} = {\log _a}{a^2} + {\log _a}{b^4} = 2{\log _a}a + 4{\log _a}b = 2 + 4p\]
Đáp án cần chọn là: B
Câu 33:
Đặt \[a = {\log _3}4,b = {\log _5}4\]. Hãy biểu diễn \[lo{g_{12}}80\] theo a và b
 Xem đáp án
Xem đáp án
Ta có\[80 = {4^2}.5;12 = 3.4\]
\[\begin{array}{*{20}{l}}{{{\log }_{12}}80 = {{\log }_{12}}{4^2} + {{\log }_{12}}5 = 2{{\log }_{12}}4 + {{\log }_{12}}5 = \frac{2}{{{{\log }_4}12}} + \frac{1}{{{{\log }_5}12}} = \frac{2}{{{{\log }_4}3 + 1}} + \frac{1}{{{{\log }_5}3 + {{\log }_5}4}}}\\{ = \frac{2}{{\frac{1}{a} + 1}} + \frac{1}{{\frac{b}{a} + b}} = \frac{{2a}}{{a + 1}} + \frac{a}{{b\left( {a + 1} \right)}} = \frac{{2ab + a}}{{ab + b}}}\end{array}\]
Đáp án cần chọn là: C
Câu 34:
Nếu \[{\log _{12}}6 = a;{\log _{12}}7 = b\] thì:
 Xem đáp án
Xem đáp án
Gán giá trị đề bài cho bằng cách bấm:
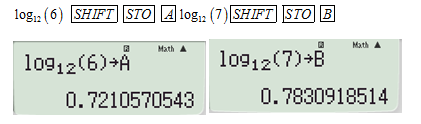
Lần lượt thử từng đáp án:
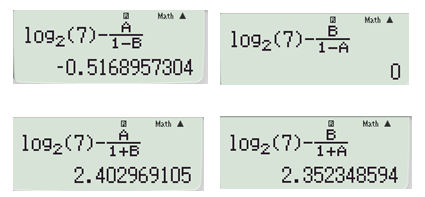
Đáp án cần chọn là: B
Câu 35:
Cho \[a > 0,b > 0\;\] thỏa mãn \[{a^2} + 4{b^2} = 5ab\]. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có: \[{a^2} + 4{b^2} = 5ab \Leftrightarrow {a^2} + 4ab + 4{b^2} = 9ab \Leftrightarrow {\left( {a + 2b} \right)^2} = 9ab\]
Logarit cơ số 1010 hai vế ta được:
\[\begin{array}{*{20}{l}}{\log {{\left( {a + 2b} \right)}^2} = \log \left( {9ab} \right) \Leftrightarrow 2\log \left( {a + 2b} \right) = \log 9 + \log a + \log b}\\{ \Leftrightarrow 2\log \left( {a + 2b} \right) = 2\log 3 + \log a + \log b \Leftrightarrow 2\left( {\log \left( {a + 2b} \right) - \log 3} \right) = \log a + \log b}\\{ \Leftrightarrow \log \frac{{a + 2b}}{3} = \frac{{\log a + \log b}}{2}}\end{array}\]
Đáp án cần chọn là: C
Câu 36:
Biết \[{\log _{15}}20 = a + \frac{{2{{\log }_3}2 + b}}{{{{\log }_3}5 + c}}\] với a\[a,b,c \in \mathbb{Z}\]. Tính \[T = a + b + c\]
 Xem đáp án
Xem đáp án
Ta có:
\[lo{g_{15}}20 = lo{g_{15}}({2^2}.5)\]
\[ = 2lo{g_{15}}2 + lo{g_{15}}5\]
\[ = \frac{2}{{lo{g_2}15}} + \frac{1}{{lo{g_5}15}}\]
\[ = \frac{2}{{lo{g_2}3 + lo{g_2}5}} + \frac{1}{{lo{g_5}3 + lo{g_5}5}}\]
\[ = \frac{2}{{\frac{1}{{lo{g_3}2}} + \frac{{lo{g_3}5}}{{lo{g_3}2}}}} + \frac{1}{{lo{g_5}3 + 1}}\]
\[ = \frac{{2lo{g_3}2}}{{1 + lo{g_3}5}} + \frac{1}{{\frac{1}{{lo{g_3}5}} + 1}}\]
\[ = \frac{{2lo{g_3}2}}{{1 + lo{g_3}5}} + \frac{{lo{g_3}5}}{{lo{g_3}5 + 1}}\]
\[ = \frac{{2lo{g_3}2 + lo{g_3}5}}{{lo{g_3}5 + 1}}\]
\[ = \frac{{lo{g_3}5 + 1 + 2lo{g_3}2 - 1}}{{lo{g_3}5 + 1}}\]
\[ = 1 + \frac{{2lo{g_3}2 - 1}}{{lo{g_3}5 + 1}}\]
\[ \Rightarrow a = 1,\,\,b = - 1,\,\,c = 1\]
Vậy \[T = a + b + c = 1 + \left( { - 1} \right) + 1 = 1.\]
Đáp án cần chọn là: D
Câu 37:
Cho biểu\[P = \,{(\ln a\, + {\log _a}e)^2}\, + {\ln ^2}a - \log _a^2e\], với a là số dương khác 1. Mệnh đề nào dưới đây đúng ?
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{P = {{\left( {\ln a + {{\log }_a}e} \right)}^2} + {{\ln }^2}a - \log _a^2e = {{\ln }^2}a + 2.\ln a.{{\log }_a}e + \log _a^2e + {{\ln }^2}a - \log _a^2e}\\{ = 2.{{\ln }^2}a + 2.\ln a.\frac{{\ln e}}{{\ln a}} = 2{{\ln }^2}a + 2}\end{array}\]
Đáp án cần chọn là: B
Câu 38:
Cho các số dương a,b,c,d. Biểu thức \[S = \ln \frac{a}{b} + \ln \frac{b}{c} + \ln \frac{c}{d} + \ln \frac{d}{a}\] bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 39:
Cho \[\log x = a\] và ln10=b . Tính \[lo{g_{10e}}x\] theo a và b
 Xem đáp án
Xem đáp án
Ta có:
\[{\log _{10e}}x = \frac{1}{{{{\log }_x}10e}} = \frac{1}{{{{\log }_x}e + {{\log }_x}10}} = \frac{1}{{\frac{{\ln e}}{{\ln x}} + \frac{{\ln 10}}{{\ln x}}}} = \frac{{\ln x}}{{1 + \ln 10}} = \frac{{\ln 10.\log x}}{{1 + \ln 10}}\]
Suy ra\[{\log _{10e}}x = \frac{{ab}}{{1 + b}}\]
Đáp án cần chọn là: B
Câu 40:
Sự tăng trưởng của 1 loài vi khuẩn được tính theo công thức \[S = A.{e^{rt}}\], trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r>0), tt là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 150 con và sau 5 giờ có 450 con, tìm số lượng vi khuẩn sau 10 giờ tăng trưởng.
 Xem đáp án
Xem đáp án
Ta có: \[450 = 150.{e^{5r}}\]
\[ = > {e^{5r}} = 3 \Leftrightarrow 5r = \ln 3 = > r = \frac{{\ln 3}}{5}\]
Số lượng vi khuẩn sau 10 giờ tăng trưởng là:
\[S = 150.{e^{10.\frac{{\ln 3}}{5}}} = 150.{\left( {{e^{\ln 3}}} \right)^2} = {150.3^2} = 1350\] (con)
Đáp án cần chọn là: B
Câu 41:
Cho a,b là các số dương thỏa mãn \[{a^2} + 4{b^2} = 12ab\]. Chọn khẳng định đúng trong các khẳng định sau:
 Xem đáp án
Xem đáp án
\[{a^2} + 4{b^2} = 12ab \Leftrightarrow {(a + 2b)^2} - 4ab = 12ab \Leftrightarrow {(a + 2b)^2} = 16ab\]
\[ \Rightarrow ln{(a + 2b)^2} = ln(16ab)\]
\[ \Rightarrow 2ln(a + 2b) = ln16 + lna + lnb\]
\[ \Rightarrow 2ln(a + 2b) - 4ln2 = lna + lnb\]
\[ \Rightarrow ln(a + 2b) - 2ln2 = \frac{1}{2}(lna + lnb)\]
Đáp án cần chọn là: C
Câu 42:
Cho \[a > 0,\,\,b > 0\] và \[ln\frac{{a + b}}{3} = \frac{{2lna + lnb}}{3}\]. Chọn mệnh đề đúng trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
\[ln\frac{{a + b}}{3} = \frac{{2lna + lnb}}{3}\]
\[ \Leftrightarrow 3ln\frac{{a + b}}{3} = 2lna + lnb\]
\[ \Leftrightarrow ln{(\frac{{a + b}}{3})^3} = ln{a^2} + lnb\]
\[ \Leftrightarrow ln\frac{{{{(a + b)}^3}}}{{27}} = ln({a^2}b)\]
\[ \Leftrightarrow \frac{{{{(a + b)}^3}}}{{27}} = {a^2}b\]
\[ \Leftrightarrow {(a + b)^3} = 27{a^2}b\]
\[ \Leftrightarrow {a^3} + 3{a^2}b + 3a{b^2} + {b^3} = 27{a^2}b\]
\[ \Leftrightarrow {a^3} + {b^3} = 24{a^2}b - 3a{b^2}\]
\[ \Leftrightarrow {a^3} + {b^3} = 3(8{a^2}b - a{b^2})\]
Đáp án cần chọn là: D
Câu 43:
Cho lnx=2. Tính giá trị của biểu thức \[T = 2ln\sqrt {ex} - ln\frac{{{e^2}}}{{\sqrt x }} + ln3.lo{g_3}e{x^2}\] ?
 Xem đáp án
Xem đáp án
Ta có
\[T = 2ln\sqrt {ex} - ln\frac{{{e^2}}}{{\sqrt x }} + ln3.lo{g_3}e{x^2}\]
\[ = 2ln\left( {{e^{\frac{1}{2}}}.{x^{\frac{1}{2}}}} \right) - \left( {ln{e^2} - ln{x^{\frac{1}{2}}}} \right) + ln3.\frac{{ln(e.{x^2})}}{{ln3}}\]
\[ = 2(\frac{1}{2} + \frac{1}{2}lnx) - (2 - \frac{1}{2}lnx) + lne + 2lnx\]
\[ = 2(\frac{1}{2} + \frac{1}{2}.2) - (2 - \frac{1}{2}.2) + 1 + 2.2 = 7\]
Đáp án cần chọn là: A
