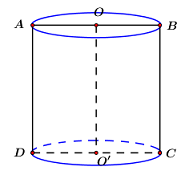
Diện tích hình trụ, thể tích khối trụ
-
397 lượt thi
-
40 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trục đường tròn là đường thẳng đi qua tâm và:
 Xem đáp án
Xem đáp án
- Trục của đường tròn: là đường thẳng vuông góc với mặt phẳng chứa đường tròn tại tâm của nó.
Đáp án cần chọn là: C
Câu 2:
Cho hai đường thẳng d và \[\Delta \], điều kiện nào sau đây của d và \[\Delta \] thì khi quay d quanh \[\Delta \] ta được một mặt trụ?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 3:
Khi quay hình chữ nhật ABCD quanh các cạnh nào dưới đây ta được hai hình trụ có cùng chiều cao?
 Xem đáp án
Xem đáp án
- Quay hình chữ nhật quanh một cạnh thì ta được hình trụ nên loại đáp án C và B vì có các đường chéo.
- Do AB ≠ AD nên hai hình trụ tạo thành có chiều cao khác nhau.
- Do AD = BC nên hai hình trụ tạo thành có chiều cao bằng nhau.
Đáp án cần chọn là: D
Câu 4:
Cho hình chữ nhật ABCD, khi quay hình chữ nhật quanh cạnh AD thì CD được gọi là:
 Xem đáp án
Xem đáp án
Quay hình chữ nhật ABCD quanh cạnh AD thì được hình trụ có chiều cao AD, đường sinh BC và bán kính đáy AB,CD.
Do đó CD được gọi là bán kính đáy.
Đáp án cần chọn là: D
Câu 5:
Khi quay hình chữ nhật MNPQ quanh đường thẳng AB với A,B lần lượt là trung điểm của MN,PQ ta được một hình trụ có đường kính đáy:
 Xem đáp án
Xem đáp án
Hình trụ tạo thành khi quay hình chữ nhật MNPQ quanh đường trung bình AB ta sẽ được hình trụ có đường cao AB, đường sinh MQ,NP và bán kính đáy MA,NA,BP,BQ đường kính đáy MN,PQ.
Do đó đường kính đáy của hình trụ là MN.
Đáp án cần chọn là: D
Câu 6:
Nếu cắt mặt trụ bởi mặt phẳng vuông góc với trục ta được là:
 Xem đáp án
Xem đáp án
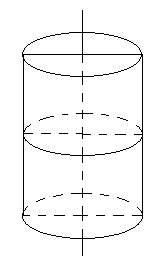
Khi cắt mặt trụ bởi mặt phẳng vuông góc với đáy ta được đường tròn có bán kính bằng bán kính mặt trụ.
Đáp án cần chọn là: B
Câu 7:
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \[\alpha ({0^0} < \alpha < {90^0})\;\] thì ta được:
 Xem đáp án
Xem đáp án
Khi cắt mặt trụ bởi mặt phẳng tạo với trục một góc \[\alpha ({0^0} < \alpha < {90^0})\] thì ta được elip.
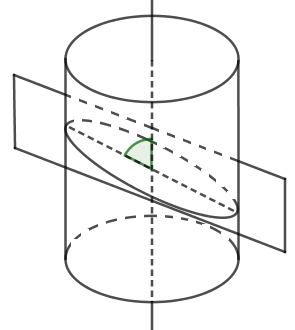
Đáp án cần chọn là: D
</>
Câu 8:
Cho hình trụ có trục \[\Delta \] và bán kính R. Khi cắt hình trụ bởi mặt phẳng \[(\alpha )\;\]song song với \[\Delta \] và cách \[\Delta \] một khoảng \[d(\Delta ;(\alpha )) = k < R\;\] thì ta được thiết diện là:
 Xem đáp án
Xem đáp án
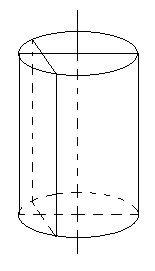
Khi cắt hình trụ bởi mặt phẳng song song với trục mà khoảng cách giữa \[\left( \alpha \right)\]và trục nhỏ hơn bán kính hình trụ thì ta được thiết diện là hình chữ nhật.
Đáp án cần chọn là: A
Câu 9. Công thức tính diện tích xung quanh hình trụ có bán kính đáy r và chiều cao h là:
A.\[{S_{xq}} = \pi {r^2}h\]
B. \[{S_{xq}} = \pi rh\]
C. \[{S_{xq}} = 2\pi rh\]
D. \[{S_{xq}} = \frac{1}{3}\pi {r^2}h\]
Công thức tính diện tích xung quanh hình trụ: \[{S_{xq}} = 2\pi rh\]
Đáp án cần chọn là: C
Câu 9:
Hình trụ có bán kính đáy r = 2cm và chiều cao h = 5cm có diện tích xung quanh:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 10:
Công thức tính diện tích toàn phần hình trụ có bán kính r và chiều cao h là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 11:
Công thức nào sau đây không đúng khi tính diện tích toàn phần hình trụ?
 Xem đáp án
Xem đáp án
Ta có: \[{S_{tp}} = {S_{xq}} + 2{S_d} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right) = {C_d}.\left( {h + r} \right)\]
Dó đó công thức ở đáp án D là sai.
Đáp án cần chọn là: D
Câu 12:
Hình trụ có bán kính r = 5cm và chiều cao h = 3cm có diện tích toàn phần gần với số nào sau đây?
 Xem đáp án
Xem đáp án
Ta có: \[{S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi .5.3 + 2\pi {.5^2} \approx 251,3c{m^2}\]
Đáp án cần chọn là: A
Câu 13:
Công thức tính thể tích khối trụ có bán kính r và chiều cao h là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 14:
Thể tích khối trụ có bán kính r = 4cm và chiều cao h = 5cm là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 15:
Cho hình chữ nhật ABCD có AB = 3, BC = 4. Gọi V1,V2 lần lượt là thể tích của các khối trụ sinh ra khi quay hình chữ nhật quanh trục AB và BC. Khi đó tỉ số\(\frac{{{V_2}}}{{{V_2}}}\) bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 16:
Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng V và diện tích toàn phần phần hình trụ nhỏ nhất thì bán kính đáy R bằng:
 Xem đáp án
Xem đáp án
Hình trụ đó có chiều cao \[h = \frac{V}{{\pi {R^2}}}\] và diện tích toàn phần
\[{S_{tp}} = 2\pi {R^2} + 2\pi Rh = 2\pi {R^2} + \frac{{2V}}{R} = 2\pi {R^2} + \frac{V}{R} + \frac{V}{R} \ge 3\sqrt[3]{{2\pi {R^2}.\frac{V}{R}.\frac{V}{R}}} = 3\sqrt[3]{{2\pi {V^2}}}\]
Dấu “=” xảy ra \[ \Leftrightarrow 2\pi {R^2} = \frac{V}{R} \Leftrightarrow {R^3} = \frac{V}{{2\pi }} \Leftrightarrow R = \sqrt[3]{{\frac{V}{{2\pi }}}}\]
Đáp án cần chọn là: A
Câu 17:
Từ một tấm tôn hình chữ nhật kích thước 50cm×240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V1 là thể tích của thùng gò được theo cách 1 và V2 là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)
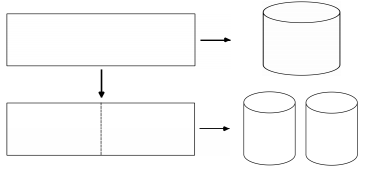
 Xem đáp án
Xem đáp án
Cách 1: Chu vi đáy là\[240cm \Rightarrow 2\pi {R_1} = 240 \Leftrightarrow {R_1} = \frac{{120}}{\pi }\]
\[ \Rightarrow {V_1} = \pi R_1^2h = \pi {\left( {\frac{{120}}{\pi }} \right)^2}h = \frac{{{{120}^2}.50}}{\pi }\]
Cách 2: Chu vi đáy mỗi hình trụ nhỏ là:
\[240:2 = 120cm \Rightarrow 2\pi R = 120 \Rightarrow R = \frac{{60}}{\pi }\]
\[ \Rightarrow V = \pi {R^2}h = \pi {\left( {\frac{{60}}{\pi }} \right)^2}.50 = \frac{{{{60}^2}.50}}{\pi } \Rightarrow {V_2} = 2V = \frac{{{{2.60}^2}.50}}{\pi }\]
Vậy \[\frac{{{V_1}}}{{{V_2}}} = \frac{{{{120}^2}.50}}{\pi }:\frac{{{{2.60}^2}.50}}{\pi } = 2\]
Một đường tròn có bán kính rr thì có chu vi và diện tích lần lượt là
\[C = 2\pi r;S = \pi {r^2} \Rightarrow S = \frac{{{C^2}}}{{4\pi }}\]
Gọi chiều dài tấm tôn là a thì tổng diện tích đáy của thùng theo 2 cách lần lượt là
\[{S_1} = \frac{{{a^2}}}{{4\pi }};{S_2} = 2.\frac{{{{\left( {\frac{a}{2}} \right)}^2}}}{{4\pi }} = \frac{{{a^2}}}{{8\pi }} \Rightarrow \frac{{{S_1}}}{{{S_2}}} = 2 \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 2\]
Đáp án cần chọn là: C
Câu 18:
Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 19:
Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2m,3m,2m lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo nước hình trụ có chiều cao là 5cm và bán kính đường tròn đáy là 4cm. Trung bình một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau bao nhiêu ngày thì bể hết nước biết rằng ban đầu bể đầy nước?
 Xem đáp án
Xem đáp án
Thể tích gáo \[{V_1} = \pi {R^2}.h = \pi .0,{04^2}.0,05 = 8\pi {.10^{ - 5}}({m^3})\]
Số nước múc ra trong một ngày \[{V_2} = 170{V_1} = 170.8.\pi {.10^{ - 5}} = 0,0136\pi \left( {{m^3}} \right)\]
Số ngày dùng hết nước là \[\frac{{2.3.2}}{{{V_2}}} = \frac{{12}}{{0,0136\pi }} \approx 281\] (ngày)
Đáp án cần chọn là: B
Câu 20:
Một cái cốc hình trụ cao 15cm đựng được 0,5 lít nước. Hỏi bán kính đường tròn đáy đáy của cốc xấp xỉ bằng bao nhiêu (làm tròn đến hàng thập phân thứ hai)?
 Xem đáp án
Xem đáp án
\[V = Sh = \pi {R^2}.h \Rightarrow R = \sqrt {\frac{V}{{\pi h}}} = \sqrt {\frac{{0,{{5.10}^{ - 3}}}}{{\pi .0,15}}} = 0,0326(m) = 3,26(cm)\]
Đáp án cần chọn là: A
Câu 21:
Một đội xây dựng cần hoàn thiện một hệ thống cột tròn của một cửa hàng kinh doanh gồm 17 chiếc. Trước khi hoàn thiện mỗi chiếc cột là một khối bê tông cốt thép hình lăng trụ lục giác đều có cạnh 14cm; sau khi hoàn thiện (bằng cách trát thêm vữa tổng hợp vào xung quanh) mỗi cột là một khối trụ có đường kính đáy bằng30cm. Biết chiều cao của mỗi cột trước và sau khi hoàn thiện là 390cm. Tỉnh lượng vữa hỗn hợp cần dùng (tính theo đơn vị m3, làm tròn đến 1 chữ số thập phân sau dấu phầy). Ta có kết quả:
 Xem đáp án
Xem đáp án
- Với cột bê tông hình lăng trụ:
Đáy của mỗi cột là hình lục giác đều có diện tích bằng 6 tam giác đều cạnh 14cm, mỗi tam giác có diện tích là\[\frac{{{{14}^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\]
- Với cột bê tông đã trát vữa hình trụ:
Đáy của mỗi cột là hình tròn bán kính 15cm nên có diện tích là \[{15^2}\pi \left( {c{m^2}} \right)\]
Số lượng vữa cần trát thêm vào tất cả 17 cột, mỗi cột cao 390cm là:
\[17.390\left( {{{15}^2}\pi - 6.\frac{{{{14}^2}\sqrt 3 }}{4}} \right) = 1,{31.10^6}c{m^3} = 1,31{m^3}\]
Đáp án cần chọn là: A
Câu 22:
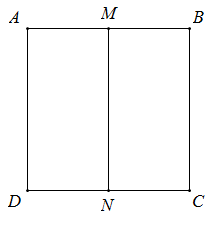
Cho hình vuông ABCD có cạnh bằng aa. Gọi M,N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN tạo thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu (S) là:
 Xem đáp án
Xem đáp án
Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có chiều cao h = a và bán kính đáy\[r = \frac{a}{2}\]nên có diện tích toàn phần:
\[{S_{tp}} = 2\pi r\left( {r + h} \right) = 2\pi .\frac{a}{2}\left( {\frac{a}{2} + a} \right) = \frac{{3{a^2}\pi }}{2}\]
Mặt cầu (S) có diện tích bằng Stp của mặt trụ thì có bán kính R với:
\[4\pi {R^2} = \frac{{3{a^2}\pi }}{2} \Leftrightarrow R = \frac{{a\sqrt 6 }}{4}\]
Đáp án cần chọn là: C
Câu 23:
Một hình trụ có chiều cao bằng 3, chu vi đáy bằng \[4\pi \]. Thể tích của khối trụ là:
 Xem đáp án
Xem đáp án
Bán kính đáy: \[r = \frac{C}{{2\pi }} = \frac{{4\pi }}{{2\pi }} = 2\]
Thể tích của khối trụ: \[V = \pi {r^2}h = \pi {.2^2}.3 = 12\pi \]
Đáp án cần chọn là: D
Câu 24:
Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a.
 Xem đáp án
Xem đáp án
Khối trụ ngoại tiếp hình lập phương có cạnh bằng a thì bán kính đáy \[r = \frac{{a\sqrt 2 }}{2}\]và chiều cao h = a
Suy ra\[V = \pi {r^2}h = \frac{{\pi {a^3}}}{2}\]
Đáp án cần chọn là: D
Câu 25:
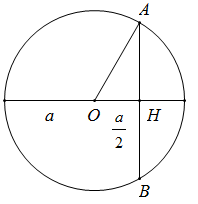
Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\frac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.
 Xem đáp án
Xem đáp án
Gọi (O) là một đường tròn đáy của hình trụ
Mặt phẳng đã cho cắt (O) tại A và B, gọi H là trung điểm AB.
Vì thiết diện thu được là hình vuông nên chiều cao hình trụ bằng
\[h = AB = 2AH = 2\sqrt {O{A^2} - O{H^2}} = a\sqrt 3 \]
Thể tích khối trụ là
\[V = \pi {R^2}h = \pi {a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 \]
Đáp án cần chọn là: A
Câu 26:
Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông cạnh a. Tính diện tích toàn phần S của hình trụ.
 Xem đáp án
Xem đáp án
Ta có: \[r = OA = \frac{{AB}}{2} = \frac{a}{2};h = AA' = a\]nên
\[{S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi .\frac{a}{2}.a + 2\pi .{\left( {\frac{a}{2}} \right)^2} = \pi {a^2} + \frac{{\pi {a^2}}}{2} = \frac{{3\pi {a^2}}}{2}\]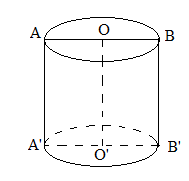
Đáp án cần chọn là: A
Câu 27:
Cho hình trụ có các đáy là hình tròn tâm O và tâm O′ , bán kính đáy bằng chiều cao và bằng 4cm. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O′ lấy điểm B sao cho \[AB = 4\sqrt 3 cm\]. Thể tích khối tứ diện AOO′B là:
 Xem đáp án
Xem đáp án
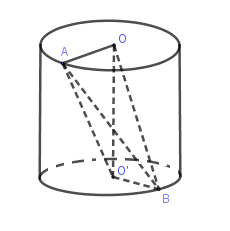
Tam giác OAO′ vuông tại O nên:
\[O'A = \sqrt {O{A^2} + O'{O^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \]
Tam giác AO′B có:
\[O'{A^2} + O'{B^2} = A{B^2}\] nên tam giác AO′B vuông tại O′
Ta có \(\left\{ {\begin{array}{*{20}{c}}{O\prime B \bot OO\prime }\\{O\prime B \bot AO\prime }\end{array}} \right. \Rightarrow O\prime B \bot (AOO\prime )\)\[{S_{{\rm{\Delta }}AOO'}} = \frac{1}{2}OA.OO = \frac{1}{2}.4.4 = 8\]
\[ \Rightarrow {V_{AOO'B}} = \frac{1}{3}{S_{{\rm{\Delta }}AOO'}}.O'B = \frac{1}{3}.8.4 = \frac{{32}}{3}\]
Đáp án cần chọn là: A
Câu 28:
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là r1,h1,r2,h2 thỏa mãn \[{r_2} = \frac{1}{2}{r_1},{h_2} = 2{h_1}\] (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 30cm3 . Tính thể tích khối trụ (H1) bằng:
 Xem đáp án
Xem đáp án
Thể tích của toàn bộ khối đồ chơi là:
\[\begin{array}{*{20}{l}}{V = \pi r_1^2{h_1} + \pi r_2^2{h_2} = \pi r_1^2{h_1} + \pi \frac{1}{4}r_1^2.2{h_1} = \frac{3}{2}\pi r_1^2{h_1} = 30}\\{ \Rightarrow \pi r_1^2{h_1} = 20}\end{array}\]
Vậy thể tích khối trụ (H1) là 20 cm3.
Đáp án cần chọn là: C
Câu 29:
Người ta xếp hai quả cầu có cùng bán kính r vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảo hình vẽ). Biết thể tích khối trụ là 120cm3, thể tích của mỗi khối cầu bằng
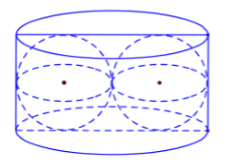
 Xem đáp án
Xem đáp án
Dựa vào dữ kiện bài toán và hình vẽ ⇒ Hình trụ có chiều cao h = 2r và bán kính đáy R = 2r .
⇒ Thể tích khối trụ là\[V = \pi {\left( {2r} \right)^2}2r = 8\pi {r^3} = 120 \Leftrightarrow {r^3} = \frac{{120}}{{8\pi }} = \frac{{15}}{\pi }\]
Vậy thể tích mỗi khối cầu là \[{V_c} = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi .\frac{{15}}{\pi } = 20\,\,\left( {c{m^3}} \right)\]
Đáp án cần chọn là: B
Câu 30:
Cho hình trụ bán kính đường tròn đáy bằng 1. Hai điểm A và B lần lượt thuộc hai đường tròn đáy sao cho \[AB = \sqrt 6 \], khoảng cách giữa hai đường thẳng AB và trục của hình trụ bằng 12. Thể tích khối trụ được giới hạn bởi hình trụ đó bằng:
 Xem đáp án
Xem đáp án
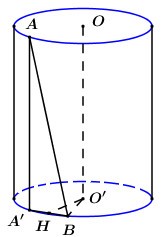
Gọi O,O′ lần lượt là tâm đường tròn đáy chứa A,B.
Gọi A′ là hình chiếu của A lên đường tròn đáy chứa điểm B.
Ta có\[AA'\parallel OO' \Rightarrow OO'\parallel \left( {AA'B} \right) \supset AB\]
\[ \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'B} \right)} \right) = d\left( {O';\left( {AA'B} \right)} \right)\]
Gọi H là trung điểm của A′B, ta có \[O'H \bot A'B\] (quan hệ vuông góc giữa đường kính và dây cung).
Khi đó ta có:\(\left\{ {\begin{array}{*{20}{c}}{O\prime H \bot A\prime B}\\{O\prime H \bot AA\prime }\end{array}} \right. \Rightarrow O\prime H \bot (AA\prime B) \Rightarrow d\left( {OO';AB} \right) = OH = \frac{1}{2}\)
Áp dụng định lí Pytago trong tam giác vuông O′HB có
\[HB = \sqrt {O'{B^2} - O'{H^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\]
\[ \Rightarrow A'B = 2HB = \sqrt 3 \]
Áp dụng định lí Pytago trong tam giác vuông có:
\[AA' = \sqrt {A{B^2} - A'{B^2}} = \sqrt {6 - 3} = \sqrt 3 \]
Vậy thể tích khối trụ là \[V = \pi {r^2}h = \pi {.1^2}.\sqrt 3 = \pi \sqrt 3 \]Đáp án cần chọn là: C
Câu 31:
Trong không gian Oxyz, tập hợp các điểm M(a;b;c) sao cho \[{a^2} + {b^2} \le 2,\,\,\left| c \right| \le 8\] là một khối tròn xoay. Tính thể tích của khối tròn xoay đó?
 Xem đáp án
Xem đáp án
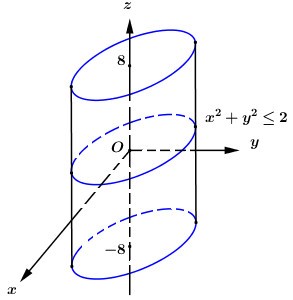
Tập hợp các điểm M(a;b;c) sao cho\[{a^2} + {b^2} \le 2,\,\,\left| c \right| \le 8\] là khối trụ có bán kính đáy \[r = \sqrt 2 \] chiều cao h = 16 .
Do đó thể tích khối trụ là \[V = \pi {r^2}h = \pi .{\left( {\sqrt 2 } \right)^2}.16 = 32\pi \]
Đáp án cần chọn là: C
Câu 32:
Một hình trụ có diện tích xung quanh là \[16\pi \], thiết diện qua trục là hình vuông. Một mặt phẳng \[(\alpha )\;\]song song với trục, cắt hình trụ theo thiết diện là ABB′A′, biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 1200. Chu vi tứ giác ABB′A′ bằng:
 Xem đáp án
Xem đáp án
Gọi r,h lần lượt là bán kính đáy và chiều cao của hình trụ, ta có
\[{S_{xq}} = 2\pi rh \Leftrightarrow 16\pi = 2\pi rh \Leftrightarrow rh = 8\]
Lại có thiết diện qua trục là hình vuông nên \[h = 2r\]do đó \[r.2r = 8 \Leftrightarrow {r^2} = 4\]
\[ \Rightarrow r = 2,\,\,h = 4 = AA'\]
Theo bài ra ta có: \[\angle AOB = {120^0}\]Áp dụng định lí Cosin trong tam giác OAB ta có:
\[\begin{array}{*{20}{l}}{A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB}\\{A{B^2} = {r^2} + {r^2} - 2.r.r.\cos {{120}^0}}\\{A{B^2} = 3{r^2}}\\{ \Rightarrow AB = r\sqrt 3 = 2.\sqrt 3 }\end{array}\]
Vậy \[{C_{ABB'A'}} = 2\left( {AB + AA'} \right) = 2\left( {2\sqrt 3 + 4} \right) = 8 + 4\sqrt 3 \]Đáp án cần chọn là: D
Câu 33:
Cho hình trụ có bán kính đáy bằng 1 và chiều cao bằng 3. Thiết diện của hình trụ cắt bởi mặt phẳng qua trục của nó có diện tích bằng:
 Xem đáp án
Xem đáp án
Giả sử thiết diện qua trục là hình chữ nhật ABCD, ta có \[AD = h = 3,\,\,AB = 2r = 2\]Vậy \[{S_{ABCD}} = 3.2 = 6\]Đáp án cần chọn là: D
Câu 34:
Cho khối trụ có hai đáy là (O) và (O′). AB,CD lần lượt là hai đường kính của (O) và (O′), góc giữa AB và CD bằng 300, AB = 6 và thể tích khối tứ diện ABCD bằng 30. Thể tích khối trụ đã cho bằng:
 Xem đáp án
Xem đáp án
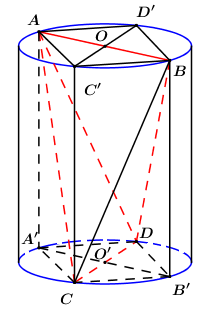
Gọi A′,B′ lần lượt là hình chiếu của A,B lên đường tròn (O).
C′,D′ lần lượt là hình chiếu của C,D lên đường tròn (O′).
=>AC′BD′ là hình bình hành, lại có AB = CD = C′D′ nên AC′BD′ là hình chữ nhật.
Khi đó AC′BD′.A′CB′D là hình hộp chữ nhật.
Ta có:\[{V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + {V_{A.A'CD}} + {V_{B.B'CD}} + {V_{C.C'AB}} + {V_{D.D'AB}}\]
Ta có:\[{V_{A.A'CD}} = \frac{1}{3}AA'.{S_{A'CD}} = \frac{1}{3}AA'.\frac{1}{2}{S_{A'CB'D}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\]
CMTT ta có: \[{V_{B.B'CD}} = {V_{C.C'AB}} = {V_{D.D'AB}} = \frac{1}{6}{V_{AC'BD'.A'CB'D}}\]
\[\begin{array}{*{20}{l}}{ \Rightarrow {V_{AC'BD'.A'CB'D}} = {V_{ABCD}} + 4.\frac{1}{6}{V_{AC'BD'.A'CB'D}}}\\{ \Rightarrow {V_{ABCD}} = \frac{1}{3}{V_{AC'BD'.A'CB'D}} = 30}\\{ \Rightarrow {V_{AC'BD'.A'CB'D}} = 90}\end{array}\]
Theo bài ra ta có: \[\angle \left( {AB;CD} \right) = {30^0} \Rightarrow \angle \left( {AB;C'D'} \right) = {30^0}\]giả sử\[\angle \left( {AB;C'D'} \right) = \angle \[ \Rightarrow {S_{AC'BD'}} = 4{S_{OAC'}} = 9\]Lại có \[OA = OC' = \frac{1}{2}AB = 3\]
\[ \Rightarrow {S_{OAC'}} = \frac{1}{2}OA.OC'.\sin \angle AOC' = \frac{1}{2}.3.3.\sin {30^0} = \frac{9}{4}\]
Ta có: \[{V_{AC'BD'.A'CB'D}} = AA'.{S_{AC'BD'}} \Rightarrow 90 = AA'.9 \Leftrightarrow AA' = 10\]
Vậy thể tích khối trụ là \[V = \pi {r^2}h = \pi .O{A^2}.AA' = \pi {.3^2}.10 = 90\pi \]
Đáp án cần chọn là: B
Câu 35:
Thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 10. Diện tích xung quanh của hình trụ đó bằng:
 Xem đáp án
Xem đáp án
Ta có: \[{S_{ABCD}} = AB.AD = 2rh = 10.\]
\[ \Rightarrow {S_{xq}} = 2\pi rh = 10\pi .\]Đáp án cần chọn là: A
Câu 36:
Một cái nồi có dạng hình trụ có chiều cao 60cm và diện tích đáy là \[900\pi c{m^2}\]. Hỏi cần miếng kim loại hình chữ nhật có kích thước bao nhiêu để làm thân nồi?
 Xem đáp án
Xem đáp án
Ta có hình trụ có diện tích đáy là \[S = \pi {R^2} = 900\pi \Leftrightarrow R = 30cm\].
Diện tích xung quanh hình trụ là \[S = 2\pi Rh = 2\pi .30.60 = 60\pi .60(c{m^2}).\]
Vậy cần miếng kim loại hình chữ nhật chiều dài \[60\pi cm\] và chiều rộng 60cm
Đáp án cần chọn là: B
Câu 37:
Một sợi dây (không co giãn) được quấn đối xứng đúng 10 vòng quanh một ống trụ tròn đều có bán kính \(R = \frac{2}{\pi }cm\) (như hình vẽ).
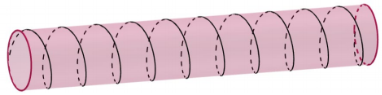
Biết rằng sợi dây có chiều dài 50 cm. Hãy tính diện tích xung quanh của ống trụ đó.
D.120 cm2
 Xem đáp án
Xem đáp án
Gọi độ dài đường cao của ống trụ là 10x(cm)(x > 0)
Chia ống trụ thành 10 phần bằng nhau, mỗi phần có độ dài đường sinh là x(cm).
Trải phẳng mỗi ống trụ nhỏ ta được 1 hình chữ nhật có hai kích thước là x và \[2\pi .R = 2\pi .\frac{2}{\pi } = 4\,\,\left( {cm} \right)\]
Khi đó độ dài đường chéo của hình chữ nhật là \[\sqrt {{x^2} + {4^2}} = \sqrt {{x^2} + 16} \], và độ dài đường chéo chính bằng độ dài của 1 vòng.
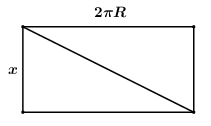
Do đó ta có phương trình: \[10\sqrt {{x^2} + 16} = 50 \Leftrightarrow \sqrt {{x^2} + 16} = 5\]
\[ \Rightarrow {x^2} + 16 = 25 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = 3\,\,\left( {cm} \right)\,\,\left( {tm} \right)\]Độ dài đường cao của ống trụ là \[h = 10x = 30(cm)\]
Vậy diện tích xung quanh của ống trụ là \[{S_{xq}} = 2\pi Rh = 2\pi .\frac{2}{\pi }.30 = 120\,\,\left( {c{m^2}} \right)\].
Đáp án cần chọn là: D
Câu 38:
Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ (T) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của (T) bằng:
 Xem đáp án
Xem đáp án
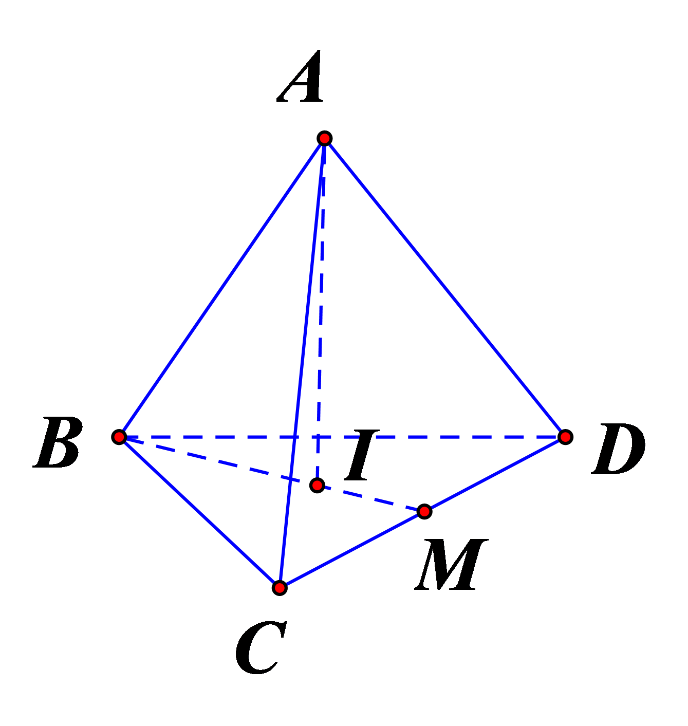
Tam giác BCD là tam giác đều cạnh 4\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{SBCD = 4\sqrt 3 }\\{p = 12}\end{array}} \right.\)
Áp dụng công thức tính bán kính đường tròn nội tiếp ta có:\[R = \frac{{2S}}{p} = \frac{{2\sqrt 3 }}{3}\]
Gọi O là tâm của tam giác đều BCD \[ \Rightarrow AO \bot \left( {BCD} \right) \Rightarrow {\rm{\Delta }}ABO\] vuông tại O có
\[BO = \frac{{4\sqrt 3 }}{3};AB = 4 \Rightarrow AO = h = \frac{{4\sqrt 6 }}{3}\]
Khi đó diện tích xung quanh hình trụ có \[h = \frac{{4\sqrt 6 }}{3};R = \frac{{2\sqrt 3 }}{3}\] là \[S = 2\pi Rh = \frac{{16\sqrt 2 \pi }}{3}\]Đáp án cần chọn là: A
Câu 39:
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng 12. Giá trị lớn nhất của thể tích khối trụ bằng
 Xem đáp án
Xem đáp án
Gọi R,h lần lượt là bán kính đáy và chiều cao của hình trụ.
Giả sử thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật ABCD như hình vẽ, ta có AB = 2R và AD = h.
Chu vi thiết diện chứa trục bằng 12 \[ \Rightarrow 2R + h = 6 \Rightarrow h = 6 - 2R\]
Khi đó thể tích khối trụ:
\[V = \pi {R^2}h = \pi {R^2}\left( {6 - 2R} \right) = \pi .R.R\left( {6 - 2R} \right) \le \pi .{\left( {\frac{{R + R + 6 - 2R}}{3}} \right)^3} = 8\pi \]
Dấu “=” xảy ra khi và chỉ khi \[R = 6 - 2R \Leftrightarrow R = 2.\]
Vậy thể tích khối trụ lớn nhất là \[8\pi \] khi R = 2.
Đáp án cần chọn là: C
Câu 40:
Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5cm. Mặt phẳng \[(\alpha )\;\]song song với trục, cắt hình trụ theo một thiết diện có chu vi bằng 26cm. Khoảng cách từ \[(\alpha )\;\]đến trục của hình trụ bằng:
 Xem đáp án
Xem đáp án
Mặt phẳng \[(\alpha )\;\]song song với trục, cắt hình trụ theo thiết diện là một hình chữ nhật ABCD với AD = BC = h = 5.
\[ \Rightarrow 2\left( {AB + BC} \right) = 2\left( {AB + 5} \right) = 26 \Leftrightarrow AB = 8\,\,cm.\]
Gọi H là trung điểm của \[AB \Rightarrow OH \bot AB \Rightarrow OH \bot \left( {ABCD} \right)\]hay \[OH \bot \left( \alpha \right).\]
\[ \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = d\left( {O;\,\,\left( \alpha \right)} \right) = OH.\]
\[ \Rightarrow AH = \frac{{AB}}{2} = 4\,\,cm.\]
Áp dụng định lý Pitago cho \[{\rm{\Delta }}AOH\] vuông tại HH ta có:\[\begin{array}{*{20}{l}}{OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = 3cm.}\\{ \Rightarrow d\left( {OO';\,\,\left( \alpha \right)} \right) = 3\,cm.}\end{array}\]
Đáp án cần chọn là: D
