Góc giữa đường thẳng và mặt phẳng
-
634 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tứ diện ABCD có cạnh AB, BC, CD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Từ giả thiết ta có\(\left\{ {\begin{array}{*{20}{c}}{AB \bot BC}\\{AB \bot CD}\end{array}} \right. \Rightarrow AB \bot (BCD)\)
Do đó\[\left( {AC,\left( {BCD} \right)} \right) = \left( {AC,BC} \right) = \widehat {ACB}\]
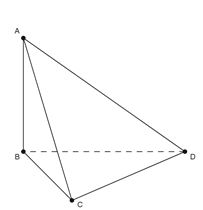
Đáp án cần chọn là: A
Câu 2:
Cho tam giác ABC vuông cân tại A và BC=a.. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm SS sao cho \(SA = \frac{{a\sqrt 6 }}{2}\). Tính số đo góc giữa đường thẳng SA và (ABC)
 Xem đáp án
Xem đáp án
\[SA \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = {90^ \circ }\]
Đáp án cần chọn là: D
Câu 3:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC=a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB=a. Tính số đo của góc giữa SA và (ABC).
 Xem đáp án
Xem đáp án
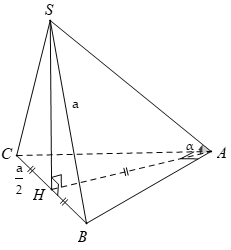
Gọi H là trung điểm của BC suy ra
\[AH = BH = CH = \frac{1}{2}BC = \frac{a}{2}\]
Ta có:\[SH \bot \left( {ABC} \right) \Rightarrow SH = \sqrt {S{B^2} - B{H^2}} = \frac{{a\sqrt 3 }}{2}\]
\[\widehat {\left( {SA,\left( {ABC} \right)} \right)} = \widehat {\left( {SA,HA} \right)} = \widehat {SAH} = \alpha \]
\[ \Rightarrow \tan \alpha = \frac{{SH}}{{AH}} = \sqrt 3 \Rightarrow \alpha = {60^ \circ }\]
Đáp án cần chọn là: C
Câu 4:
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng aa và \[SA \bot (ABCD)\] Biết \(SA = \frac{{a\sqrt 6 }}{3}\). Tính góc giữa SC và (ABCD).
 Xem đáp án
Xem đáp án
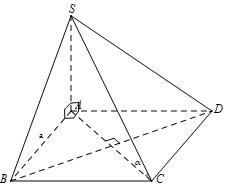
Ta có: \[SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC\]
\[ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA} = \alpha \]
ABCD là hình vuông cạnh\[a \Rightarrow AC = a\sqrt 2 ,SA = \frac{{a\sqrt 6 }}{3}\]
\[ \Rightarrow \tan \alpha = \frac{{SA}}{{AC}} = \frac{{\sqrt 3 }}{3} \Rightarrow \alpha = {30^ \circ }\]
Đáp án cần chọn là: A
Câu 5:
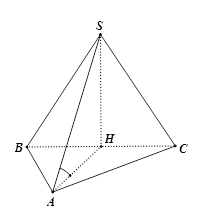
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
 Xem đáp án
Xem đáp án
Do H là hình chiếu của S lên mặt phẳng (ABC) nên \[SH \bot (ABC)\]
Vậy AH là hình chiếu của SA lên mp (ABC)
\[ \Rightarrow \left( {SA;\left( {ABC} \right)} \right) = \left( {SA;HA} \right) = \widehat {SAH}\] (do\[SH \bot \left( {ABC} \right) \Rightarrow SH \bot AH\]hay \[\widehat {SAH} < {90^0}\]Mà: \[{\rm{\Delta }}ABC = {\rm{\Delta }}SBC \Rightarrow SH = AH\]
Vậy tam giác SAH vuông cân tại H ⇒\[\widehat {SAH} = {45^0}\]
Đáp án cần chọn là: C
Câu 6:
Cho hình lập phương ABCD.A′B′C′D′. Gọi \[\alpha \] là góc giữa AC′ và mp .(A′BCD′). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
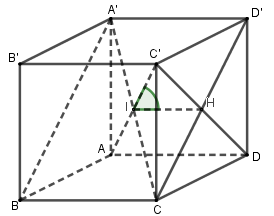
Gọi \(\left\{ {\begin{array}{*{20}{c}}{A\prime C \cap AC\prime = I}\\{C\prime D \cap CD\prime = H}\end{array}} \right.\)
mà\(\left\{ {\begin{array}{*{20}{c}}{C\prime D \bot CD\prime }\\{C\prime D \bot A\prime D'}\end{array}} \right. \Rightarrow C\prime D \bot (A\prime BCD\prime ) \Rightarrow IH\) là hình chiếu vuông góc của IC′ lên\[\left( {A'BCD'} \right) \Rightarrow \widehat {C'IH}\] là góc giữa\[IC'\] và \[\left( {A'BCD'} \right)\] và cũng là góc giữa AC′ và\[\left( {A'BCD'} \right).\] Mà\[\tan \widehat {C'IH} = \frac{{C'H}}{{IH}} = \frac{1}{{\sqrt 2 }}.2 = \sqrt 2 .\]
Đáp án cần chọn là: D
Câu 7:
Trong các mệnh đề sau mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án A sai vì nếu trường hợp đường thẳng vuông góc với mặt phẳng thì định nghĩa đó không còn đúng.
Đáp án C sai vì (P) và (Q) có thể trùng nhau.
Đáp án D sai vì a,b có thể trùng nhau.
Đáp án cần chọn là: B
Câu 8:
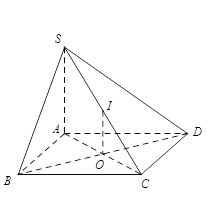
Cho hình chóp S.ABCD có \[SA \bot (ABCD)\] và đáy ABCD là hình chữ nhật. Gọi O là tâm của ABCD và I là trung điểm của SC. Khẳng định nào sau đây sai ?
 Xem đáp án
Xem đáp án
Có IO là đường trung bình tam giác SAC nên \[IO//SA\;\] nên \[IO \bot (ABCD)\;\] nên A đúng.
Có \(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot SB\) nên B đúng
Và \(\left\{ {\begin{array}{*{20}{c}}{CD \bot AD}\\{CD \bot SA}\end{array}} \right. \Rightarrow CD \bot SD\) nên phương án D đúng.
Đáp án C sai vì nếu (SAC) là mặt phẳng trung trực của \[BD \Rightarrow BD \bot AC\] (vô lý).
Đáp án cần chọn là: C
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \[SA \bot (ABCD),\;SA = a\sqrt 6 \]. Gọi \[\alpha \] là góc giữa SC và mp(SAB). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
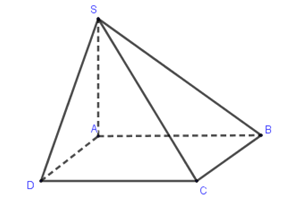
Bước 1:
Do \[BC \bot \left( {SAB} \right)\]⇒ B là hình chiếu của C lên (SAB)
Mà S là hình chiếu của chính nó lên (SAB).
⇒SB là hình chiếu của SC lên (SAB)
⇒ Góc giữa SC và (SAB) là góc giữa SC và SB và bằng \[\widehat {BSC}\]
Bước 2:
Ta có:
\[SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {6{a^2} + {a^2}} = a\sqrt 7 \]
Xét tam giác SBC có
\[\tan \widehat {BSC} = \frac{{BC}}{{SB}} = \frac{a}{{a\sqrt 7 }} = \frac{1}{{\sqrt 7 }}.\]
Đáp án cần chọn là: B
Câu 10:
Cho hình chóp S.ABCD, với đáy ABCD là hình bình hành tâm O;AD,SA,AB đôi một vuông góc AD=8,SA=6. (P)là mặt phẳng qua trung điểm của AB và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng?
 Xem đáp án
Xem đáp án
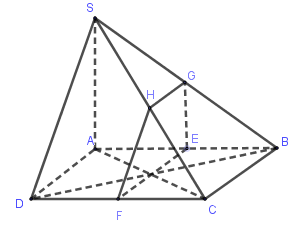
Gọi E là trung điểm của AB.
Qua E kẻ\[EF \bot CD,EG \bot AB \Rightarrow \left( {EGF} \right) \bot AB\] và F,G là trung điểm của DC,SB.
Do\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABCD) = BC}\\{(EGF) \cap (ABCD) = FE}\\{FE//BC}\end{array}} \right. \Rightarrow \left( {SBC} \right) \cap \left( {EGF} \right) = GH//BC\) (định lý giao tuyến ba mặt phẳng)
Suy ra H là trung điểm của SC.
Vậy thiết diện là hình thang GHFE.
Vì \[GE//SA\] nên \[GE \bot \left( {ABCD} \right) \Rightarrow GE \bot FE\] nên thiết diện là hình thang vuông.
\[{S_{EGHF}} = \frac{{\left( {FE + GH} \right).GE}}{2} = \frac{{\left( {BC + \frac{1}{2}BC} \right).\frac{1}{2}SA}}{2} = \frac{{\left( {8 + 4} \right)3}}{2} = 18\]
Đáp án cần chọn là: D
Câu 11:
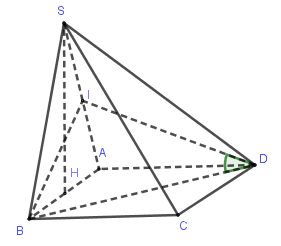
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm \[\Delta ABC\]. Độ dài SG là:
 Xem đáp án
Xem đáp án
Theo bài ra hình chóp S.ABC là hình chóp tam giác đều.
Gọi H là trung điểm của BC, ta có\[SG \bot (ABC),G \in AH\]
Mà\[AH = \frac{{a\sqrt 3 }}{2} \Rightarrow AG = \frac{2}{3}AH = \frac{{a\sqrt 3 }}{3}\]
Tam giác SAG vuông tại G nên theo định lý Pi-ta-go ta có :
\[SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} = \sqrt {\frac{{3{b^2} - {a^2}}}{3}} = \frac{{\sqrt {9{b^2} - 3{a^2}} }}{3}\]
Đáp án cần chọn là: C
Câu 12:
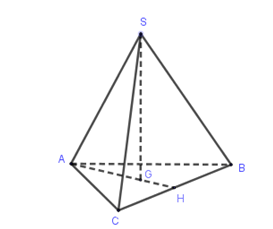
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao SH vuông góc với mp(ABCD). Gọi α là góc giữa BD và mp(SAD). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Gọi I là trung điểm \[{\rm{AS}} \Rightarrow {\rm{BI}} \bot {\rm{SA}}\]
Ta có:\[SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AD\]
Mà \[AD \bot AB\] nên \[AD \bot \left( {SAB} \right) \Rightarrow AD \bot BI\]
Suy ra\[BI \bot (SAD) \Rightarrow \alpha = \widehat {IDB}\]
Ta có: \[BI = \frac{{AB\sqrt 3 }}{2},BD = AB\sqrt 2 \Rightarrow \sin \alpha = \frac{{BI}}{{BD}} = \frac{{\sqrt 3 }}{{2\sqrt 2 }}\]
Đáp án cần chọn là: D
Câu 13:
Cho tứ diện ABCD đều. Gọi α là góc giữa AB và mp(BCD). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Gọi H là hình chiếu của A lên mp(BCD), a là độ dài cạnh của tứ diện ABCD.
Ta có\[\alpha = \widehat {ABH},BH = \frac{{a\sqrt 3 }}{3} \Rightarrow \cos \alpha = \frac{{BH}}{{AB}} = \frac{{\sqrt 3 }}{3}\]
Đáp án cần chọn là: A
Câu 14:
Cho hình thoi ABCD có tâm \(O,\widehat {ADC} = {60^0},AC = 2a\). Lấy điểm S không thuộc (ABCD) sao cho \[SO \bot (ABCD)\] Gọi \[\alpha \] là góc giữa đường thẳng SB và mặt phẳng (ABCD) và \[tan\alpha = \frac{1}{2}\]. Gọi \[\beta \] là góc giữa SC và (ABCD)(ABCD), chọn mệnh đề đúng :
 Xem đáp án
Xem đáp án
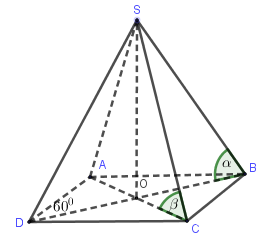
Vì \[SO \bot (ABCD)\;\] nên OB là hình chiếu của SB trên mặt phẳng đáy.
Do đó \[\alpha = \left( {SB,\left( {ABCD} \right)} \right) = \left( {SB,OB} \right) = \widehat {SBO}\] và \[\beta = \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,OC} \right) = \widehat {SCO}\] Hình thoi ABCD có \[AC = 2a,\widehat {ADC} = {60^0} \Rightarrow {\rm{\Delta }}ADC\] đều \[ \Rightarrow AD = 2a\]
Tam giác AOD vuông tại O nên \[OD = \sqrt {A{D^2} - A{O^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \Rightarrow OB = a\sqrt 3 \]
Lại có \[\tan \alpha = \frac{1}{2} \Rightarrow \frac{{SO}}{{OB}} = \frac{1}{2} \Rightarrow SO = \frac{1}{2}OB = \frac{1}{2}.a\sqrt 3 = \frac{{a\sqrt 3 }}{2}\] Vậy \[\tan \beta = \tan \widehat {SCO} = \frac{{SO}}{{OC}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{\sqrt 3 }}{2}\]
Đáp án cần chọn là: C
Câu 15:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, SA vuông góc với mặt phẳng đáy và \(SA = \sqrt {15} a\) (tham khảo hình bên)
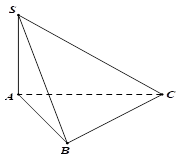
Góc giữa đường thẳng SC và mặt phẳng đáy bằng
 Xem đáp án
Xem đáp án
Bước 1:
SA vuông góc với mặt phẳng đáy nên hình chiếu của SC lên (ABC) là AC.
Bước 2:
Góc giữa SC và (ABC) là\[\widehat {SCA}\]
Bước 3:
\[\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 5 \\\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt {15} }}{{a\sqrt 5 }} = \sqrt 3 \\ \Rightarrow \widehat {SCA} = {60^0}\end{array}\]
Đáp án cần chọn là: D
Câu 16:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB, αα là góc tạo bởi đường thẳng CG và mặt phẳng (SAC). Tính \[sin\alpha .\]
 Xem đáp án
Xem đáp án
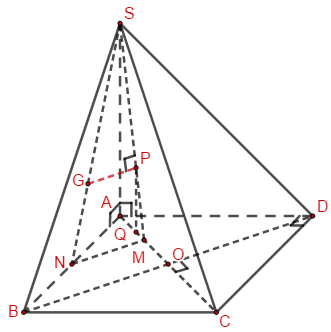
Bước 1:
Gọi O là tâm của ABCD.
M là trung điểm của AO, N là trung điểm của AB.
Qua G kẻ GP song song với MN \[(P \in SM).\]
Ta có ABCD là hình vuông nên \[BD \bot AC\]. Mà \[MN||BD \Rightarrow MN \bot AC\].
Ta lại có \[MN \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\]
\[\begin{array}{l}MN \bot \left( {SAC} \right)\\GP||MN \Rightarrow GP \bot \left( {SAC} \right)\end{array}\]
Bước 2:
Hình chiếu của C lên (SAC) là C, hình chiếu của G lên (SAC) là P.
=> Hình chiếu của CG lên (SAC) là CP
Góc giữa CG và (SAC) là góc giữa CG và CP và bằng \[\widehat {GCP} = \alpha \]
Bước 3:
\[GP = \frac{2}{3}MN = \frac{2}{3}.\frac{1}{2}OB = \frac{1}{3}.\frac{1}{2}BD = \frac{1}{6}.a\sqrt 2 \]
Kẻ\[PQ||SA \Rightarrow PQ = \frac{1}{3}SA = \frac{{2a}}{3}\]
\[\begin{array}{*{20}{l}}{CQ = \frac{1}{3}MA + 3MA = \frac{{10}}{3}.MA}\\{ = \frac{{10}}{3}.\frac{1}{4}AC = \frac{5}{6}AC = \frac{{5.a\sqrt 2 }}{6}}\\{ \Rightarrow CP = \sqrt {C{Q^2} + P{Q^2}} }\\{ = \sqrt {\frac{{25{a^2}}}{{18}} + \frac{{4{a^2}}}{9}} = a\sqrt {\frac{{11}}{6}} }\\{ \Rightarrow CG = \sqrt {C{P^2} + G{P^2}} = \frac{{a\sqrt {17} }}{3}}\\{ \Rightarrow \sin \alpha = \frac{{GP}}{{CG}} = \frac{{\sqrt 2 }}{6}.\frac{3}{{\sqrt {17} }} = \frac{1}{{\sqrt {34} }}}\end{array}\]
Đáp án cần chọn là: B
