Cường độ dòng quang điện bão hòa và hiệu suất lượng tử
-
504 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đồ thị nào dưới đây vẽ đúng đường đặc trưng Vôn - Ampe của tế bào quang điện?
Xem đáp án
Đồ thị đường đặc trưng Vôn-Ampe của tế bào quang điện:
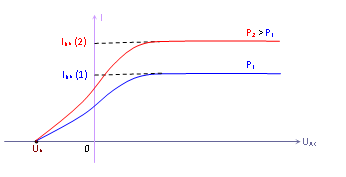
Đáp án cần chọn là: B
Câu 2:
Khi đã có dòng quang điện thì nhận định nào sau đây là sai?
Xem đáp án
A, B, D - đúng
C - sai vì cường độ dòng quang điện bão phụ thuộc vào cường độ chùm sáng kích thích
Đáp án cần chọn là: C
Câu 3:
Cường độ chùm sáng chiếu vào catốt tế bào quang điện tăng thì:
Xem đáp án
Ta có: cường độ dòng quang điện bão hòa tỉ lệ thuận với cường độ chùm sáng kích thích chiếu tới
=>Khi cường độ chùm sáng chiếu vào catốt tế bào quang điện tăng thì cường độ dòng quang điện bão hòa tăng
Đáp án cần chọn là: A
Câu 4:
Chiếu đồng thời hai bức xạ đơn sắc có bước sóng \[{\lambda _1}\] và \[{\lambda _2}\] vào một tấm kim loại. Các electron bật ra với vận tốc ban đầu cực đại lần lượt là v1và v2với \[{v_1} = 2{v_2}\;\]. Tỉ số các hiệu điện thế hãm Uh1/Uh2 để dòng quang điện triệt tiêu là:
Xem đáp án
Ta có: \[e{U_h} = \frac{1}{2}mv_{{\rm{max}}}^2\]
\[ \to \frac{{e{U_{{h_1}}}}}{{e{U_{{h_2}}}}} = \frac{{\frac{1}{2}mv_1^2}}{{\frac{1}{2}mv_2^2}} \to \frac{{{U_{{h_1}}}}}{{{U_{{h_2}}}}} = \frac{{v_1^2}}{{v_2^2}} = \frac{{4v_2^2}}{{v_2^2}} = 4\]
Đáp án cần chọn là: C
Câu 5:
Giả sử các electron đến được anốt của tế bào quang điện đều bị hút về anốt, khi đó dòng quang điện có cường độ I = 0,32mA. Số electron thoát ra khỏi catốt trong mỗi giây là:
Xem đáp án
Ta có: Cường độ dòng quang điện khi đó là dòng quang điện bão hòa:
\[{I_{bh}} = {n_e}.\left| e \right| \to {n_e} = \frac{{{I_{bh}}}}{{\left| e \right|}} = \frac{{{{0,32.10}^{ - 3}}}}{{{{1,6.10}^{ - 19}}}} = {2.10^{15}}\]
=>Số electron thoát ra khỏi catốt trong mỗi giây là ne= 2.1015
Đáp án cần chọn là: B
Câu 6:
Một đèn laze có công suất phát sáng 1W phát ánh sáng đơn sắc có bước sóng \[0,7\mu m\].
Cho \[h = {6,625.10^{ - 34}}Js,c = {3.10^8}m/s.\] Số photon của nó phát ra trong 1 giây là:
Xem đáp án
Ta có: Số photon của đèn phát ra trong 1 giây là:
\[{N_p} = \frac{{Pt}}{\varepsilon } = \frac{{P\lambda }}{{hc}}t = \frac{{{{1.0,7.10}^{ - 6}}}}{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}.1 = {3,522.10^{18}}\]
Đáp án cần chọn là: B
Câu 7:
Một hạt chuyển động có tốc độ rất lớn v = 0,6c. Nếu tốc độ của hạt tăng 4/3 lần thì động năng của hạt tăng
Xem đáp án
Khi \[v = 0,6c \Rightarrow {{\rm{W}}_d} = \left( {\frac{1}{{\sqrt {1 - \frac{{{{\left( {0,6c} \right)}^2}}}{{{c^2}}}} }} - 1} \right){m_0}{c^2} = 0,25{m_0}{c^2}\,\,\left( 1 \right)\]
Khi tốc độ của hạt tăng \[\frac{4}{3}\]lần: \[v' = \frac{4}{3}v = \frac{4}{3}.0,6c = 0,8c\]\[{{\rm{W}}_d}^\prime = \left( {\frac{1}{{\sqrt {1 - \frac{{{{\left( {0,8c} \right)}^2}}}{{{c^2}}}} }} - 1} \right){m_0}{c^2} = \frac{2}{3}{m_0}{c^2}\,\,\left( 2 \right)\]
Từ (1) và (2), ta có:
\[\frac{{{{\rm{W}}_d}^\prime }}{{{{\rm{W}}_d}}} = \frac{{\frac{2}{3}{m_0}{c^2}}}{{0,25{m_0}{c^2}}} = \frac{8}{3}\]
Đáp án cần chọn là: D
Câu 8:
Đề thi THPT QG - 2020
Giới hạn quang dẫn của CdS là \[0,9\mu m\]. Lấy \[h = {6,625.10^{ - 34}}J.s;c = {3.10^8}m/s\]. Năng lượng cần thiết để giải phóng một electron liên kết thành electron dẫn (năng lượng kích hoạt) của CdS là
Xem đáp án
Năng lượng cần thiết để giải phóng một electron liên kết thành electron dẫn:
\[\varepsilon = A = \frac{{hc}}{{{\lambda _0}}} = \frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{0,9.10}^{ - 6}}}} = {2,208.10^{ - 19}}J\]
Đáp án cần chọn là: B
Câu 9:
Một vật dao động điều hoà với phương trình \[x = 6cos(2\pi t + \frac{\pi }{6})cm.\]. Trên vật gắn với một nguồn sáng phát ánh sáng đơn sắc có tần số 5.1014Hz, công suất 0,53W. Biết hằng số Plăng là \[h = {6,625.10^{ - 34}}J.s\] Tính từ thời điểm t = 0 đến thời điểm gần nhất vật có li độ −3cm thì nguồn sáng phát số phôtôn gần nhất với giá trị nào sau đây?
Xem đáp án
Lúc t = 0,\(\left\{ {\begin{array}{*{20}{c}}{x = 3\sqrt 3 cm}\\{v < 0}\end{array}} \right.\)
Từ t = 0 đến thời điểm gần nhất vật có li độ:\(\left\{ {\begin{array}{*{20}{c}}{x = - 3cm}\\{v < 0}\end{array}} \right.\)
Khoảng thời gian vật đã đi được là: \[\frac{T}{6} + \frac{T}{{12}} = \frac{T}{4} = 0,25\left( s \right)\]
Số phôtôn gần nhất mà nguồn sáng phát ra là:
\[n = \frac{P}{{hf}}.{\rm{\Delta }}t = \frac{{0,53}}{{{{6,625.10}^{ - 34}}{{.5.10}^{14}}}}.0,25 = {4.10^{17}}\](hạt)
Đáp án cần chọn là: A
Câu 10:
Chiếu một chùm bức xạ có bước sóng \[\lambda = {\rm{ }}1800\;\mathop A\limits^0 \]vào một tấm kim loại. Các êlectrôn bắn ra có động năng cực đại bằng 6eV. Khi chiếu vào tấm kim loại đó bức xạ có bước sóng \[\lambda {\rm{ }} = {\rm{ }}5000{\rm{ }}\;\]\[\mathop A\limits^0 \] thì có hiện tượng quang điện xảy ra. Tính động năng cực đại của các êlectrôn bắn ra.
Xem đáp án
Áp dụng công thức Anhxtanh về hiện tượng quang điện ngoài
\[\begin{array}{*{20}{l}}{h\frac{c}{{{\lambda _1}}} = A + {{\rm{W}}_d} \Leftrightarrow h\frac{c}{{{{1800.10}^{ - 10}}}} = A + 6eV \Rightarrow A = h\frac{c}{{{{1800.10}^{ - 10}}}} - 6eV}\\\begin{array}{l}h\frac{c}{{{\lambda _2}}} = A + {{\rm{W}}_d} \Leftrightarrow h.\frac{c}{{{{5000.10}^{ - 10}}}} = A + {{\rm{W}}_d}\\ \Rightarrow {{\rm{W}}_d} = h.\frac{c}{{{{5000.10}^{ - 10}}}} - h\frac{c}{{{{1800.10}^{ - 10}}}} + 6eV = {2,535.10^{ - 19}}J\end{array}\end{array}\]
Đáp án cần chọn là: A
Câu 11:
Chiếu chùm ánh sáng có công suất 3W, bước sóng \[0,35\mu m\;\]vào catốt của tế bào quang điện có công thoát electron 2,48eV thì đo được cường độ dòng quang điện bão hòa là 0,02A. Hiệu suất lượng tử bằng:
Xem đáp án
Ta có: Hiệu suất lượng tử :
\[H = \frac{{{n_e}}}{{{n_p}}}100{\rm{\% }} = \frac{{{I_{bh}}.hc}}{{P\lambda e}}100{\rm{\% }} = \frac{{{{0,02.6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{3.0,35.10}^{ - 6}}{{.1,6.10}^{ - 19}}}}100{\rm{\% }} = 2,366{\rm{\% }}\]
Đáp án cần chọn là: B