Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án - đề 7
-
5270 lượt thi
-
51 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Tìm giá trị cực đại của hàm số .
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Từ đây ta có xét dấu của y' như sau: Dựa trên bảng xét dấu ta thấy hàm số đạt cực đại tại x=0 ( do y'=0 và y' đổi dấu từ dương sang âm qua x=0

Câu 4:
Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số ?
 Xem đáp án
Xem đáp án
Đáp án B
ta có xét dấu của y' như sau

Ta thấy hàm số đồng biến trên
Ta thấy hàm số nghịch biến trên (0;2)
Câu 5:
Diện tích một mặt của một hình lập phương là 9. Thể tích khối lập phương đó là
 Xem đáp án
Xem đáp án
Đáp án B
Cạnh của hình vuông:
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABCD); góc giữa hai mặt phẳng (SBC) và (ABCD) bằng Khi đó khối chóp S.ABC có thể tích là
 Xem đáp án
Xem đáp án
Đáp án B
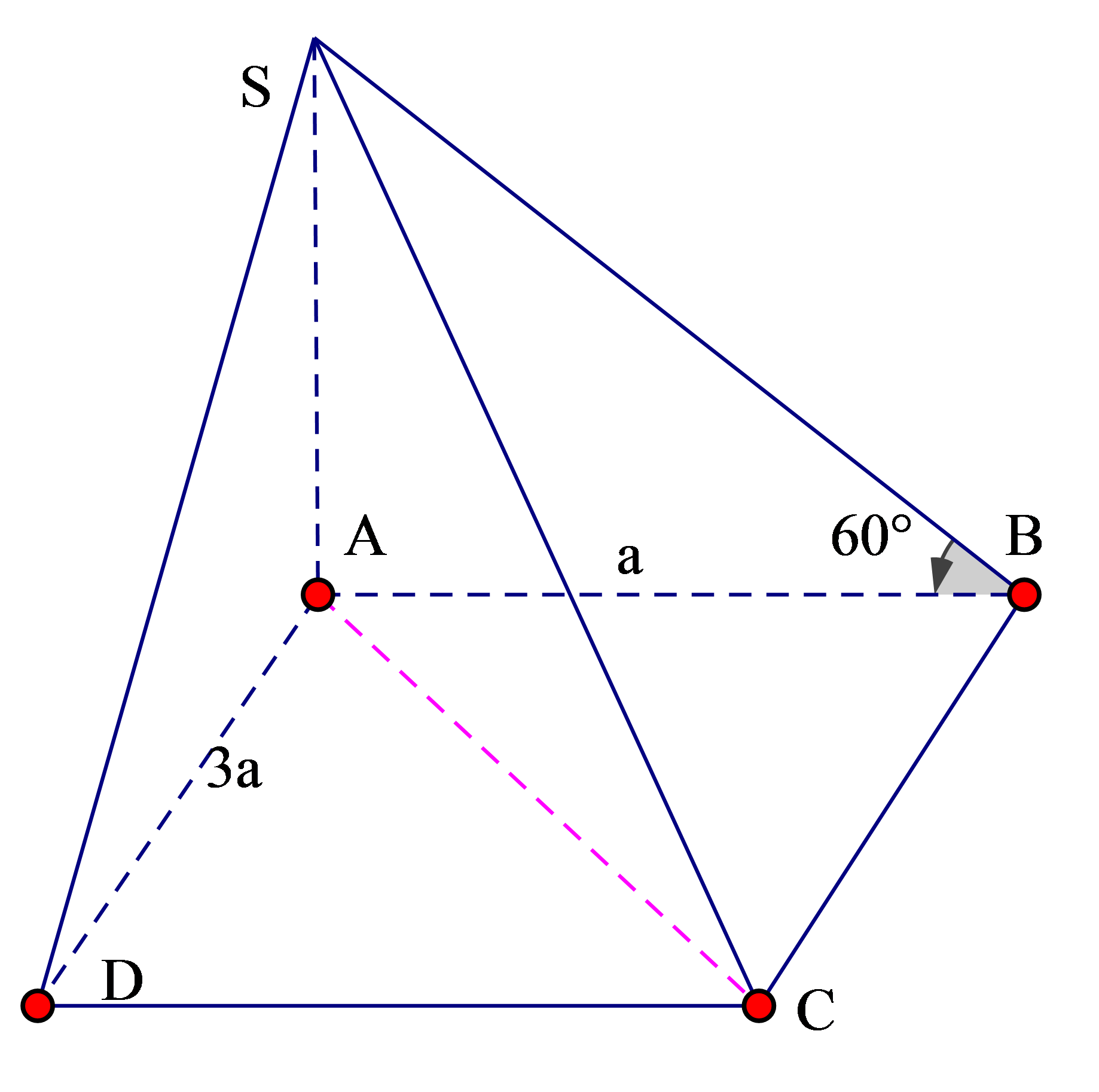
Vì (SAB),(SAC) cùng vuông góc với (ABCD) nên giao tuyến
Do AB, SB cùng vuông góc với giao tuyến BC của (ABCD) và (SBC) nên góc giữa hai mặt phẳng trên là góc:
Vậy:
Câu 7:
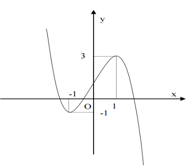
Cho hàm số y=f(x) có đồ thị như hình vẽ bên, trong các khẳng định sau khẳng đinh nào là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Đây là hàm số bậc ba nên không có giá trị lớn nhất và nhỏ nhất nên đáp án A sai
Hàm số có GTCD =3 nên đáp án B sai
Hàm số đạt cực cực tiều tại x=-1 , đạt cực đại tại x=1 nên đáp án C sai.
Đáp án D đúng vì đồ thị hàm số có điểm cực tiểu A(-1;1) và điểm cực đại B(1;3).
Câu 8:
Vào 4 năm trước, chị Thương có gửi vào ngân hàng một số tiền là 20 triệu đồng theo hình thức lãi kép có kỳ hạn. Số tiền hiện tại chị nhận được là 29,186792 triệu đồng. Biết rằng, lãi suất ngân hàng tại thời điểm mà chị Thương gửi tiền là 0,8 %/tháng. Hỏi kỳ hạn ![]() mà chị Thương đã chọn là bao nhiêu tháng?
mà chị Thương đã chọn là bao nhiêu tháng?
 Xem đáp án
Xem đáp án
Đáp án C
Sau 4 năm số tiền chị Thương nhận được là:
Kiểm tra các giá trị của k trong đáp án ta thấy đẳng thức đúng với k=4
Câu 11:
Cho hàm số có đạo hàm .
Tìm số điểm cực trị của hàm số .
 Xem đáp án
Xem đáp án
Đáp án A
Ta thấy nhưng y' chỉ đổi dấu qua và y' không đổi dấu qua x=-1 nên hàm số có hai cực trị.
Câu 13:
Đồ thị hàm số có số giao điểm với trục Ox là:
 Xem đáp án
Xem đáp án
Đáp án C
Số giao điểm của đồ thị hàm số với trục Ox là số nghiệm của PT:
như vậy số giao điểm là 3.
Câu 15:
Cho hàm số . Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Đáp án C
đồ thị hàm số có tiệm cận đứng x=2
đồ thị hàm số có tiệm cận ngang y=-1
Câu 16:
Nhận xét nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Log của tích các số dương thì bẳng tổng các log thành phần.
Câu 17:
Cho hàm số . Khẳng định nào sau đây là đúng.
 Xem đáp án
Xem đáp án
Đáp án B
Ta có với => Hàm số nghịch biến trên mỗi khoảng và ( chú ý: Đáp án A đưa ra tập biểu diễn đúng nhưng sai về mặt ngôn ngữ vì không được gọi là một khoảng)
Câu 19:
Đường thẳng có phương trình cắt đồ thị của hàm số tại hai điểm A và B với tọa độ được kí hiệu lần lượt là và trong đó . Tìm ?
 Xem đáp án
Xem đáp án
Đáp án A
Hoành độ giao điểm của đường thẳng có phương trình và đồ thị của hàm số là nghiệm PT:
Câu 20:
Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 0.
 Xem đáp án
Xem đáp án
Đáp án C
Ta có: và ; PTTT tại điểm của đồ thị hàm số là:
Vậy PTTT tại là:
Câu 21:
Tìm giá trị lớn nhất của hàm số trên đoạn .
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Vậy GTLN của hàm số đã cho trên là:
Câu 22:
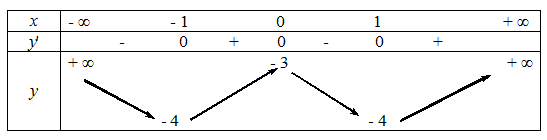
Bảng biên thiên dưới đây là của hàm số nào?
 Xem đáp án
Xem đáp án
Đáp án A
Dựa trên bảng biến thiên ta thấy:
Tận cùng bên phải hàm số cùng dấu với hệ số của nên ta loại đáp án B
Tại x=0 thì y=-3 nên ta loại đáp án D
Tại x=1 thì y=-4 nên ta loại đáp án C và chọn đáp án A
Câu 23:
Cho hàm số .Điểm nào sau đây thuộc đồ thị hàm số?
 Xem đáp án
Xem đáp án
Đáp án D
Dễ thẫy khi nên đồ thị hàm số
Câu 24:
Một hình lăng trụ có 2017 mặt. Hỏi hình lăng trụ đó có bao nhiêu cạnh
 Xem đáp án
Xem đáp án
Đáp án D
Hình lăng trụ có 2017 mặt thì có 2015 mặt bên => có 2015 cạnh bên.
Số cạnh của hình lăng trụ bằng ba lần số cạnh bên tức là bằng 2015.3=6045
Câu 27:
Hàm số nào sau đây không có cực trị?
 Xem đáp án
Xem đáp án
Đáp án B
Hàm số bậc nhất chia bậc nhất luôn đồng biến hoặc nghich biến trên tập xác định của nó do vậy không có cực trị.
Cụ thể ở đây với do vậy hàm số ở đáp án B luôn nghịch biến hay nó không có cực trị.
Câu 28:
Nghiệm dương bé nhất của phương trình: là:
 Xem đáp án
Xem đáp án
Đáp án A
PT:
Như vậy nghiệm dương bé nhất của PT đã cho là ứng với của nghiệm (1)
Câu 29:
Tất cả các tiệm cận ngang của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
và
=> hàm số đã cho có hai tiệm cận ngang ![]()
Câu 30:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA=a.Tính thể tích khối chóp S.ABC.
 Xem đáp án
Xem đáp án
Đáp án C
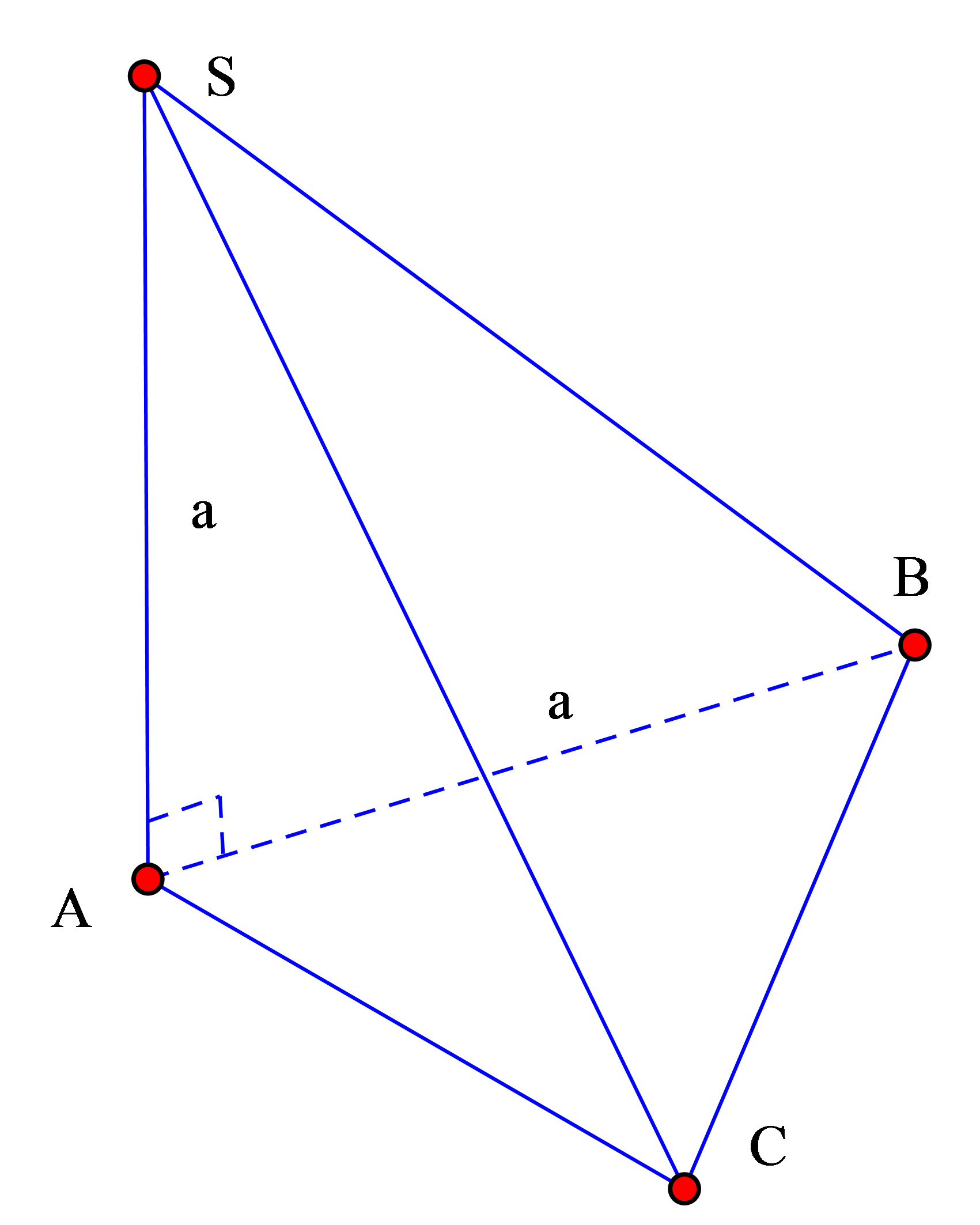
Ta có diện tích tam giác đều cạnh a là
Câu 31:
Tìm m để bất phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Đáp án B
Bất PT:
Đặt ta được BPT ;
Như vậy bài toán trở thành tìm để BPT (1) có nghiệm
Như vậy ta chọn đáp án B do
Câu 32:
Có bao nhiêu số tự nhiên gồm 7 chữ số thỏa mãn số đó có 3 số chữ chẵn và số đứng sau lớn hơn số đứng trước.
 Xem đáp án
Xem đáp án
Đáp án B
Mỗi số thỏa mãn điều kiện bài toán gồm 3 số chẵn và 4 số lẻ, do sắp xếp từ bé đến lớn nên với 7 số chọn ra chỉ có duy nhất một cách sắp xếp.
+) Số cách chọn ra 3 số chẵn từ 5 số chẵn là:
+) Số cách chọn ra 4 số lẻ từ 5 số chẵn là:
Vậy tổng số các chữ số thỏa mãn điều kiện bài toán là:
Câu 33:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy , , . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
 Xem đáp án
Xem đáp án
Đáp án A
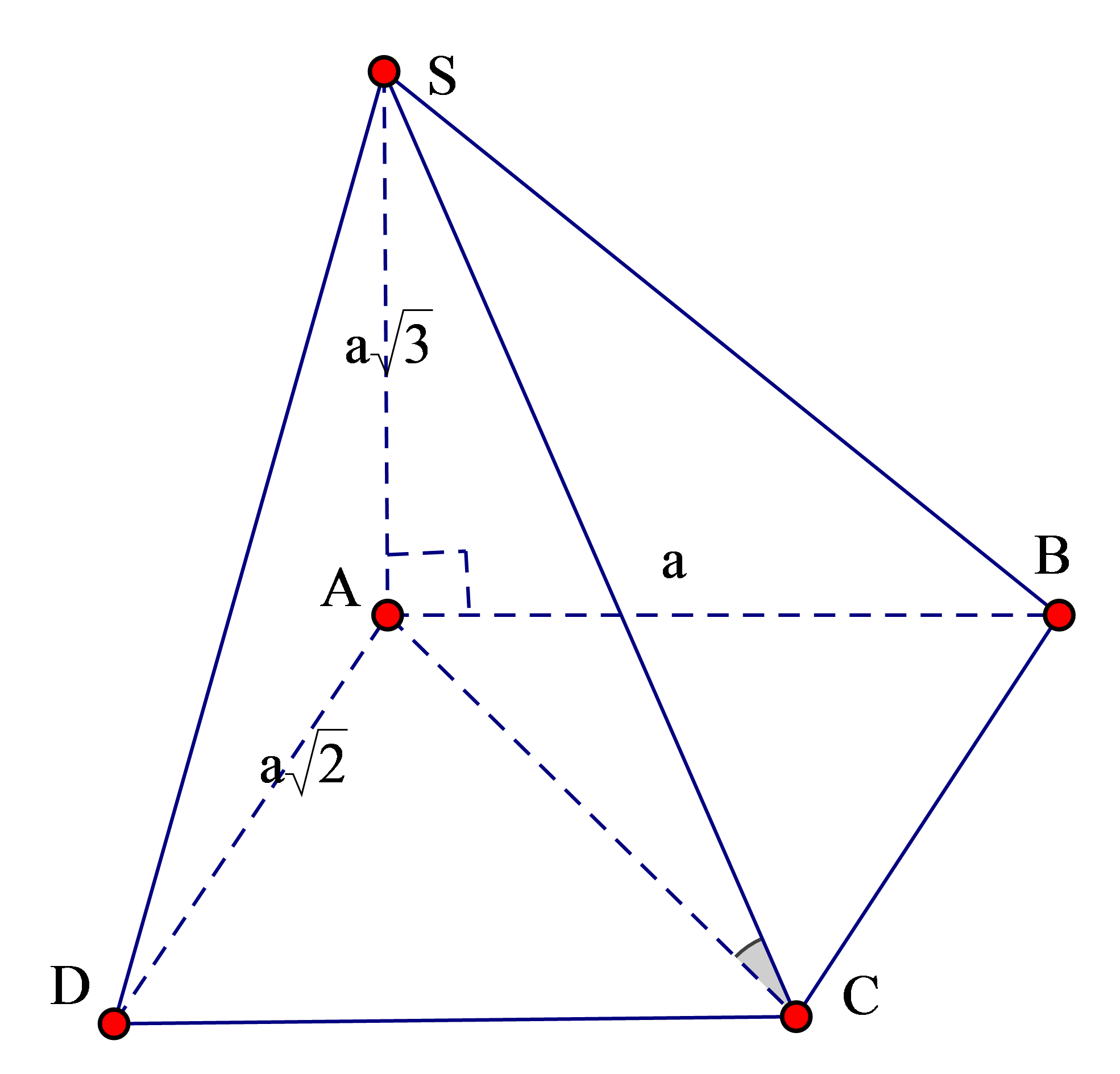
Góc giữa mặt phẳng và đường thẳng là góc tạo bởi đường thẳng đó với hình chiếu của nó lên mặt phẳng. Ở đây góc là góc giữa Sc và (ABCD)
Ta có:
Câu 34:
Trong mặt phẳng với hệ tọa độ Oxy, cho parabol và parabol (P') là ảnh của (P) qua phép tịnh tiến theo , với 0<b<4. Gọi A,B là giao điểm của (P) với Ox, M,N là giao điểm của (P') với Ox , I, J lần lượt là đỉnh của (P) và (P'). Tìm tọa độ điểm J để diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN.
 Xem đáp án
Xem đáp án
Đáp án D
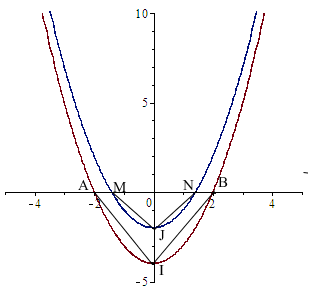
Phép tịnh tiến theo biến parabol thành parabol
Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là:
Giao điểm M,N với Ox của (P) có toạn độ lần lượt là:
Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt:
Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:
Câu 35:
Tìm ảnh của đường tròn qua phép tịnh tiến theo vectơ .
 Xem đáp án
Xem đáp án
Đáp án D
Phép tịnh tiến theo biến tâm của đường tròn (C) thành tâm của đường tròn (C') có cùng bán kính.
Vậy ảnh của đường tròn (C) qua phép tịnh tiến theo là đường tròn (C')có PT là:
Câu 36:
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d' có phương trình là ảnh của đường thẳng d có phương trình qua phép tịnh tiến theo vectơ . Tìm tọa độ vectơ có độ dài bé nhất.
 Xem đáp án
Xem đáp án
Đáp án B
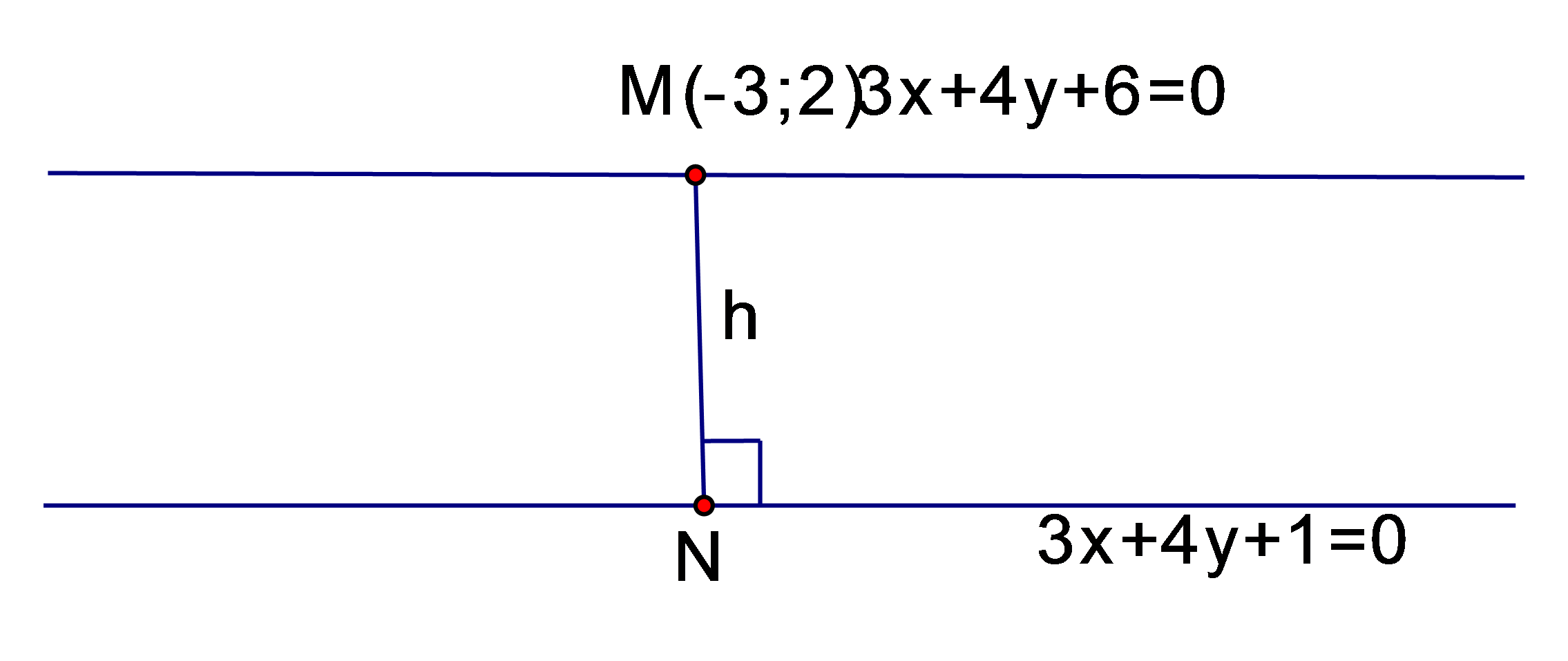
Độ dài véc tơ bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ tới sao cho trong đó là VTCP của cả d và d' .Và khi đó:
Chọn . Ta cần tìm sao cho:
Câu 37:
Cho hình chóp S.ABC có độ dài các cạnh: thỏa mãn . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.
 Xem đáp án
Xem đáp án
Đáp án C
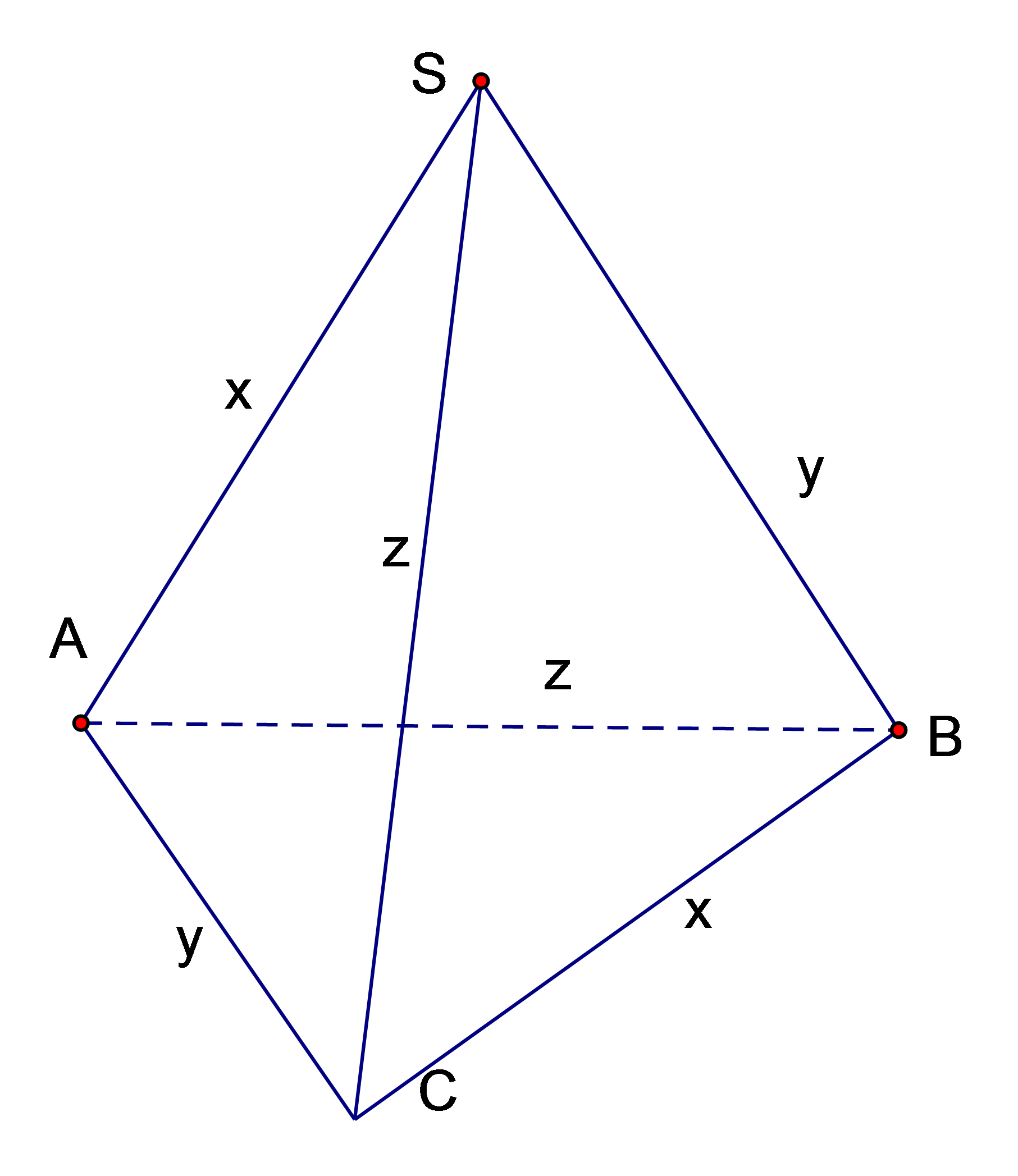
Áp dụng công thức tính thể tích tứ diện có hai cặp cạnh đối bằng nhau:
Như vậy lớn nhất bằng khi: x=y=z=2
Câu 38:
Số các giá trị nguyên của của m để hàm số đồng biến trên mỗi khoảng xác định là
 Xem đáp án
Xem đáp án
Đáp án A
Ta có: để hàm số đồng biến trên mỗi khoảng xác định của nó thì điều kiện cần và đủ là:
Vậy các giá trị nguyên của m thỏa mãn điều kiện là:
Câu 39:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy, góc giữa cạnh SB và mặt đáy bằng . Độ dài cạnh SC bằng
 Xem đáp án
Xem đáp án
Đáp án C
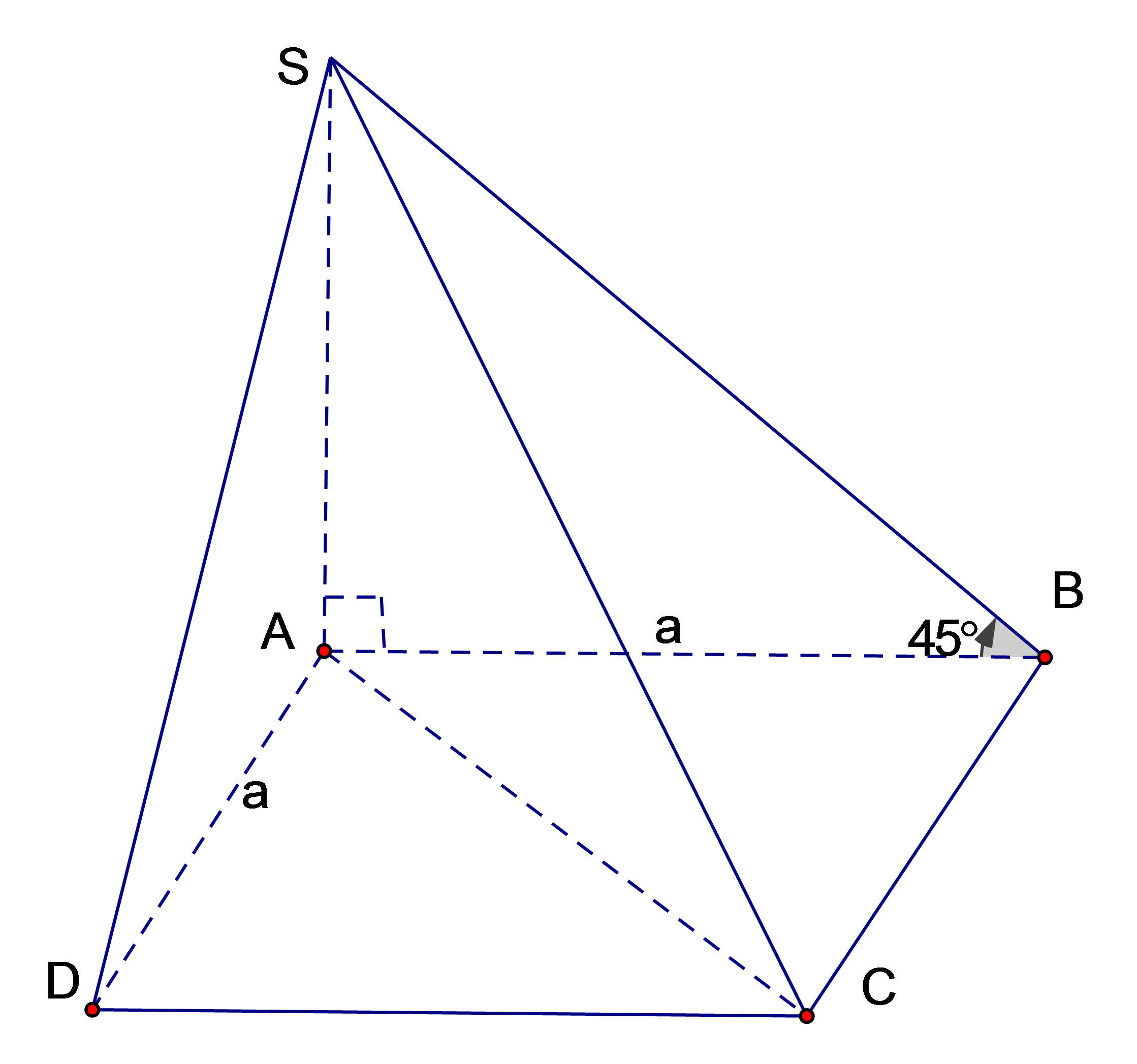
Do nên góc giữa SB với (ABCD) là góc
=> vuông cân tại A ;
ta có:
Vậy
Câu 40:
Tìm m để phương trình có 4 nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Đáp án C
Xét hàm số có:
Ta có bảng biến thiên của như sau:
Từ bảng biến thiên này ta có bang biến thiên của như sau:
Dựa trên bảng biến thiên này ta thấy PT:
có 4 nghiệm phân biệt
Câu 41:
Tìm hệ số của số hạng không chứa x trong khai triển . Biết có đẳng thức là:
 Xem đáp án
Xem đáp án
Đáp án C
Ta có: nên đẳng thức:
Số hạng tổng quát trong khai triển: là:
Số hạng không chứa x ứng với k thỏa mãn:
và có giá trị là:
Câu 42:
Cho khối lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng . Tính thể tích của khối lăng trụ .
 Xem đáp án
Xem đáp án
Đáp án B

Gọi M là trung điểm BC kẻ đường cao Ah trong . Khi đó AH là khoảng cách từ A tới .
AM là đường cao trong tam giác đều ,
Ta có
Vậy
Câu 43:
Cho khối lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng . Tính thể tích của khối lăng trụ .
 Xem đáp án
Xem đáp án
Đáp án B

Gọi M là trung điểm BC, kẻ đường cao AH trong . Khi đó AH là khoảng cách từ A tới .
AM là đường cao trong tam giác đều ,
Ta có:
Câu 44:
Đồ thị hàm số có tọa độ điểm cực tiểu là . Khi đó m+n bằng
 Xem đáp án
Xem đáp án
Đáp án A
Ta có: hàm số có cực tiểu là:
=> nghiệm lớn của PT y'=0 là 1
Do y'=0 nếu có hai nghiệm thì hai nghiệm cùng dấu
Khi đó
vậy:
Câu 45:
Bất phương trình:
có tập nghiệm là . Giá trị của 2a+b là
 Xem đáp án
Xem đáp án
Đáp án A
Điều kiện: ta có hệ phương trình:
nên ta có lập luận sau
Vế phải bất phương trình:
+) Với x>1 thì:
Vật tập nghiệm của bất phương trình là:
Câu 46:
Tìm m để hàm số:
đạt cực trị tại 2 điểm thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
hàm số đã cho luôn có hai cực trị tại thõa mãn:
Ta biến đổi PT:
Câu 47:
Trong một kì thi. Thí sinh được phép thi 3 lần. Xác suất lần đầu vượt qua kì thi là 0,9. Nếu trượt lần đầu thì xác suất vượt qua kì thi lần hai là 0,7. Nếu trượt cả hai lần thì xác suất vượt qua kì thi ở lần thứ ba là 0,3. Xác suất để thí sinh thi đậu là
 Xem đáp án
Xem đáp án
Đáp án D
Để thi đậu thí sinh có thể vượt qua kì thi ở một trong 3 vòng.
Xác suất thí sinh đậu vòng 1 là:
Xác suất thí sinh đậu vòng 2 là:
Xác suất thí sinh đậu vòng 3 là:
Vậy xác suất thí sinh đậu kì thi là:
Câu 48:
Khối lăng trụ đều ABCD.A’B’C’D’ có thể tích . Tính thể tích V của khối tứ diện ACB’D’.
 Xem đáp án
Xem đáp án
Đáp án A
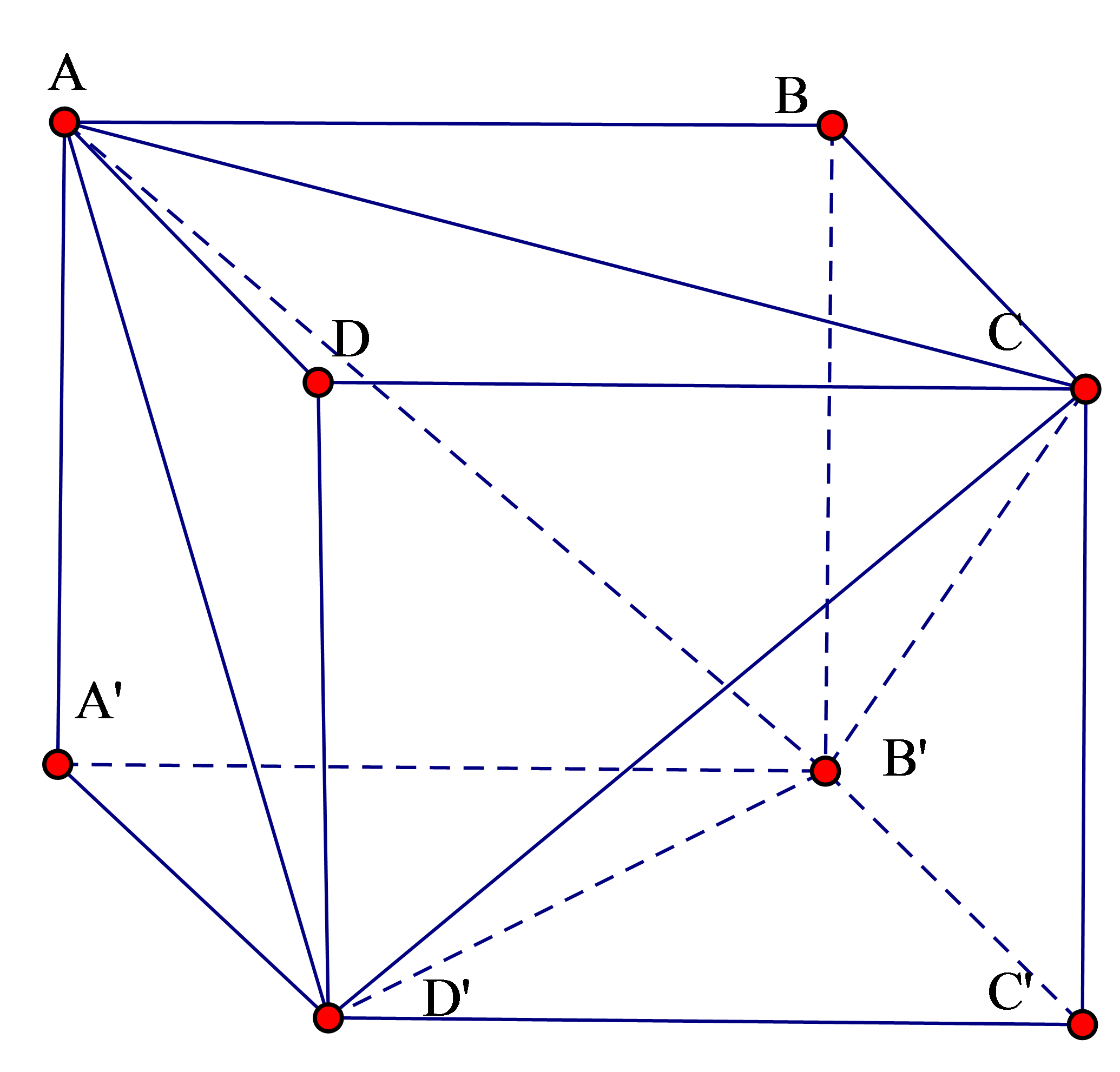
Gọi độ dài cạnh đáy là a, độ dài cạnh bên là b ta có:
Tứ diện ACB'D' có các cặp đối bằng nhau
Áp dung công thức tính thể tích của tứ diện có các cặp đối bằng nhau ta có:
(Do tính đối xứng ta có thể tính:
)
Câu 49:
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
Vậy hàm số . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
do điểm tiếp xúc có hoành độ dương
=> => f(x) cắt trục tung tại điểm có tung độ
Câu 50:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh AB = 2a . Tam giác SAB là tam giác đều và nằm trong mặt phắng vuông góc với đáy. Gọi M là trung điểm SB và N là điểm trên cạnh SC sao cho SC=3SN. Tính thể tích V của khối chóp S.AMN.
 Xem đáp án
Xem đáp án
Đáp án B
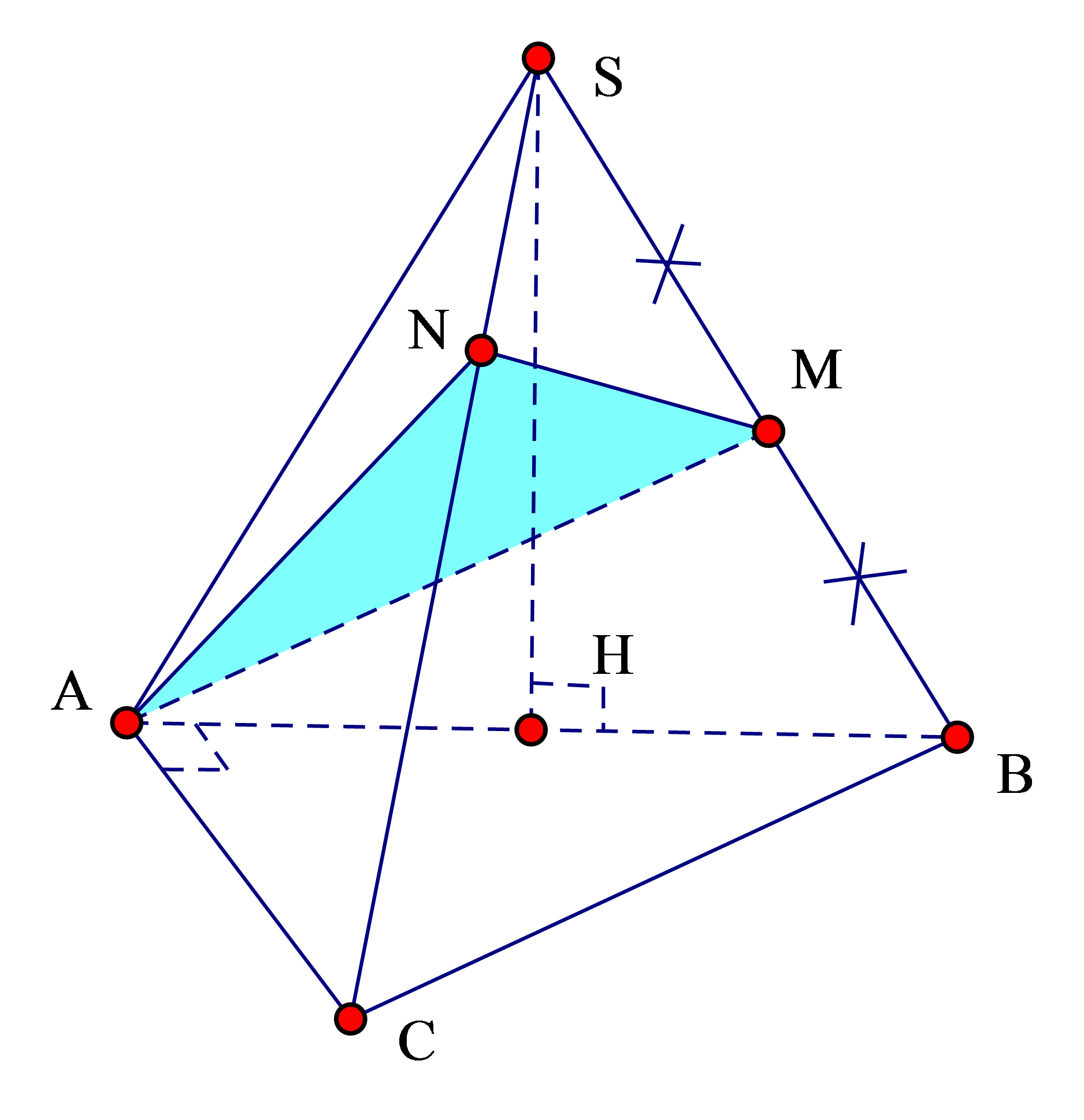
Kẻ đường cao SH trong .
đều
Diện tích tam giác:
Ta có:
Câu 51:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc có SO vuông góc mặt phẳng (ABCD) và SO = a, Khoảng cách từ O đến mặt phẳng (SBC) là
 Xem đáp án
Xem đáp án
Đáp án C
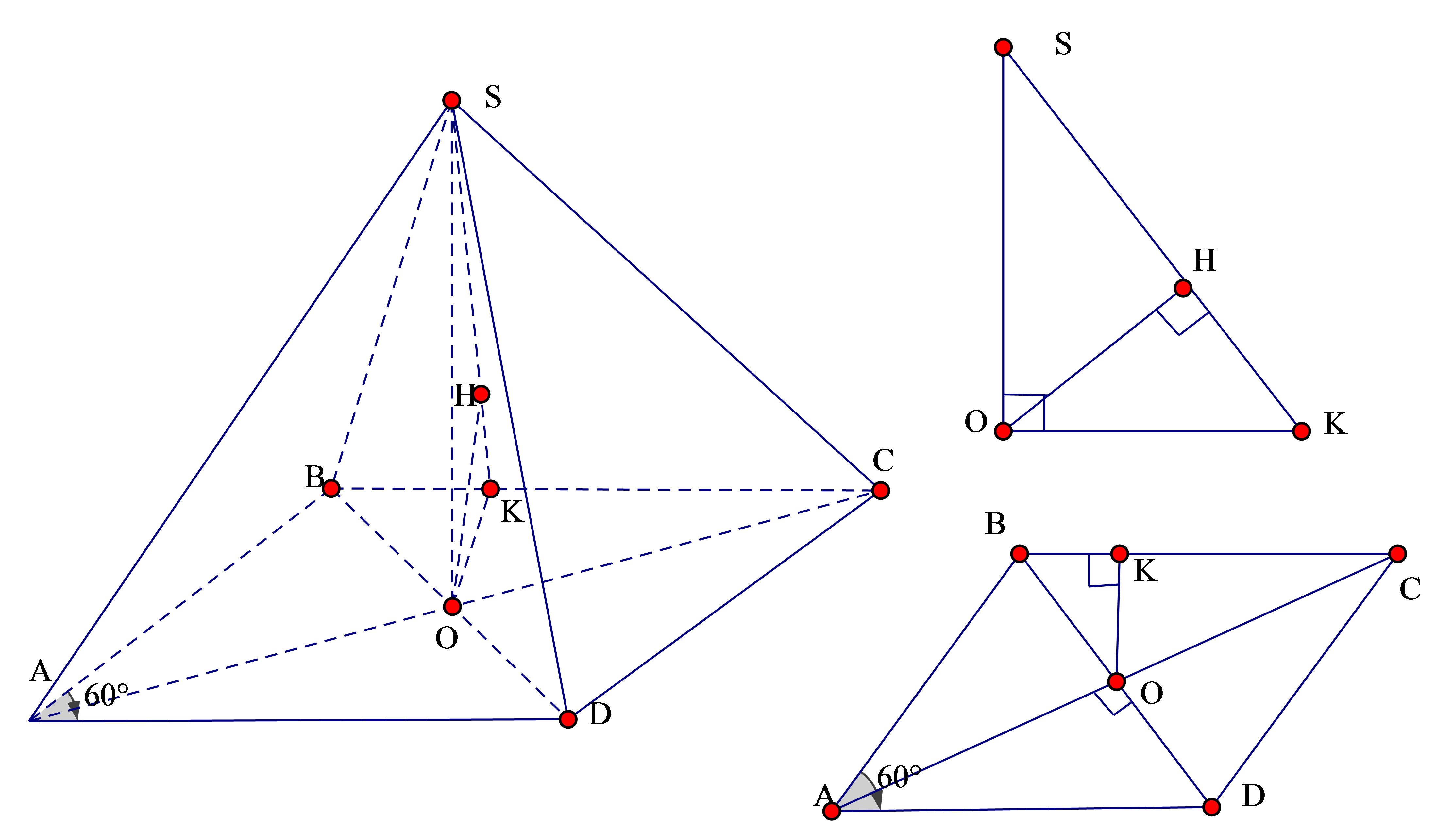
Kẻ như hình vẽ khi đó OH là khoảng cách từ O tới (SBC)
Dễ thấy đều
Ta có:
