Trắc nghiệm Biểu đồ. Số trung bình cộng có đáp án (Vận dụng)
-
2249 lượt thi
-
10 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
Khối lượng của 40 con lợn được chọn ngẫu nhiên trong lô thử nghiệm (theo phương pháp khoa học) và lô đối chứng (theo phương pháp cũ) được làm tròn đến kg như sau:
Lô thử nghiệm
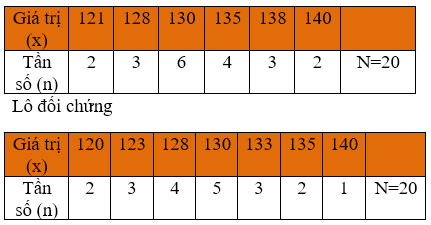
Chọn đáp án đúng nhất để điền vào chỗ trống trong khẳng định sau:
Trọng lượng trung bình mỗi con lợn ở lô thử nghiệm so với lô đối chứng _____
 Xem đáp án
Xem đáp án
Hướng dẫn:
Tính số trung bình cộng trọng lượng của mỗi con lợn ở từng lô, sau đó so sánh.
Bài giải:
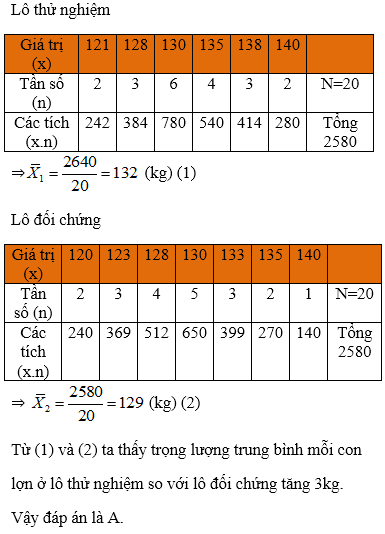
Câu 2:
Trung bình cộng của 24 số là 15. Nếu loại đi hai số 20 và 21 thì trung bình cộng của các số còn lại bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Hướng dẫn:
Tính tổng của 22 số còn lại (sau khi bỏ hai số 20 và 21)
Tính số trung bình của 22 số còn lại đó.
Bài giải:
Trung bình cộng của 24 số là 15 thì tổng của 24 số là:
24 . 15 = 360
Tổng của 22 số (sau khi loại hai số 20 và 21) là:
360 – 20 – 21 = 319
Số trung bình cộng của 22 số còn lại là:
Vậy số cần điền vào ô trống là 14,5
Câu 3:
Học sinh lớp 7A trường Trung học cơ sở Nguyễn Trãi được phân loại về học lực như sau: 20% loại giỏi, 25% loại khá, 50% loại trung bình, 5% loại yếu.
Ta có biểu đồ hình quạt biểu diễn sự phân loại theo dữ kiện trên là:
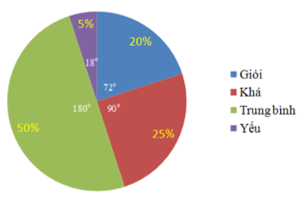
 Xem đáp án
Xem đáp án
Hướng dẫn:
Ta kiểm tra các vấn đề sau:
- Các vùng đánh dấu số phần trăm xếp loại học lực của học sinh trong biểu đồ có đúng không.
- Số đo góc ở tâm có tương ứng với số phần trăm xếp loại học lực không.
Bài giải:
Từ số liệu đã cho, ta có thể biểu diễn bằng biểu đồ hình quạt như sau:
- Dựng hình tròn có bán kính tự chọn
- Hình tròn này được chia thành các hình quạt mà góc ở tâm của hình quạt tỉ lệ với tần suất (phần trăm loại học sinh)
20% loại giỏi thì góc ở tâm là:
Tương tự, 25% loại khá thì góc ở tâm là:
50% loại trung bình thì góc ở tâm là:
5% loại yếu thì góc ở tâm là:
Do đó, biểu đồ hình quạt trong đề bài hoàn toàn đúng với số liệu đã cho.
Vậy đáp án là Đúng.
Lưu ý: Đối với các bài vẽ biểu đồ hình quạt với các số liệu đã cho trước, ta làm như sau:
+ Dựng hình tròn có bán kính tự chọn
+ Xác định số phần trăm của từng đối tượng được xét
+ Tính số đo góc ở tâm theo từng số phần trăm của từng đối tượng đó.
Công thức tính góc ở tâm như sau: (Số phần trăm) ×
Câu 4:
Một bảng số liệu điều tra có 20 giá trị. Nếu mỗi giá trị của dấu hiệu tăng thêm 2 đơn vị thì số trung bình cộng của dấu hiệu đó tăng thêm bao nhiêu đơn vị?
 Xem đáp án
Xem đáp án
Hướng dẫn:
Viết công thức tính số trung bình cộng của 20 giá trị dạng tổng quát.
Sau đó thêm mỗi giá trị 2 đơn vị và tính số trung bình mới.
So sánh số trung bình cũ và số trung bình mới
Bài giải:
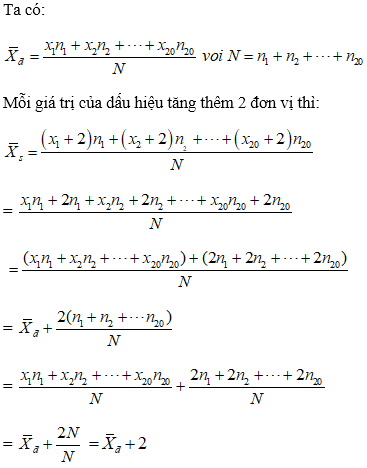
⇒ Số trung bình cộng lúc sau tăng 2 đơn vị so với số trung bình cộng lúc đầu.
Vậy đáp án là B.
Câu 5:
Khẳng định sau đây Đúng hay Sai?
Nếu nhân mỗi giá trị của dấu hiệu với một hằng số thì số trung bình cộng của dấu hiệu cũng nhân lên với hằng số đó.
 Xem đáp án
Xem đáp án
Hướng dẫn:
Viết công thức tính số trung bình cộng của dấu hiệu dạng tổng quát.
Sau đó nhân mỗi giá trị với hằng số a và tính số trung bình mới.
Bài giải:

Câu 6:
Một trường THCS có 40 thầy cô giáo, tuổi trung bình là 42,1. Sang năm học mới, có một thầy giáo 60 tuổi và một cô giáo 55 tuổi nghỉ hưu. Nhà trường nhận thêm một cô giáo 21 tuổi và một thầy giáo 22 tuổi. Tuổi trung bình của các thầy cô giáo của trường trong năm học mới là:
 Xem đáp án
Xem đáp án
Hướng dẫn:
Tính tổng tuổi của 40 thầy cô giáo lúc đầu.
Tính tổng tuổi của các thầy cô giáo sau khi có sự thay đổi khi sang năm học mới.
Bài giải:
Tổng tuổi của 40 thầy cô giáo của trường lúc đầu là:
42,1 . 40 = 1684 (tuổi)
Sang năm học mới, tổng tuổi của các thầy cô của trường (sau khi có sự luân chuyển) là:
1684 – 60 – 55 + 21 + 22 = 1612 (tuổi)
Tuổi trung bình của các thầy cố giáo của trường trong năm học mới là:
(tuổi)
Vậy đáp án là D.
Câu 7:
Tám đội bóng tham gia một giải bóng đá. Mỗi đội đều phải đá với mỗi đội khác
Toàn giải có số trận đấu là
một trận lượt đi, một trận lượt về.
 Xem đáp án
Xem đáp án
Nếu gọi các đội lần lượt là đội 1,..., đội 8.
Một đội đá với 7 đội còn lại là 7 trận.
Vì có tất cả 8 đội nên cả giải đấu có: 7 . 8 = 56 (trận)
(Trong đó mỗi đội đã đá với một đội khác hai trận là trận lượt đi và trận lượt về)
Vậy số cần điền vào ô trống là 56.
Cách khác:
Đội thứ nhất phải đá với 7 đội còn lại (cả lượt đi và lượt về) nên có 14 trận.
Vì số trận của đội thứ hai đá với đội thứ nhất là 2 trận, đã được tính nên đội này chỉ còn đá 12 trận.
Đội thứ 3 đã đá với đội thứ nhất và thứ hai nên chỉ còn đá 10 trận.
Tiếp tục quá trình lập luận đó ta có số trận của các đội thứ tư, thứ năm….., thứ tám chỉ còn là: 8 trận, 6 trận, …., 0 trận
Toàn giải có số trận đấu là:
14 + 12 + 10 + 8 + 6 + 4 + 2 + 0 = 56(trận)
Câu 8:
Tám đội bóng tham gia một giải bóng đá. Mỗi đội đều phải đá với mỗi đội khác một trận lượt đi, một trận lượt về.
Ta có bảng về số bàn thắng trong mỗi trận và tần số của nó như sau:
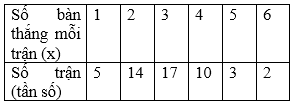
Số bàn thắng trung bình của mỗi trận là:
 Xem đáp án
Xem đáp án
Theo câu 1, ta đã biết số trận đấu của cả giải đấu là: 56 (trận).
Số bàn thắng trung bình của mỗi trận là:
≈ 2,7 (bàn)
Vậy đáp án là B.
Câu 9:
Một học sinh viết 27 số rồi tính trung bình của chúng, nhưng sau đó lại viết tiếp số trung bình cộng đó bên cạnh rồi tính luôn số trung bình cộng của 28 số. Số trung bình cộng lúc sau lớn hơn, nhỏ hơn hay bằng số trung bình cộng lúc đầu (trung bình cộng của 27 số).
 Xem đáp án
Xem đáp án
Hướng dẫn:
Gọi trung bình cộng của 27 số lúc đầu là a
Tìm tổng của 27 số lúc đầu theo a
Tính trung bình cộng lúc sau theo a.
Bài giải:
Gọi số trung bình cộng lúc đầu (trung bình cộng của 27 số) là a.
Tổng của 27 số là: 27a
Số trung bình cộng lúc sau là:
⇒ Số trung bình cộng lúc sau bằng số trung bình cộng lúc đầu.
Vậy đáp án là C.