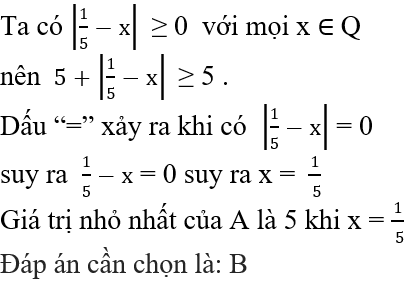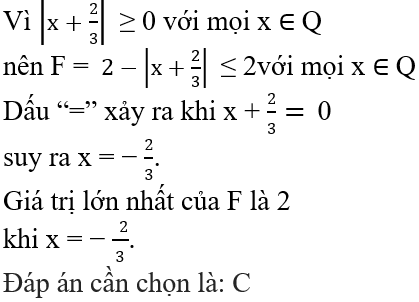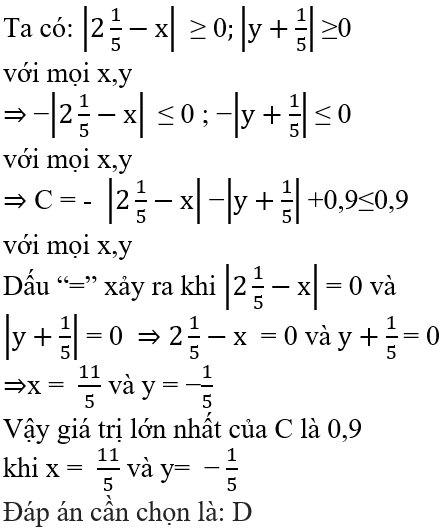Trắc nghiệm giá trị tuyệt đối của một số hữu tỉ có đáp án (Vận dụng)
-
1905 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 4:
Giá trị nhỏ nhất của biểu thức là:
Xem đáp án
Ta có: |2x−0,4| ≥ 0 với mọi x ∈ Q nên |2x−0,4| − ≥ − với mọi x ∈ Q .
Dấu “=” xảy ra khi |2x−0,4| = 0 ⇒ 2x−0,4 = 0 ⇒ 2x = 0,4 ⇒ x = 0,2.
Giá trị nhỏ nhất của A là: − khi x = 0,2
Đáp án cần chọn là: B
Câu 6:
Biểu thức F = đạt giá trị lớn nhất khi x bằng:
Xem đáp án
Ta có: |x−7,8| ≥ 0 với mọi x ∈ Q
⇒ −2|x−7,8 | ≤ 0 với mọi x ∈ Q
⇒ F=22,5 − 2|x−7,8| ≤ 22,5 với mọi x ∈ Q
Dấu “=” xảy ra khi |x−7,8| = 0⇒ x− 7,8 = 0 ⇒ x = 7,8
Giá trị lớn nhất của F là 22,5 khi x = 7,8.
Đáp án cần chọn là: A
Câu 7:
Với giá trị nào của x,y thì biểu thức C = 4- đạt giá trị lớn nhất?
Xem đáp án
Vì |5x−5| ≥ 0 ; 3y+12| ≥ 0 với mọi x,y nên
C = 4−|5x−5|−|3y+12| ≤ 4 với mọi x,y
Dấu “=” xảy ra khi 5x−5 = 0 và 3y+12 = 0 suy ra x = 1và y = −4.
Vậy giá trị lớn nhất của C là 4 khi x = 1 ; y = −4.
Đáp án cần chọn là: D
Câu 9:
Có bao nhiêu gía trị của x thỏa mãn ?
Xem đáp án
Vì |x−3,5| ≥ 0 ; |x−1,3| ≥ 0 với mọi x nên |x−3,5| + |x−1,3| ≥ 0 với mọi x.
Để |x−3,5| + |x−1,3| = 0 thì x−3,5 = 0 và x−1,3 = 0 suy ra x = 3,5 và x = 1,3 (vô lý vì x không thể đồng thời nhận cả hai giá trị).
Không có giá trị nào của x thỏa mãn đề bài.
Đáp án cần chọn là: D
Câu 10:
Có bao nhiêu giá trị của x thỏa mãn ?
Xem đáp án
Vì |2x−5| ≥ 0 ; |5,7−x| ≥ 0 với mọi x nên |2x−5| + |5,7−x| ≥ 0 với mọi x.
Mặt khác |2x−5| + |5,7−x| ≤ 0
Do đó |2x−5|+|5,7−x| = 0
Khi đó 2x−5 = 0 và 5,7−x = 0 suy ra x = và x = 5,7 (vô lý vì x không thể đồng thời nhận cả hai giá trị).
Vậy không có giá trị nào của x thỏa mãn đề bài.
Đáp án cần chọn là: D
Câu 13:
Rút gọn biểu thức khi x < -0,8
Xem đáp án
Ta có: x < −0,8hay x+0,8 < 0nên |x+0,8| = −(x+0,8) = −x−0,8
Vì x <− 0,8nên x−2,5 < 0. Do đó |x−2,5|= − (x−2,5)= −x+2,5
Khi đó A = |x+0,8| − |x−2,5|+1,9
= −x−0,8−(−x+2,5)+1,9
= −x−0,8+x−2,5+1,9
= (−x+x)−(0,8+2,5−1,9)
= −(0,8+2,5−1,9)
= −1,4
Đáp án cần chọn là: A